You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.1
Question 1.

Solution:
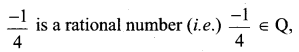
3.14 ∈ Q
0, 4 are integers and 0 ∈ Z, 4 ∈ N, Z, Q
\(\frac{22}{7} \in \mathrm{Q}\)
![]()
Question 2.
Prove that \(\sqrt{3}\) is an irrational number.
(Hint: Follow the method that we have used to prove \(\sqrt{2}\) ∉ Q.
Solution:
Suppose that \(\sqrt{3}\) is rational P

⇒ 3 is a factor of q also
so 3 is a factor ofp and q which is a contradiction.
⇒ \(\sqrt{3}\) is not a rational number
⇒ \(\sqrt{3}\) is an irrational number
Question 3.
Are there two distinct irrational numbers such that their difference is a rational number? Justify.
Solution:
Taking two irrational numbers as 3 + \(\sqrt{2}\) and 1 + \(\sqrt{2}\)
Their difference is a rational number. But if we take two irrational numbers as 2 – \(\sqrt{3}\) and 4 + \(\sqrt{7}\).
Their difference is again an irrational number. So unless we know the two irrational numbers we cannot say that their difference is a rational number or irrational number.
![]()
Question 4.
Find two irrational numbers such that their sum is a rational number. Can you find two irrational numbers whose product is a rational number.
Solution:
(i) Let the two irrational numbers as 2 + \(\sqrt{3}\) and 3 – \(\sqrt{3}\)
Their sum is 2 + \(\sqrt{3}\) + 3 – 3\(\sqrt{3}\) which is a rational number.
But the sum of 3 + \(\sqrt{5}\) and 4 – \(\sqrt{7}\) is not a rational number. So the sum of two irrational numbers is either rational or irrational.
(ii) Again taking two irrational numbers as π and \(\frac{3}{\pi}\) their product is \(\sqrt{3}\) and \(\sqrt{2}\) = \(\sqrt{3}\) × \(\sqrt{2}\) which is irrational, So the product of two irrational numbers is either rational or irrational.
Question 5.
Find a positive number smaller than \(\frac{1}{2^{1000}}\). Justify.
Solution:

There will not be a positive number smaller than 0.
So there will not be a +ve number smaller than \(\frac{1}{2^{1000}}\)
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.1 Additional Questions
Question 1.
Prove that \(\sqrt{5}\) is an irrational number.
Solution:
Suppose that \(\sqrt{5}\) is rational
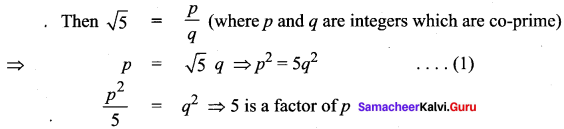
So let p = 5c
substitute p = 5c in (1) we get
(5c)2 = 5q2 ⇒ 25c2 = 5q2
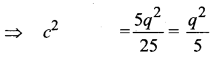
⇒ 5 is a factor of q also
So 5 is a factor of p and q which is a contradiction.
⇒ \(\sqrt{5}\) is not a rational number
⇒ \(\sqrt{5}\) is an irrational number
![]()
Question 2.
Prove that 0.33333 = \(\frac{1}{3}\)
Solution:
Let x = 0.33333….
10x = 3.3333 ….
10x – x = 9x = 3
![]()