Students can Download Maths Chapter 2 Measurements Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Additional Questions
Additional Questions And Answers
Exercise 2.1
Very Short Answers [2 Marks]
Question 1.
Find the length of arc if the perimeter of sector is 45 cm and radius is 10 cm.
Solution:
Given Radius of the sector = 10 cm
Perimeter of the sector P = 45 cm
l + 2r = 45
l + 2(10) = 45
l + 20 = 45
l = 45 – 20
l = 25 cm
Length of the arc l = 25 cm
Question 2.
Find the radius of sector whose perimeter and length of arc are 30 cm and 16 cm respectively.
Solution:
Given length of the arc = 16 cm
Perimeter of the arc = 30 cm
l + 2r = 30
16 + 2 r = 30
2 r = 30 – 16
2 r = 14
r = \(\frac{14}{2}\)
r = 7 cm
Radius of the sector = 7 cm
Question 3.
Find the length of arc whose radius is 7 cm and central angle 90°.
Solution:
Here θ = 90°; radius r = 7cm
Length of the arc = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
= \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 7 = 11 cm
∴ Length of the arc = 11 cm
![]()
Short Answers [3 Marks]
Question 1.
Find the length arc whose radius is 42 cm and central angle is 60°.
Solution:
Length of the arc = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
Given central angle 0 = 60°
Radius of the sector r = 42 cm
l = \(\frac{60^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 42 = 44 cm
∴ Length of the arc = 44 cm
Question 2.
Find the length of the arc whose radius is 10.5 cm and central angle is 36°.
Solution:

∴ Length of the arc = 6.6 cm
Long Answers [5 Marks]
Question 1.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of its arc and area of the sector.
Solution:
Radius of the sector = 21 cm
Length of the arc

∴ Length of the arc = 55 cm
Area of the sector = 577.5 cm2
Question 2.
Find the perimeter of sector whose area is 324 sq. cm and radius is 27 cm.
Solution:
Radius of the sector = 27 cm
Area of the sector =324 cm2

Perimeter of the sector P = (l + 2r) units = 24 + 2(27) cm = (24 + 54) cm = 78 cm
Exercise 2.2
Question 1.
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal semi-circles drawn on PQ and Question as diameters. Find the p perimeter and area of the shaded region.

Solution:
PS = Diameter of a circle of radius 6 cm = 12 cm
PQ = QR = RS = \(\frac{12}{3}\) = 4 cm Question = QR + RS = 4 + 4 = 8 cm
∴ Perimeter of the shaded part = Arc length of semi-circle of radius 6 cm + Arc length of semicircle of radius 4 cm + Arc length of semi-circle of radius 2 cm.
= (π × 6) + (π × 4) + (π × 2) cm
P = 12 π cm
Area required = Area of semicircle with PS as diameter + Area of semi circle with PQ as diameter – Area of semi-circle with Question as diameter.

Question 2.
In the figure AOBCA represents a quadrant of a circle of radius 3.5cm with center ‘O’ calculate the area of the shaded portion (π = \(\frac{22}{7}\))

Solution:

∴ Area of shaded region = Area of the quadrant – Area of triangle
= 9.625 – 3.5 cm2 = 6.125 cm2
Question 3.
Find the area of the shaded region in the figure
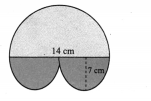
Solution:
Radius of the big semicircle = 14 cm

∴ Required area = 308 + 154 cm2 = 462 cm2
![]()
Exercise 2.3
Very Short Answers [2 Marks]
Question 1.
What is the least number of planes that can enclose a solid? What is the name of the solid?
Solution:
Least number of planes = 4, the solid is tetrahedron.
Question 2.
Can a polyhedron have for its faces = 12 edges = 16 and vertices = 6.
Solution:
Verifying Euler’s formula
F + V – E = 12 + 6 – 16 = 18 – 16 = 2
Yes, the polyhedron can have F = 12, E = 16 and V = 6
Short Answers [3 Marks]
Question 1.
Verify Euler’s formula for a pyramid.
Solution:
A pyramid has faces = 5, Vertices = 5, Edges = 8
By Euler’s formula F + V – E = 5 + 5 – 8 = 10 – 8 = 2
Question 2.
Verify Eulers formula for a triangular prism.
Solution:
For a triangular prism
Faces = 5, Edges = 9, Vertices = 6
By Euler’s formula F + V – E = 5 + 6 – 9 = 11 – 9 = 2
![]()
Long Answers [5 Marks]
Question 1.
(a) Dice are cubes where the numbers on the opposite faces must total 7. Is the following a die.
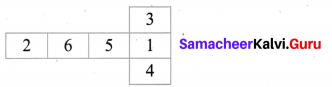
(b) The following shows a net with areas of faces. What can be the shape?

Solution:
(a) 2 + 5 = 6 + 1 = 3 + 4 = 7
∴ It can be a die.
(b) It is a cuboid