You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.5
Exercise 1.5 Class 10 Maths Samacheer Question 1
Using the functions f and g given below, find fog and gof. Check whether fog = gof.
(i) f(x) = x – 6, g(x) = x2
(ii) f(x) = \(\frac{2}{x}\), g(x) = 2x2 – 1
(iii) f(x) = \(\frac{x+6}{3}\) g(x) = 3 – x
(iv) f(x) = 3 + x, g(x) = x – 4
(v) f(x) = 4x2– 1,g(x) = 1 + x
Solution:
(i) f(x) = x – 6, g(x) = x2
fog(x) = f(g(x)) = f(x2) = x2 – 6 …………….. (1)
gof(x) = g(f(x)) = g(x – 6) = (x – 6)2
= x2 + 36 – 12x = x2 – 12x + 36 ……………… (2)
(1) ≠ (2)
∴ fog(x) ≠ gof(x)

(iii) f(x) = \(\frac{x+6}{3}\) g(x) = 3 – x
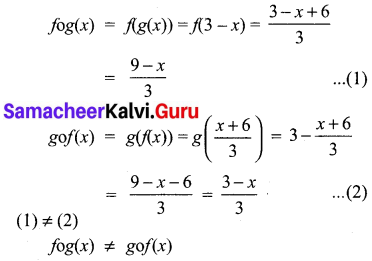
(iv) f(x) = 3 + x, g(x) = x – 4
fog(x) = f(g(x)) = f(x – 4) = 3 + x – 4
= x – 1 ………… (1)
gof(x) = g(f(x)) = g(3 + x) = 3 + x – 4
= x – 1 ……………… (2)
Here fog(x) = gof(x)
(v) f(x) = 4x2 – 1, g(x) = 1 + x
fog(x) = f(g(x)) = f(1 + x) = 4(1 + x)2 – 1
= 4(1 + x2 + 2x) – 1 = 4 + 4x2 + 8x – 1
= 4x2 + 8x + 3 ……………. (1)
gof(x) = g(f(x)) = g(4x2 – 1)
= 1 + 4x2 – 1 = 4x2 …………….. (2)
(1) ≠ (2)
∴ fog(x) ≠ gof(x)
10th Maths Exercise 1.5 Answers Question 2.
Find the value of k, such that f o g = g o f
(i) f(x) = 3x + 2, g(x) = 6x – k
Answer:
f(x) = 3x + 2 ;g(x) = 6x – k
fog = f[g(x)]
= f (6x – k)
= 3(6x – k) + 2
= 18x – 3K + 2
g0f= g [f(x)]
= g (3x + 2)
= 6(3x + 2) – k
= 18x + 12 – k
But given fog = gof.
18x – 3x + 2 = 18x + 12 – k
-3k + 2 = 12 – k
-3 k + k = 12-2
-2k = 10
k = \(\frac { -10 }{ 2 } \) = -5
The value of k = -5
(ii) f(x) = 2x – k, g(x) = 4x + 5
Answer:
f(x) = 2x – k ; g(x) = 4x + 5
fog = f[g(x)]
= f(4x + 5)
= 2(4x + 5) – k
= 8x + 10 – k
gof = g [f(x)]
= g(2x – k)
= 4(2x – k) + 5
= 8x – 4k + 5
But fog = gof
8x + 10 – k = 8x – 4k + 5
-k + 4k = 5 – 10
3k = -5
k = \(\frac { -5 }{ 3 } \)
The value of k = \(\frac { -5 }{ 3 } \)
10th Maths Exercise 1.5 Samacheer Kalvi Question 3.
if f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\), show that fog = gof = x
Solution:
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\), fog = gof = x

Ex 1.5 Class 10 Samacheer Question 4.
(i) If f (x) = x2 – 1, g(x) = x – 2 find a, if g o f(a) = 1.
(a) Find k, if f(k) = 2k -1 and
fof (k) = 5.
Answer:
(i) f(x) = x2 – 1 ; g(x) = x – 2 .
gof = g [f(x)]
= g(x2 – 1)
= x2 – 1 – 2
= x2 – 3
given gof (a) = 1
a2 – 3 = 1 [But go f(x) = x2 – 3]
a2 = 4
a = \(\sqrt { 4 }\) = ± 2
The value of a = ± 2
(ii) f(k) = 2k – 1 ; fof(k) = 5
fof = f[f(k)]
= f(2k – 1)
= 2(2k – 1) – 1
= 4k – 2 – 1
= 4k – 3
fof (k) = 5
4k – 3 = 5
4k = 5 + 3
4k = 8
k = \(\frac { 8 }{ 4 } \) = 2
The value of k = 2
10th Maths | Exercise 1.5 Answers Question 5.
Let A,B,C ⊂ N and a function f: A → B be defined by f(x) = 2x + 1 and g : B → C be defined by g(x) = x2. Find the range of fog and gof
Solution:
f(x) = 2x + 1
g(x) = x2
fog(x) = fg(x)) = f(x2) = 2x2 + 1
gof(x) = g(f(x)) = g(2x + 1) = (2x + 1)2
= 4x2 + 4x + 1
Range of fog is
{y/y = 2x2 + 1, x ∈ N}
Range of gof is
{y/y = (2x + 1)2, x ∈ N}.
10th Maths 1.5 Exercise Question 6.
Let f(x) = x2 – 1. Find (i) fof (ii) fofof
Answer:
f(x) = x2 – 1
(i) fof = f[f{x)]
= f(x2 – 1)
= (x2 – 1)2 – 1
= x4 – 2x2 + 1 – 1
= x4 – 2x2
(ii) fofof = fof[f(x)]
= fof (x2 – 1)
= f(x2 – 1)2 – 1
= f(x4 – 2x2 + 1 – 1)
= f (x4 – 2x2)
fofof = (x4 – 2x2)2 – 1
10th Maths Exercise 1.5 Question 7.
If f: R → R and g : R → R are defined by f(x) = x5 and g(x) = x4 then check if f,g are one-one and fog is one-one?
Solution:
f(x) = x5
g(x) = x4
fog = fog(x) = f(g(x)) = f(x4)
= (x4)5 = x20
f is one-one, g is not one-one.
∵ g(1) = 14 = 1
g(-1) = ( -1)4 = 1
Different elements have same images
fog is not one-one. [∵ fog (1) = fog (-1) = 1]
Samacheer Kalvi 10th Maths Exercise 1.5 Question 8.
Consider the functions f(x), g(x), h(x) as given below. Show that
(f o g) o h = f o(g o h) in each case.
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x2
(ii) f(x) = x2, g(x) = 2x and h(x) = x + 4
(iii) f(x) = x – 4, g(x) = x2 and h(x) = 3x – 5
Answer:
(i) f(x) = x – 1, g (x) = 3x + 1, h(x) = x2
fog (x) = f[g(x)]
= f(3x + 1)
= 3x + 1 – 1
fog = 3x
(fog) o h(x) = fog [h(x)] ,
= fog (x2)
= 3(x2)
(fog) oh = 3x2 …..(1)
goh (x) = g[h(x)]
= g(x2)
= 3(x2) + 1
= 3x2 +1
fo(goh) x = f [goh(x)]
= f[3x2 + 1]
= 3x2 + 1 – 1
= 3x2 ….(2)
From (1) and (2) we get
(fog) oh = fo (goh)
Hence it is verified
(ii) f(x) = x2 ; g (x) = 2x and h(x) = x + 4
(fog) x = f[g(x)]
= f (2x)
= (2x)2
= 4x2
(fog) oh (x) = fog [h(x)]
= fog (x + 4)
= 4(x + 4)2
= 4[x2 + 8x + 16]
= 4x2 + 32x + 64 …. (1)
goh (x) = g[h(x)]
= g(x + 4)
= 2(x + 4)
= 2x + 8
fo(goh) x = fo [goh(x)]
= f[2x + 8]
= (2x + 8)2
= 4×2 + 32x + 64 …. (2)
From (1) and (2) we get
(fog) oh = fo(goh)
(iii) f(x) = x – 4 ; g (x) = x2; h(x) = 3x – 5
fog (x) = f[g(x)]
= f(x2)
= x2 – 4
(fog) oh (x) = fog [h(x)]
= fog (3x – 5)
= (3x – 5)2 – 4
= 9x2 – 30x + 25 – 4
= 9x2 – 30x + 21 ….(1)
goh (x) = g[h(x)]
= g(3x – 5)
= (3x – 5)2
= 9x2 + 25 – 30x
fo(goh)x = f[goh(x)]
= f[9x2 – 30x + 25]
= 9x2 – 30x + 25 – 4
= 9x2 – 30x + 21 ….(2)
From (1) and (2) we get
(fog) oh = fo(goh)
Exercise 1.5 Class 10 Maths Question 9.
Let f ={(-1, 3),(0, -1),(2, -9)} be a linear function from Z into Z . Find f(x).
Solution:
f ={(-1, 3), (0, -1), 2, -9)
f(x) = (ax) + b ………… (1)
is the equation of all linear functions.
∴ f(-1) = 3
f(0) = -1
f(2) = -9
f(x) = ax + b
f(-1) = -a + b = 3 …………… (2)
f(0) = b = -1
-a – 1 = 3 [∵ substituting b = – 1 in (2)]
-a = 4
a = -4
The linear function is -4x – 1. [From (1)]
10th Maths 1.5 Exercise Question 10.
In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at1 + bt2) = aC(t1) + bC(t2), where a, b are constants. Show that the circuit C(t) = 31 is linear.
Answer:
Given C(t) = 3t
C(at1) = 3at1 …. (1)
C(bt2) = 3 bt2 …. (2)
Add (1) and (2)
C(at1) + C(bt2) = 3at1 + 3bt2
C(at1 + bt2) = 3at1 + 3bt2
= Cat1 + Cbt2 [from (1) and (2)]
∴ C(at1 + bt2) = C(at1 + bt2)
Superposition principle is satisfied.
∴ C(t) = 3t is a linear function.