You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.12
10th Maths Exercise 3.12 Samacheer Kalvi Question 1.
If the difference between a number and its reciprocal is \(\frac{24}{5}\), find the number.
Solution:
Let a number be x.
Its reciprocal is \(\frac{1}{x}\)
\(x-\frac{1}{x}=\frac{24}{5}\)
\(\frac{x^{2}-1}{x}=\frac{24}{5}\)
5x2 – 5 -24x = 0 ⇒ 5x2 – 24x – 5 = 0
5x2 – 25x + x – 5 = 0
5x(x – 5) + 1 (x – 5) = 0
(5x + 1)(x – 5) = 0
x = \(\frac{-1}{5}\), 5
∴ The number is \(\frac{-1}{5}\) or 5.
10th Maths Exercise 3.12 Solution Question 2.
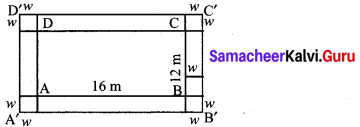
A garden measuring 12m by 16m is to have a pedestrian pathway that is ‘w’ meters wide installed all the way around so that it increases the total area to 285 m2. What is the width of the pathway?
Solution:
Area of ABCD = 16 × 12 2
= 192 m2
Area of A’B’C’D’ (12 + 2w)(16 + 2w)
192 + 32 w + 24 w + 4 w2 = 285
4w2 + 56w – 93 = 0
4w2 + 62w – 6w – 93 = 0
2w(2w + 31) – 3(2w + 31) = 0
(2w – 3)(2w + 31) = 0
w = 1.5 or \(\frac{-31}{2}\) = 15.5
w = – 15.5 cannot possible 3
∴ w = \(\frac{3}{2}\) = 1.5 m
(w cannot be (-ve))
The width of the pathway = 1.5 m.
Ex 3.12 Class 10 Samacheer Question 3.
A bus covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hour more it would have taken 30 minutes less for the journey. Find the original speed of the bus.
Solution:
Let x km/hr be the constant speed of the bus.
The time taken to cover 90 km = \(\frac{90}{x}\) hrs.
When the speed is increased bus 15 km/hr.
= \(\frac{90}{x+15}\)
It is given that the time to cover 90 km is reduced by \(\frac{1}{2}\) hrs.

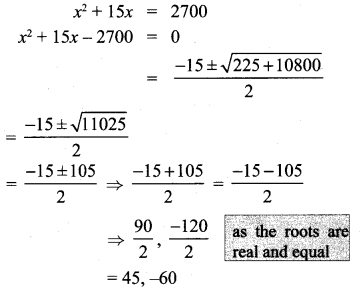
The speed of the bus cannot be -ve value.
∴ The original speed of the bus is 45 km/hr.
Exercise 3.12 Class 10 Samacheer Question 4.
A girl is twice as old as her sister. Five years hence, the product of their ages (in years) will be 375. Find their present ages.
Solution:
Let the age of the girl be = 2y years
Her sister’s age is = y years
(2y + 5)(y + 5) = 375
2y2 + 5y+ 10y + 25 – 375 = 0
2y2 + 15y – 350 = 0

y = 10, y cannot be (-ve).
∴ Girls age is 2y = 20 years.
Her sister’s age = y = 10 years.
10th Maths Exercise 3.12 Question 5.
A pole has to be erected at a point on the T boundary of a circular ground of diameter j 20 m in such a way that the difference of its i distances from two diametrically opposite j fixed gates P and Q on the boundary is 4 m. Is i it possible to do so? If answer is yes at what j distance from the two gates should the pole j be erected?
Solution:
PQ = 20 m
PX – XQ = 4 m …………… (1)
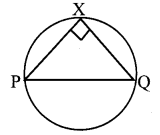
Squaring both sides,
PX2 + XQ2 – 2PX . QX = 16 (∵ ∠Q × p = 90°)
PQ2 – 2P × QX = 16
400 – 16 = 2PX × QX
384 = 2PX – QX
PX . QX = 192
∴ (PX + QX)2 = PX2 + QX2 + 2PX . QX
= 400 + 2 × 192
= 784 = 282
∴ PX + QX = 28
From (1) & (2) 2PX = 32 ⇒ PX = 16 m QX = 12 m
∴Yes, the distance from the two gates to the pole PX and QX is 12 m, 16m.
Samacheer Kalvi Guru 10th Maths Question 6.
From a group of black bees 2x2, square root of half of the group went to a tree. Again eight- ninth of the bees went to the same tree. The remaining two got caught up in a fragrant lotus. How many bees were there in total?
Solution:
Total no. of bees = 2x2

18x2 – 9x – 16x2 = 2 × 9
2x2 – 9x – 18 = 0
(x – 6)(2x + 3) = 0
x = 6, x = \(\frac{-3}{2}\) (it is not possible)
No. of bees in total = 2x2
= 2 × 62 = 72
10th Maths Algebra Exercise 3.12 Question 7.
Music is been played in two opposite galleries with certain group of people. In the first gallery a group of 4 singers were singing and in the second gallery 9 singers were singing. The two galleries are separated by the distance of 70 m. Where should a person stand for hearing the same intensity of the singers voice? (Hint: The ratio of the sound intensity is equal to the square of the ratio of their corresponding distances).
Solution:
Let the person stand at a distance ‘d’ from 2nd gallery having 9 singers.
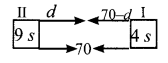
Given that ratio of sound intensity is equal to the square of the ratio of their corresponding distance.
∴ \(\frac{9}{4}=\frac{d^{2}}{(70-d)^{2}}\)
4d2 = 9(70 – d)2
4d2 = 9(702 – 140d + d2)
4d2 = 9 × 702 – 9 × 140d + 9d2
∴ 5d2 – 9 × 140d + 9 × 702 = 0
5d2 = 1260d + 44100 = 0
d2 – 252d + 8820 = 0

= \(\frac{420}{2} \text { or } \frac{84}{2}\)
= 120 or 42
∴ The person stand at a distance 28m from the first and 42 m from second gallery.
Samacheer Kalvi.Guru 10th Maths Question 8.
There is a square field whose side is 10 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at ₹ 3 and ₹ 4 per square metre respectively is ₹364. Find the width of the gravel path.
Solution:
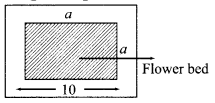
Area of the flower bed = a2
Area of the gravel path = 100 – a2
Area of total garden =100
given cost of flower bed + gravelling = ₹ 364
3a2 + 4 (100 – a2) = ₹ 364
3a2 + 400 – 4a2 = 364
∴ a2 = 400 – 364
= 36 ⇒ a = 6
width of gravel path =\(\frac{10-6}{2}=\frac{4}{2}\) = 2 cm
10th Maths Exercise 3.12 9th Sum Question 9.
Two women together took 100 eggs to a market, one had more than the other. Both sold them for the same sum of money. The first then said to the second: “If I had your eggs, I would have earned ₹ 15”, to which the second replied: “If I had your eggs, I would have earned ₹ 6 \(\frac { 2 }{ 3 } \)”. How many eggs did each had in the beginning? Answer:
Number of eggs for the first women be ‘x’
Let the selling price of each women be ‘y’
Selling price of one egg for the first women = \(\frac { y }{ 100-x } \)
By the given condition
(100 – x) \(\frac { y }{ x } \) = 15 (for first women)
y = \(\frac { 15 }{ 100-x } \) ……(1)
x × \(\frac { y }{ (100-x) } \) = \(\frac { 20 }{ 3 } \) [For second women]
y = \(\frac { 20(100-x) }{ 3x } \) ……..(2)
From (1) and (2) We get
\(\frac { 15 }{ 100-x } \) = \(\frac { 20(100-x) }{ 3x } \)
45x2 = 20(100 – x)2
(100 – x)2 = \(\frac{45 x^{2}}{20}\) = \(\frac { 9 }{ 4 } \) x2
∴ 100 – x = \(\sqrt{\frac{9}{4} x^{2}}\)
100 – x = \(\frac { 3x }{ 2 } \)
3x = 2(100 – x)
3x = 200 – 2x
3x + 2x = 200 ⇒ 5x = 200
x = \(\frac { 200 }{ 5 } \) ⇒ x = 40
Number of eggs with the first women = 40
Number of eggs with the second women = (100 – 40) = 60
10th Maths Exercise 3.12 In Tamil Question 10.
The hypotenuse of a right-angled triangle is 25 cm and its perimeter 56 cm. Find the length of the smallest side.
Solution:
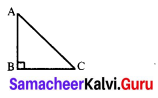
AB + BC + CA = 56 cm
AC = 25 cm
AB + BC = 56 – 25 = 31
AB2 + BC2 = AC2
(AB + BC)2 – 2AB . BC = AC2 [∵ a2 + b2 = (a + b)2 – 2ab]
312 – 2AB . BC = 252
-2AB . BC = 625 – 961

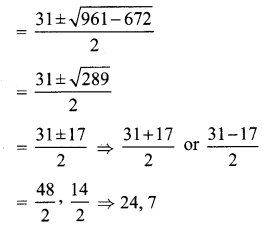
∴ The length of the smallest side is 7 cm.