Samacheer Kalvi 11th Maths Guide Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 10 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 10.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.2

பின்வரும் சார்புகளைத் தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக.

Question 1.
f(x) = x – 3 sinx
தீர்வு :
f(x) = x – 3 sinx
f'(x) = \(\frac{d}{d x}\)(x) – 3\(\frac{d}{d x}\)(sin x)
= 1 – 3 cos x.

Question 2.
y = sin x + cos x
தீர்வு :
y = sin x + cos x
\(\frac{d y}{d \theta}\) = \(\frac{d}{d x}\) (sin x) + \(\frac{d}{d x}\) (cos x)
= cos x – sinx.

Question 3.
f(x) = x sin x
தீர்வு :
f(x) = x sin x
f'(x) = x . \(\frac{d}{d x}\) (sin x) + sin x . \(\frac{d}{d x}\) (x)
= x. cos x + sin x (1)
= x. cos x + sin x

Question 4.
y = cos x- 2 tan x
தீர்வு :
y = cos x – 2 tan x
\(\frac{d y}{d \theta}\) = \(\frac{d}{d x}\)(cos x) – 2 . \(\frac{d}{d x}\)(tan x)
= – sinx – 2 sec² x.

Question 5.
g(t) = t³ cost
தீர்வு :
g(t) = t³ cost
g'(t) = t³ \(\frac{d}{d t}\) (cos t) + cos t \(\frac{d}{d t}\) (t³)
(பெருக்கல் விதிப்படி)
= t³ (- sint) + cos t (3t²)
= 3t² cost – t³ sin t

Question 6.
g(t) = 4 sec t + tan t.
தீர்வு :
g(t) = 4 sec t + tan t
g'(t) = 4 . \(\frac{d}{d t}\)(sec t) + \(\frac{d}{d t}\)(tan t)
= 4 sec t tan t + sec² t

Question 7.
y = e^x sinx
தீர்வு :
y = e^x sinx
பெருக்கல் விதியைப் பயன்படுத்தி
\(\frac{d y}{d \theta}\) = e^x. \(\frac{d}{d x}\)(sin x) + sin x . \(\frac{d}{d x}\) (e^x)
= e^x . cos x + sin x . e^x = e^x (cos x + sin x)

Question 8.
y = \(\frac{\tan x}{x}\)
தீர்வு :
y = \(\frac{\tan x}{x}\)
வகுத்தல் விதியைப் பயன்படுத்தி
\(\frac{d y}{d \theta}\) = \(\frac{x \cdot \frac{d}{d x}(\tan x)-\tan x \cdot \frac{d}{d x}(x)}{x^{2}}\)
= \(\frac{x \cdot \sec ^{2} x-\tan x(1)}{x^{2}}\)
= \(\frac{x \sec ^{2} x-\tan x}{x^{2}}\)

Question 9.
y = \(\frac{\sin x}{1+\cos x}\)
வகுத்தல் விதியைப் பயன்படுத்தி

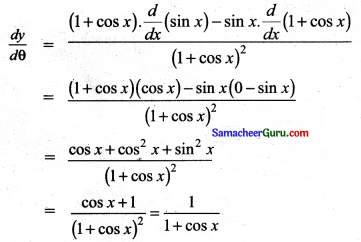
Question 10.
y = \(\frac{x}{\sin x+\cos x}\)
தீர்வு :
y = \(\frac{x}{\sin x+\cos x}\)
வகுத்தல் விதிப்படி

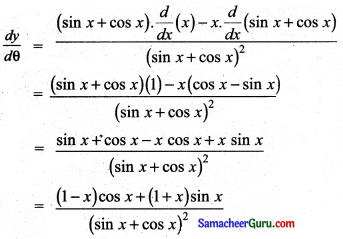
Question 11.
y = \(\frac{\tan x-1}{\sec x}\)
தீர்வு :

Question 12.
y = \(\frac{\sin x}{x^{2}}\)
தீர்வு :
y = \(\frac{\sin x}{x^{2}}\)
வகுத்தல் விதிப்படி,
\(\frac{d y}{d \theta}\) = \(\frac{x^{2} \cdot \frac{d}{d x}(\sin x)-\sin x \cdot \frac{d}{d x}\left(x^{2}\right)}{x^{4}}\)

= \(\frac{x^{2} \cos x-\sin x(2 x)}{x^{4}}\)

= \(\frac{x[x \cos x-2 \sin x]}{x^{4}}\)

= \(\frac{x \cos x-2 \sin x}{x^{3}}\)

Question 13.
y = tan θ (sin θ + cos θ)
தீர்வு :
y = tan θ (sin θ + cos θ)
\(\frac{d y}{d \theta}\) = tan θ . \(\frac{d}{d \theta}\)(sin θ + cos θ) + (sin θ + cos θ). \(\frac{d}{d \theta}\)(tan θ).
= tan (cos θ – sin θ) + (sin θ + cos θ) sec² θ
= \(\frac{\sin \theta}{\cos \theta}\) (cos θ – sin θ) + \(\frac{1}{\cos ^{2} \theta}\) (sin θ + cos θ)
= sin θ + \(\frac{\sin ^{2} \theta}{\cos \theta}+\frac{\sin \theta}{\cos ^{2} \theta}+\frac{\cos \theta}{\cos ^{2} \theta}\)

= sin θ – \(\frac{\sin ^{2} \theta}{\cos \theta}+\frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\cos \theta}+\frac{1}{\cos \theta}\)

= sin θ + \(\frac{1-\sin ^{2} \theta}{\cos \theta}\) + tan θ . sec θ

= sin θ + \(\frac{\cos ^{2} \theta}{\cos \theta}\) + tan θ . sec θ
\(\frac{d y}{d \theta}\) = sin θ + cos θ + tan θ sec θ.

Question 14.
y = cosec x – cot x
தீர்வு :
y = cosec x . cot x
\(\frac{d y}{d \theta}\) = cosec x. \(\frac{d}{d x}\)(cot x) + cot x. \(\frac{d}{d x}\) (cosec x)
= cosec x (- cosec² x) + cot x(-cosec x cot x)
= -cosec³ x – cot² x cosec x
= \(-\frac{1}{\sin ^{3} x}-\frac{\cos ^{2} x}{\sin ^{2} x} \cdot \frac{1}{\sin x}\)
= –\(\left[\frac{1}{\sin ^{3} x}+\frac{\cos ^{2} x}{\sin ^{3} x}\right]\)
\(\frac{d y}{d \theta}\) = – \(\left[\frac{1+\cos ^{2} x}{\sin ^{3} x}\right]\)

Question 15.
y = x sin x cos x
தீர்வு :
y = x sin x cos x in = x sin x. (cos x)+ x. *(sivo x)
\(\frac{d y}{d \theta}\) = x sin x . \(\frac{d}{d x}\) (cos x) + x . \(\frac{d}{d x}\) (sin x) . cos x + \(\frac{d}{d x}\) (x) . sin x . cos x [வகுத்தல் விதிப்படி]
= x sin x (-sin x) + x cos x.cos x + 1 . sin x cos x
= – x sin² x + x cos² x + sin x cos x
= x (cos² x – sin² x) + sin x cos x
\(\frac{d y}{d \theta}\) = x cos 2x + sin x cosx [∵ cos² x – sin² x = cos 2x]

Question 16.
y = e^-x log x
தீர்வு :
y = e^-x log x
\(\frac{d y}{d \theta}\) = e^-x . \(\frac{d}{d x}\)(log x) + x . \(\frac{d}{d x}\)(e^-x)

= e^-x . \(\frac{1}{x}\) + log x e^-x(-1)
= \(\frac{e^{-x}}{x}\) – e^-x log x
\(\frac{d y}{d \theta}\) = \(\frac{d y}{d \theta}\)(\(\frac{1}{x}\) – log x)

Question 17.
y = (x² + 5) . ln(1 + x)e^-3x
தீர்வு :
y = (x² + 5) . log(1 + x)e^-3x)
\(\frac{d y}{d \theta}\) = (x² + 5) . log(1 + x) . \(\frac{d}{d x}\)(e^-3x) + (x² + 5) . \(\frac{d}{d x}\)log(1 + x)e^-3x + \(\frac{d}{d x}\) (x² + 5) . log(1 + x) e^-3x
= (x² + 5) . log(1 + x)e^-3x(-3) + (x² + 5) . \(\frac{1}{1+x}\) . e^-3x + 2x . log(1 + x)e^-3x
= e^-3x[-3(x² + 5)log(1 + x) + \(\frac{x^{2}+5}{1+x}\) + 2x log(1 + x)]

Question 18.
y = sin x⁰
தீர்வு :
y = sin x⁰
x⁰ = x × \(\frac{pi}{180}\) ஆரையன் = \(\frac{pi x}{180}\)
∴ y = sin \(\frac{pi}{180}\) x
\(\frac{d y}{d \theta}\) = \(\frac{pi}{180}\) cos \(\frac{pi x}{180}\)

Question 19.
y = log₁₀ x
தீர்வு :
y = log₁₀ x
\(\frac{d y}{d \theta}\) = \(\frac{d}{d x}\)(log₁₀ × e log x)
= log₁₀ e . \(\frac{1}{x}\) = \(\frac{\log _{10} e}{x}\)

Question 20.
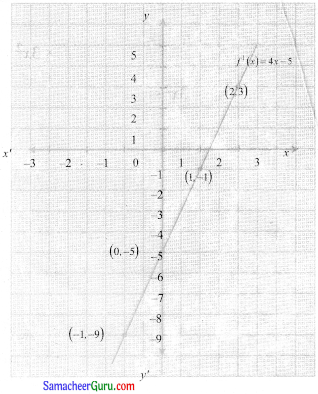
f(x) = 2x² – 5x + 3 எனில் f ‘(x) என்ற சார்பின் வரைபடம் வரைக.
தீர்வு :
f(x) = 2x² – 5x + 3
f'(x) = 2 . \(\frac{d}{d x}\)(x²) – 5 . \(\frac{d}{d x}\)(x) + \(\frac{d}{d x}\)(3)
= 2(2x) – 5(1) + 0
f'(x) = 4x – 5