Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 12 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 12.5 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 12 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 12.5
சரியான அல்லது மிகவும் ஏற்புடைய விடையினை கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
Question 1.
மூன்று ஆண்கள், இரு பெண்கள் மற்றும் நான்கு குழந்தைகள் உள்ள ஒரு குழுவிலிருந்து சமவாய்ப்பு முறையில் நான்கு நபர்கள் தேர்ந்தெடுக்கப் படுகின்றனர். அவர்களில் சரியாக இருவர் மட்டும் குழந்தைகளாக இருப்பதற்கான நிகழ்தகவு.
(1) \(\frac{3}{4}\)
(2) \(\frac{10}{25}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{10}{21}\)
குறிப்பு :
நான்கு நபர்கள் 9 பேர்களிலிருந்து தேர்வு செய்வது = \({ }^{9} \mathrm{C}_{4}\) = 126
சரியாக 2 குழந்தைகள் இருக்கும் 4 பேர் கொண்ட குழு தேர்வு செய்வது = \({ }^{4} \mathrm{C}_{2}\) × \({ }^{5} \mathrm{C}_{2}\) = 60
∴ தேவையான நிகழ்தகவு = \(\frac{60}{126}\) = \(\frac{10}{21}\)
விடை :
(4)
Question 2.
{1, 2, 3,….., 20} என்ற கணத்திலிருந்து ஒரு எண் தேர்ந்தெடுக்கப்படுகிறது. அந்த எண் 3 அல்லது 4 ஆல் வகுபடுவதற்கான நிகழ்தகவு.
(1) \(\frac{2}{5}\)
(2) \(\frac{1}{8}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{2}{3}\)
குறிப்பு :
S = {1, 2, 3,… 20} ⇒ n(s) = 20 A = 3-ல் வகுபடும் எண்
= {3,6,9,12, 15, 18} ⇒ n(A) = 6 B = 4 -ல் வகுபடும் எண்
= {4, 8, 12, 16, 20} ⇒n(B) = 5
A∩B = {12}
⇒ n (A∩B) = 1
∴ P(A U B) = P(A) + P(B) – P(A∩B)
= \(\frac{6}{20}+\frac{5}{20}-\frac{1}{20}\)
= \(\frac{6+5-1}{20}\)
= \(\frac{10}{20}\)
= \(\frac{1}{2}\)
விடை :
(3) \(\frac{1}{2}\)
Question 3.
A, B , மற்றும் C தனித்தனியாக ஒரே சமயத்தில் ஒரு இலக்கை நோக்கிச் சுடுகின்றனர். அவர்கள் அந்த இலக்கைச் சுடுவதற்கான நிகழ்தகவுகள் முறையே \(\frac{3}{4}\), \(\frac{1}{2}\), \(\frac{5}{8}\) எனில் A அல்லது B அந்த இலக்கைச்சரியாகச் சுடவும் ஆனால் அந்த இலக்கை C சரியாகச் சுடாமல் இருப்பதற்கான நிகழ்தகவானது
(1) \(\frac{21}{64}\)
(2) \(\frac{7}{32}\)
(3) \(\frac{9}{64}\)
(4) \(\frac{7}{8}\)
குறிப்பு:
P(A) = \(\frac{3}{4}\) , P(B) = \(\frac{1}{2}\) , P(C) = \(\frac{5}{8}\)
P(\(\overline{\mathrm{C}}\)) = 1 – \(\frac{5}{8}\) = \(\frac{3}{8}\)
∴ P(C) = 1 – P(A, Bயுடன் C இல்லாமல் இருப்பது)
= P(A∪ B∩\(\overline{\mathrm{C}}\)) = P(A∪B). P(\(\overline{\mathrm{C}}\))
= [P(A) + P(B) – P (A∩B]] P(\(\overline{\mathrm{C}}\))
= \(\left[\frac{3}{4}+\frac{1}{2}-\frac{3}{4} \cdot \frac{1}{2}\right]\left(\frac{3}{8}\right)\) – \(\left(\frac{3}{4}+\frac{1}{2}-\frac{3}{8}\right) \frac{3}{8}\)
= \(\left(\frac{6+4-3}{8}\right) \frac{3}{8}\)
= (\(\frac{7}{8}\)) (\(\frac{3}{8}\)) = \(\frac{21}{64}\)
விடை :
(1) \(\frac{21}{64}\)
![]()
Question 4.
A மற்றும் B என்பன இரு நிகழ்ச்சிகள் எனில் சரியாக ஒரு நிகழ்ச்சி நடப்பதற்கான நிகழ்தகவானது
(1) P(A∪\(\overline{\mathrm{B}}\)) + P(\(\overline{\mathrm{A}}\)∪B)
(2) P(A∩\(\overline{\mathrm{B}}\)) + P(\(\overline{\mathrm{A}}\)∩B)
(3) P(A) + P(B) – P(A∩B)
(4) P(A) + P(B) + 2P(A∩B)
குறிப்பு :
P (சரியாக ஒரு நிகழ்ச்சி நடப்பதற்கான நிகழ்தகவு) = P(AMB)+P(AMB)
விடை :
(2) P(A∩\(\overline{\mathrm{B}}\)) + P(\(\overline{\mathrm{A}}\)∩B)
Question 5.
A மற்றும் B இரு நிகழ்ச்சிகளுக்கு P(\(\overline{\mathbf{A} \cup \mathbf{B}}\)) = \(\frac{1}{6}\), P(A∩B) = \(\frac{1}{4}\) மற்றும் P(\(\overline{\mathrm{A}}\)) = \(\frac{1}{4}\) எனில் நிகழ்ச்சிகள் A-யும் B -யும்
(1) சமவாய்ப்பு நிகழ்ச்சிகள் ஆனால் சார்பிலா நிகழ்ச்சிகள் அல்ல
(2) சார்பிலா நிகழ்ச்சிகள் ஆனால் சமவாய்ப்பு நிகழ்ச்சிகள் அல்ல
(3) சார்பிலா நிகழ்ச்சிகள் மற்றும் சமவாய்ப்பு நிகழ்ச்சிகள்
(4) ஒன்றையொன்று விலக்கா நிகழ்ச்சிகள் மற்றும் சார்புள்ள நிகழ்ச்சிகள்
குறிப்பு :
P (\(\overline{\mathbf{A} \cup \mathbf{B}}\)) = \(\frac{1}{6}\)
P (A∩B) = \(\frac{1}{4}\), P(\(\overline{\mathrm{A}}\)) = \(\frac{1}{4}\)
P (\(\overline{\mathbf{A} \cup \mathbf{B}}\)) = 1 – P(A∪B)
\(\frac{1}{6}\) = 1 – P(A∪B)
⇒ P(A∪B) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
P(\(\overline{\mathrm{A}}\)) = \(\frac{1}{4}\)
⇒ P(A) =1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
P(A∪B) = P(A) + P(B) – P(A∩B)
\(\frac{5}{6}\) = \(\frac{3}{4}\) + P(B) – \(\frac{1}{4}\)
⇒ P(B) = \(\frac{5}{6}\) – \(\frac{3}{4}\) + \(\frac{1}{4}\)
∴ P(B) = \(\frac{5}{6}\) – \(\frac{1}{2}\)
= \(\frac{5-3}{6}\)
= \(\frac{2}{6}\) = \(\frac{1}{3}\)
P(A∩B) = P(A) . P(B)
\(\frac{1}{4}\) = \(\frac{3}{4}\) \(\frac{1}{2}\) = \(\frac{1}{2}\)
∴ A , B சார்பிலா நிகழ்ச்சிகள் மற்றும் P(A) ≠ P(B)
விடை :
(2) சார்பிலா நிகழ்ச்சிகள் ஆனால் சமவாய்ப்பு
Question 6.
நிகழ்ச்சிகள் அல்ல) நான்கு குறைபாடுள்ள பொருள்களைக் கொண்ட மொத்தம் 12பொருள்களிலிருந்து இருபொருள்களைத் தேர்ந்தெடுக்கும் போது அதில் குறைந்தது ஒரு பொருள் குறைபாடு உடையதாக இருப்பதற்கான நிகழ்தகவானது
(1) \(\frac{19}{33}\)
(2) \(\frac{17}{33}\)
(3) \(\frac{23}{33}\)
(4) \(\frac{13}{33}\)
குறிப்பு :
A- குறைபாடுடையதை தேர்ந்தெடுக்கும் நிகழ்வு
8 நல்ல பொருட்கள் 4 குறைபாடுடைய பொருட்கள்
∴ n(A) = \({ }^{8} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{1}+{ }^{8} \mathrm{C}_{0} \times{ }^{4} \mathrm{C}_{2}\)
= 8 × 4 + 1 × \(\frac{4 \times 3}{2 \times 1}\) = 32 + 6 = 38
n(S) = \({ }^{12} \mathrm{C}_{2}\) = 281
n(S) = \({ }^{12} \mathrm{C}_{2}=\frac{12 \times 11}{{2} \times 1}\) = 66
∴ P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{38}{66}=\frac{19}{33}\)
விடை :
(1) \(\frac{19}{33}\)
![]()
Question 7.
ஒரு நபரின் கைப்பையில் 3 ஐம்பது ரூபாய் நோட்டுகளும், : 4 நூறு ரூபாய் நோட்டுகளும் மற்றும் 6 ஐநூறு ரூபாய் நோட்டுகளும் உள்ளன. அவற்றிலிருந்து எடுக்கப்படும். இரு நோட்டுகளும் நூறு ரூபாய் நோட்டுகளாகக் கிடைப்பதற்கான நிகழ்தகவின் சாதக விகிதமானது?
(1) 1 : 12
(2) 12 : 1
(3) 13 : 1
(4) 1 : 13
குறிப்பு :
S கூறுவெளி, A-2 நூறு ரூபாய் எடுக்கும் நிகழ்வு.
∴ n(S) = \({ }^{13} \mathrm{C}_{2}=\frac{13 \times 12}{{2} \times 1}\)
n(A) = \({ }^{4} \mathrm{C}_{2}\) = \(\frac{4 \times 3}{2 \times 1}\) = 6
∴ n(A) = 78 – 6 = 72
சாதகவிகிதமானது 6 : 72 = 1 : 12
விடை :
(1) 1 : 12
Question 8.
ASSISTANT’ என்ற சொல்லிலிருந்து சமவாய்ப்பு முறையில் ஒரு எழுத்தும் ‘STATISTICS’ என்ற சொல்லிலிருந்து சமவாய்ப்பில் ஒரு எழுத்தும் தேர்ந்தெடுக்கப்படும் பொழுது அவ்விரு எழுத்துக்களும் ஒரே எழுத்தாக இருப்பதற்கான நிகழ்தகவானது.
(1) \(\frac{7}{45}\)
(2) \(\frac{17}{90}\)
(3) \(\frac{29}{90}\)
(4) \(\frac{19}{90}\)
குறிப்பு :
∴ n(S) = 9 × 10 = 90
A – ஒரே எழுத்து இருவார்த்தைகளிலிருந்தும் தேர்வு செய்தல்.
n(A) = n(S) + n (A) + n (T) + n(I)
= \({ }^{3} \mathrm{C}_{1} \times{ }^{3} \mathrm{C}_{1}+{ }^{2} \mathrm{C}_{1} \times{ }^{1} \mathrm{C}_{1}+{ }^{2} \mathrm{C}_{1} \times{ }^{3} \mathrm{C}_{1}+{ }^{1} \mathrm{C}_{1} \times{ }^{2} \mathrm{C}_{1}\)
= 3 × 3 + 2 × 1 + 2 × 3 + 1 × 2
= 9 + 2 + 6 + 2 = 19
∴ n (A) = 19
P(A) = \(\frac{19}{90}\)
விடை :
(4) \(\frac{19}{90}\)
Question 9.
வரிசை 2 உடைய அணிகள் கணத்தில் அணியின் உறுப்புகள் 0 அல்லது 1 மட்டுமே உள்ளது எனில் தேர்ந்தெடுக்கப்படும் அணியின் அணிக்கோவை மதிப்பு பூச்சியமற்றதாகக் கிடைப்பதற்கான நிகழ்தகவு.
(1) \(\frac{3}{16}\)
(2) \(\frac{3}{8}\)
(3) \(\frac{1}{4}\)
(4) \(\frac{5}{8}\)
குறிப்பு :
2 × 2 அணியில் அணிக்கோவை ) அல்லாத 0, 1 உறுப்புகளாகக் கொண்ட அணி
A = \(\left\{\left(\begin{array}{ll}
0 & 1 \\
1 & 1
\end{array}\right),\left(\begin{array}{ll}
1 & 0 \\
1 & 1
\end{array}\right)\left(\begin{array}{ll}
1 & 1 \\
0 & 1
\end{array}\right)\left(\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\right\}\)
∴ n (A) = 6
மொத்த எண்ணிக்கை n (S) = 24 = 16
∴ P(A) = \(\frac{6}{16}\) = \(\frac{3}{8}\)
விடை :
(2) \(\frac{3}{8}\)
![]()
Question 10.
ஒரு பையில் 5வெள்ளை மற்றும் 3 கருப்பு நிறப்பந்துகள் உள்ளன. பையிலிருந்து தொடர்ச்சியாக 5 பந்துகளை மீண்டும் வைக்கப்படாமல் எடுக்கும் போது பந்துக்களில் நிறம் மாறி மாறிக் கிடைப்பதற்கான நிகழ்தகவானது
(1) \(\frac{3}{14}\)
(2) \(\frac{5}{14}\)
(3) \(\frac{1}{14}\)
(4) \(\frac{9}{14}\)
குறிப்பு :
P(WBWBW) + P(BWBWB)

விடை :
(3) \(\frac{1}{14}\)
Question 11.
A மற்றும் B ஆகிய இரு நிகழ்ச்சிகள் AC B மற்றும் P(B) ≠ 0, என இருப்பின் பின்வருவனவற்றுள் எது மெய்யானது?
(1) P (A/B) = \(\frac{\mathrm{P}(\mathrm{A})}{\mathrm{P}(\mathrm{B})}\)
(2) P(A/B) < P(A) (3) P(A/B) ≥ P(A)mi (4) P(A/B) > P(B)
விடை :
(3) P(A/B) >P(A)
Question 12.
ஒரு பையில் 6 பச்சை, 2 வெள்ளை மற்றும் 7 கருப்பு நிற பந்துகள் உள்ளன. இரு பந்துகள் ஒரே சமயத்தில் எடுக்கும் போது அவை வெவ்வேறு நிறமாக இருப்பதற்கான நிகழ்தகவானது
(1) \(\frac{68}{105}\)
(2) \(\frac{71}{105}\)
(3) \(\frac{64}{105}\)
(4) \(\frac{73}{105}\)
குறிப்பு :

விடை :
(1) \(\frac{68}{105}\)
![]()
Question 13.
X மற்றும் Y என்ற நிகழ்ச்சிகளுக்கு P(X/Y) = \(\frac{1}{2}\), P(Y/X)= \(\frac{1}{3}\), P(X∩Y) = \(\frac{1}{6}\) எனில் P(X∪Y) -ன் மதிப்பு
(1) \(\frac{1}{3}\)
(2) \(\frac{2}{5}\)
(3) \(\frac{1}{6}\)
(4) \(\frac{2}{3}\)
குறிப்பு :
P(X/Y) = \(\frac{1}{2}\), P(Y/X)= \(\frac{1}{3}\), P(X∩Y) = \(\frac{1}{6}\)
P(X/Y) = \(\frac{P(X \cap Y)}{P(Y)}\)
⇒ \(\frac{1}{2}\) = \(\frac{\frac{1}{6}}{P(Y)}\)
⇒ P(Y) = \(\frac{1}{6}\) × 2 = \(\frac{1}{3}\)
⇒ P(Y/X) = \(\frac{1}{3}\)
⇒ \(\frac{P(X \cap Y)}{P(X)}=\frac{1}{3}\)
⇒ \(\frac{\frac{1}{6}}{P(x)}=\frac{1}{3}\)
⇒ \(\frac{\frac{1}{6}}{\frac{1}{3}}\) = P(X)
⇒ P(X) = \(\frac{1}{6} \times \frac{3}{1}=\frac{1}{2}\)
P(X∪Y) = P(X) + P(Y) – P(X∩Y)
⇒ P(X∪Y) = \(\frac{1}{2}+\frac{1}{3}-\frac{1}{6}\)
= \(\frac{3+2-1}{6}=\frac{4}{6}=\frac{2}{3}\)
விடை :
(4) \(\frac{2}{3}\)
Question 14.
ஒரு ஜாடியில் 5 சிவப்பு மற்றும் 5 கருப்பு நிறபந்துகள் உள்ளன. ஜாடியிலிருந்து : சமவாய்ப்பு முறையில ஒரு பந்து எடுக்கப்படுகிறது. அதனையும் அதன் நிறமுள்ள மேலும் இரு பந்துகளும் ஜாடியில் மீண்டும் வைக்கப்படுகின்றன. பின்னர் ஜாடியிலிருந்து ஒரு பந்து எடுக்கப்படும் போது அது சிவப்பு நிறப் பந்தாக இருப்பதற்கான நிகழ்தகவானது.
(1) \(\frac{5}{12}\)
(2) \(\frac{1}{2}\)
(3) \(\frac{7}{12}\)
(4) \(\frac{1}{4}\)
குறிப்பு :
n(R) = 5, n(B) = 5
∴ n(S) = 10
(i) P (சிவப்பு) = \(\frac{5}{10}\) = \(\frac{1}{2}\) = P(E1)
2 பந்துகள் சிவப்பு சேர்ந்தவுடன்
P(சிவப்பு பந்துகள்) = \(\frac{7}{12}\) = P(A/E1)
(ii) P (கருப்பு பந்துகள்) = \(\frac{5}{10}\) = \(\frac{1}{2}\) = P(E2)
இரண்டு கருப்பு பந்துகள் சேர்ந்தவுடன்
P (சிவப்பு பந்து எடுத்தல்) = \(\frac{5}{12}\) = P(A/E2)
⇒ 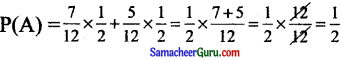
விடை :
(2) \(\frac{1}{2}\)
Question 15.
ஒன்று முதல் நூறு வரையுள்ள இயல் எண்களிலிருந்து சமவாய்ப்பு முறையில் ஒரு எண் : தேர்ந்தெடுக்கப் படுகிறது. \(\frac{(x-10)(x-50)}{x-30} \geq 0\) என்பதனைப் பூர்த்தி செய்யும் எண்ணைத் தேர்வு செய்யும் நிகழ்ச்சி A எனில், P(A)ஆனது
(1) 0.20
(2) 0.51
(3) 0.71
(4) 0.70
குறிப்பு :
முதல் 100 எண்ணிலிருந்து x ஐ தேர்வு செய்தல்
n(S) = 100
\(\frac{(x-10)(x-50)}{x-30} \geq 0\)
x = 31 லிருந்து 100 ; x = 10
∴ n(A) = {10, 31,32,33,…100} =71
∴ P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{71}{100}\) = 0.71
விடை :
(3) 0.71
![]()
Question 16.
A, B என்ற சார்பிலா நிகழ்ச்சிகளுக்கு P(A) = 0.35 மற்றும் P(A∪B) = 0.6, எனில் P(B) ஆனது
(1) \(\frac{5}{13}\)
(2) \(\frac{1}{13}\)
(3) \(\frac{4}{13}\)
(4) \(\frac{7}{13}\)
குறிப்பு : ]
A, B சார்பிலா நிகழ்ச்சிகள்
P(A∩B) = P(A). P(B)
P (A∪B) = P(A) + P(B) – P(A∩B)
⇒ 0.6 = 0.35 + P(B) – P(A). P(B)
⇒ 0.6 – 0.35 = P(B) – 0.35 P(B)
⇒ 0.25 = P(B) [1 – 0.35]
⇒ 0.25 = P(B) (0.65)
⇒ P(B) = \(\frac{0.25}{0.65}\) = \(\frac{5}{13}\)
விடை :
(1) \(\frac{5}{13}\)
Question 17.
A மற்றும் B என்ற இரு நிகழ்ச்சிகளுக்கு P(\(\overline{\mathbf{A}}\)) = \(\frac{3}{10}\) மற்றும் P(A∩\(\overline{\mathbf{B}}\)) = \(\frac{1}{2}\), எனில் P(A∩B) ன் மதிப்பு
(1) \(\frac{1}{2}\)
(2) \(\frac{1}{3}\)
(3) \(\frac{1}{4}\)
(4) \(\frac{1}{5}\)
குறிப்பு :
P(\(\overline{\mathbf{A}}\)) = \(\frac{3}{10}\)
⇒ P(A) = 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)
⇒ P(A∩ (\(\overline{\mathbf{B}}\)) = \(\frac{1}{2}\)
⇒ P(A∩ (\(\overline{\mathbf{B}}\)) = P(A) – P(A∩B)
⇒ \(\frac{1}{2}\) = \(\frac{7}{10}\) – P(A∩B)
⇒ P(A∩B) = \(\frac{7}{10}\) – \(\frac{1}{2}\)
= \(\frac{7-5}{10}\) = \(\frac{2}{10}\) = \(\frac{1}{5}\)
விடை :
(4) \(\frac{1}{5}\)
Question 18.
A மற்றும் B என்ற இரு நிகழச்சிகளுக்கு, P(A) = 0.4, P(B) = 0.8 மற்றும் P(B/A) = 0.6 , எனில் P(\(\overline{\mathbf{A}}\)∩B) -ன் மதிப்பு
(1) 0.96
(2) 0.24
(3) 0.56
(4) 0.66
குறிப்பு :
P(A) = 0.4, P(B) = 0.8, P(B/A) = 0.6
⇒ P(B/A) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}\)
⇒ 0.6 = \(\frac{P(A \cap B)}{0.4}\)
⇒ P(A∩B) = 0.24
⇒ P(A∩B) = P(B) – P(A∩B)
⇒ 0.8 – 0.24 = 0.56
விடை :
(3) 0.56
![]()
Question 19.
A, B மற்றும் C என்ற மூன்று நிகழச்சிகளில் ஒன்று மட்டுமே நிகழக்கூடும். A-க்கு சாதகமற்ற விகிதம் 7-க்கு 4 மற்றும் B-க்கு சாதகமற்ற விகிதம் 5-க்கு 3 , எனில் C-க்குச் சாதகமற்ற விகிதம்
(1) 23 : 65
(2) 65 : 23
(3) 23 : 88
(4) 88 : 23
குறிப்பு :
\(\frac{P\left(A^{\prime}\right)}{P(A)}=\frac{7}{4}\)
⇒ P(A’) = \(\frac{7}{11}\)
⇒ P(A) = \(\frac{4}{11}\)
\(\frac{\mathrm{P}\left(\mathrm{B}^{\prime}\right)}{\mathrm{P}(\mathrm{B})}=\frac{5}{3}\)⇒ P(B’) = \(\frac{5}{8}\),
P(B’) = \(\frac{3}{8}\)
A, B ,C லிருந்து ஒரே ஒரு நடக்கும் நிகழ்வுக்கான நிகழ்த கவு = P(A) + P(B) + P(C) = 1
∴ P(C) = 1 – \(\frac{3}{8}\) – \(\frac{4}{11}\)
= \(\frac{88-33-32}{88}=\frac{23}{88}\)
∴ C-க்கு சாதகமற்ற விகிதம் 65 : 23
விடை :
(2) 65 : 23
Question 20.
a மற்றும் ம-ன் மதிப்புகள் {1, 2, 3, 4} என்ற கணத்தில் திரும்ப வரும் என்ற வகையில் சமவாய்ப்பு முறையில்v தேர்ந்தெடுக்கப்பட்டால் x2 + ax + b = 0 | என்ற சமன்பாட்டின் மூலங்கள் மெய்யெண்களாக இருப்பதற்கான நிகழ்தகவு
(1) \(\frac{3}{16}\)
(2) \(\frac{5}{16}\)
(3) \(\frac{7}{16}\)
(4) \(\frac{11}{16}\)
குறிப்பு :
a, b ஆனது சமவாய்ப்பு முறையில் {1, 2, 3, 4} என்ற கணத்திலிருந்து தேர்ந்தெடுக்கப்படுகிறது.
∴ n(S) = 4 × 4 = 16
x2 + ax + b = 0
⇒ a = 1, b = a மற்றும் c = b
∴ ∆ = b2 – 4ac
= a2 – 4 (1) (b) = a2 – 4b ≥ 0
a2 – 4b ≥ 0 ஆனது
∴ A = {(2, 1) (3, 1) (4, 1) (3, 2) (4, 2) (4, 3) (4, 4)}
∴ n (A) = 7
∴ P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{7}{16}\)
விடை :
(3) \(\frac{7}{16}\)
Question 21.
A மற்றும் B என்ற இரு நிகழ்ச்சிகளுக்கு P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\), மற்றும் P(B/A) = \(\frac{2}{3}\) எனில், P(B)-ன் மதிப்பு
(1) \(\frac{1}{6}\)
(2) \(\frac{1}{3}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{1}{2}\)
குறிப்பு :
P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\), P(B/A) = \(\frac{2}{3}\)
∴ P(A/B) = \(P \frac{(A \cap B)}{P(B)}\)
P(B/A) = \(\frac{2}{3}\)
\(\frac{1}{2}\) = \(P \frac{(A \cap B)}{P(B)}\)
\(P \frac{(A \cap B)}{P(B)}\) = \(\frac{1}{4}\)
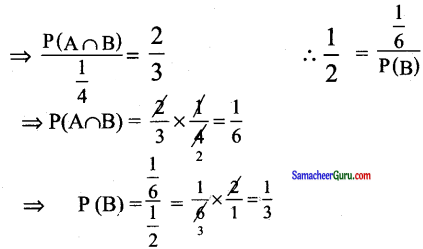
விடை :
(2) \(\frac{1}{3}\)
![]()
Question 22.
ஒரு குறிப்பிட்ட கல்லூரியில் 4% மாணவர்கள் மற்றும் 1% மாணவியர்கள் 1.8 மீட்டர் உயரத்திற்கு மேல் உள்ளனர். மேலும் கல்லூரியில் மொத்த எண்ணிக்கையில் 60% மாணவியர்கள் உள்ளனர். சமவாய்ப்பு முறையில் 1.8 மீ உயரத்திற்கு மேல் ஒருவரைத் தேர்ந்தெடுக்கும் போது அவர் மாணவியாக இருப்பதற்கான நிகழ்தகவு
(1) \(\frac{2}{11}\)
(2) \(\frac{3}{11}\)
(3) \(\frac{5}{11}\)
(4) \(\frac{7}{11}\)
குறிப்பு :
A1, A2, B என்பது, மாணவர், மாணவியர் 1.8 மீ உயரத்திற்கு மேல் ஒருவரைத் தேர்ந்தெடுக்கும் நிகழ்ச்சி என்க.
P(A1) = 1 – \(\frac{60}{100}\) = \(\frac{40}{100}\)
P(B/A1) = \(\frac{4}{100}\)
P(A2) = \(\frac{60}{100}\)
P(B/A2) = \(\frac{1}{100}\)
P(B) = P(A1) . P(B/A1) + P (A2) . P(B/A2)

விடை :
(2) \(\frac{3}{11}\)
Question 23.
பந்து நாணயங்களைச் சுண்டும் போது குறைந்தது 8 தலைகள் கிடைப்பதற்கான நிகழ்வு
(1) \(\frac{7}{64}\)
(2) \(\frac{7}{32}\)
(3) \(\frac{7}{16}\)
(4) \(\frac{7}{128}\)
குறிப்பு :
n(A) = \({ }^{10} \mathrm{C}_{8}+{ }^{10} \mathrm{C}_{9}+{ }^{10} \mathrm{C}_{10}\)
= \({ }^{10} \mathrm{C}_{2}+{ }^{10} \mathrm{C}_{1}+{ }^{10} \mathrm{C}_{0}\) [∵ \({ }^{n} \mathrm{C}_{r}={ }^{n} \mathrm{C}_{n-r}\)]
= \(\frac{10 \times 9}{2 \times 1}\) + 10 + 1 = 45 + 11 = 56
n(S) = 210 = 1024
∴ P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{56}{1024}=\frac{8 \times 7}{1024}=\frac{7}{128}\)
விடை :
(4) \(\frac{7}{128}\)
Question 24.
A மற்றும் B என்ற இரு நிகழ்ச்சிகள் நிகழ்வதற்கான நிகழ்தகவு முறையே 0.3 மற்றும் 0.6 ஆகும். A மற்றும் B ஒரே சமயத்தில் நிகழ்வதற்கான நிகழ்தகவு 0.18 எனில் A அல்லது B நிகழாமல் இருப்பதற்கான நிகழ்தகவு
(1) 0.1
(2) 0.72
(3) 0.42
(4) 0.28
குறிப்பு :
P(A) = 0.3, P(B) = 0.6, P(A∩B) = 0.18
P(\(\overline{\mathrm{A}}\)∩\(\overline{\mathrm{B}}\)) = P(\(\overline{\mathrm{A} \cup \mathrm{B}}\)) = 1 – P(A∪B)
= 1 – [P(A) + P(B) – P(A∩B)]
= 1 – (0.3 + 0.6 – 0.18)
= 1 – [0.9 – 0.18]
= 1 – [0.72] = 0.28
விடை :
(4) 0.28
![]()
Question 25.
ஒரு எண் 1 ஆனது m ≤ 5, எனில் இருபடிச் சமன்பாடு 2x2 + 2mx + m + 1 = 0 -ன் மூலங்கள் மெய்யெண்களாக இருப்பதற்கான நிகழ்தகவு
(1) \(\frac{1}{5}\)
(2) \(\frac{2}{5}\)
(3) \(\frac{3}{5}\)
(4) \(\frac{4}{5}\)
குறிப்பு :
2x2 + 2mx +m + 1 = 0
a = 2, b = 2m, c = m + 1
∴ b2 – 4ac = (2m)2 – 4 (2) (m + 1)
= 4m2 – 8 (m + 1)
= 4m2 – 8m – 8
= 4 (m2 – 2m – 2)
b2 – 4ac ≥ 0 =
⇒ 4m2 – 8m – 8 ≥ 0
⇒ m2 – 2m – 2 ≥ 0
m = 3 அல்லது 4 அல்லது 5 சமன்பாட்டை நிறைவு செய்யும்
n (A) = 3; n(S) = 5
P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{3}{5}\)
விடை :
(3) \(\frac{3}{5}\)