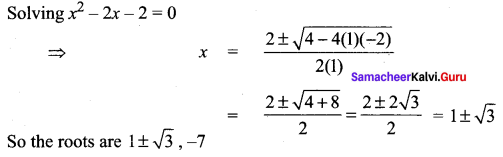You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.7
Question 1.
Factorize: x4 + 1. (Hint: Try completing the square.)
Solution:
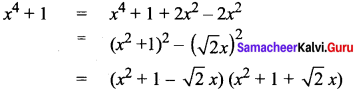
![]()
Question 2.
If x2 + x + 1 is a factor of the polynomial 3x3 + 8x2 + 8x + a, then find the value of a.
Solution:
Let 3x3 + 8x2 + 8x + a = (x2 + x + 1) (3x + a) .
Equating coefficient of x
8 = a + 3
8 – 3 = a
a = 5
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.7 Additional Questions Solved
Question 1.
Solve for x2 – 7x3 + 8x2 + 8x – 8 = 0. given 3 – \(\sqrt{5}\) is a root
Solution:
when 3 – \(\sqrt{5}\) is a root, 3 + \(\sqrt{5}\) is the other root.
S.o.r. = (3 – \(\sqrt{5}\)) + (3 + \(\sqrt{5}\)) = 6
![]()
The equation is x2 – 6x + 4 = 0
Now x4 – 7x3 + 8x2 + 8x – 8 = (x2 – 6x + 4) (x2 + px – 2)
Equating co-eff of x
12 + 4p = 8
4p = 8 – 12 = -4
So the other factor is x2 – x – 2
Now solving x2 – x – 2 = 0
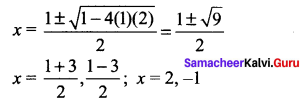
![]()
Question 2.
Solve the equation x3 + 5x2 – 16x – 14 = 0. given x + 7 is a root
Solution:
x3 + 5x2 – 16x – 14 = (x + 7) (x2 + px – 2)
Equating co-eff of x
7p – 2 = -16
7p = -16 + 2 = -14
⇒ p = -2
So the other factor is x2 – 2x – 2