Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.12

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.12

Choose the correct answer or most suitable answer:

Question 1.

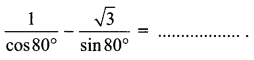
(a) \(\sqrt{2}\)
(b) \(\sqrt{3}\)
(c) 2
(d) 4
Solution:
(d) 4
Hint:

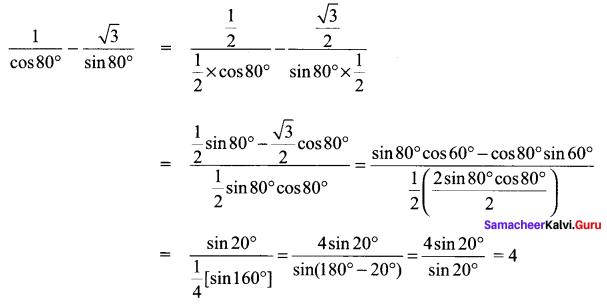
Question 2.
If cos 28° + sin 28° = k³, then cos 17° is equal to …….

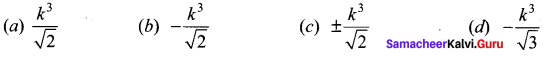
Solution:
(a) \(\frac{k^{3}}{\sqrt{2}}\)
Hint:

Question 3.

(a) 4 + \(\sqrt{2}\)
(b) 3 + \(\sqrt{2}\)
(c) 9
(d) 4
Solution:
(a) 4 + \(\sqrt{2}\)
Hint:

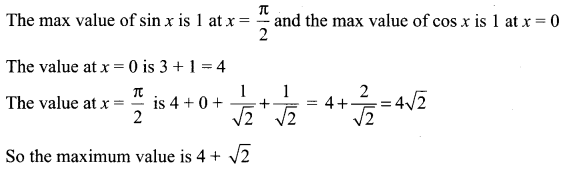
Question 4.

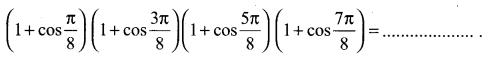
Solution:
(a) \(\frac{1}{8}\)
Hint:

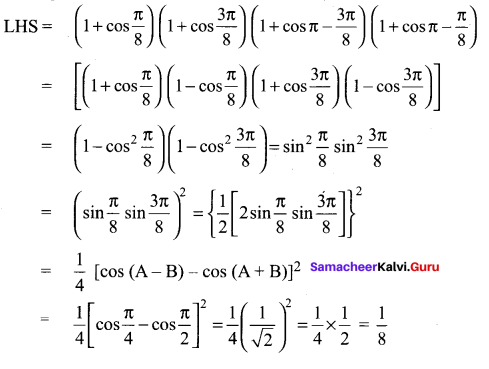
Question 5.

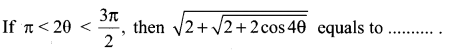
Solution:
(c) 2 cos θ
Hint:

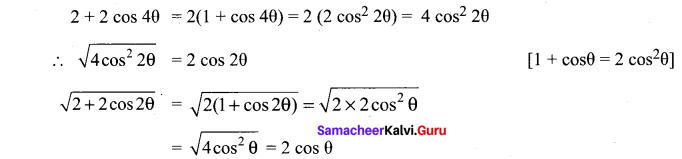
Here θ is in II Quadrant

Question 6.

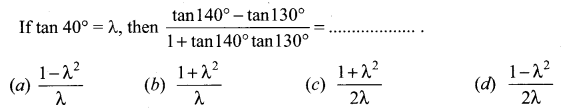
Solution:
(d) \(\text { (d) } \frac{1-\lambda^{2}}{2 \lambda}\)
Hint:

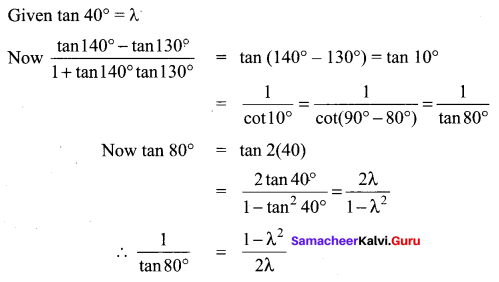
Question 7.
cos 1° + cos 2° + cos 3° + …. + cos 179° = …….
(a) 0
(b) 1
(c) -1
(d) 89
Solution:
(a) 0
Hint:
LHS = (cos 10 + cos 179°)+(cos 2° ÷ cos 178°)+ ….. +cos(89° + cos 91°)+cos 90°
cos 179° = cos (180° – 1) = – cos 1°
cos 178° = cos(180° – 2)= – cos 2°
So (cos 1°- cos 1°)+(cos 2° – cos 2°) + (cos 89° – cos 89°) + cos 90°
= 0 + 0 …. + 0 + 0 = 0.

Question 8.

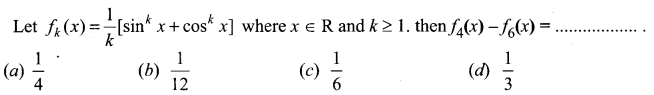
Solution:
(b) \(\frac{1}{12}\)
Hint:

Question 9.
Which of the following is not true?

Solution:
(d) sec θ = \(\frac{1}{4}\)
Hint:
sec θ = \(\frac{1}{4}\) ⇒ cos θ = 4, which is not true.

Question 10.
cos 2θ cos 2ϕ+ sin² (θ – ϕ) – sin² (θ + ϕ) is equal to …….
(a) sin 2(θ + ϕ)
(b) cos 2(θ + ϕ)
(c) sin 2(θ – ϕ)
(d) cos 2(θ – ϕ)
Solution:
(b) cos 2(θ + ϕ)
Hint.
Given cos 2θ . cos 2ϕ + sin² (θ – ϕ) – sin² (θ + ϕ)
= cos 2θ cos 2ϕ + sin (θ – ϕ + θ + ϕ) sin (θ – ϕ – θ – ϕ)
= cos 2θ cos 2ϕ + sin 2θ sin(-2ϕ)
= cos 2θ cos 2ϕ – sin 2θ sin(2ϕ)
= cos (2θ + 2ϕ) = cos 2(θ + ϕ)

Question 11.

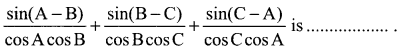
(a) sin A + sin B + sin C
(b) 1
(c) 0
(d) cos A + cos B + cos C
Solution:
(c) 0
Hint:

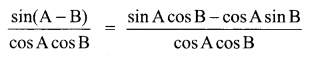
= tan A – tan B

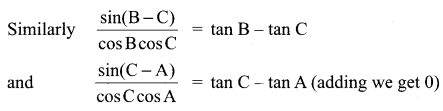
Question 12.
cos pθ + cos qθ = 0 and if p ≠ q, then 0 is equal to (n is any integer) …….

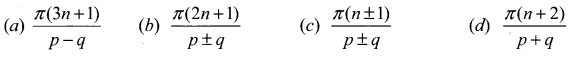
Solution:
(b) \(\frac{\pi(2 n+1)}{p \pm q}\)
Hint:
cos pθ + cos qθ = 0

Question 13.
If tan α and tan β are the roots x² + ax + b = 0, then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to …….
Solution:
(b) \(\frac{a}{b}\)
Hint:
tan² x + a tan x + b = 0
α and β are the roots of the equation
⇒ tan² α + a tan α + b = 0 ….. (1)
tan² β + a tan β + b = 0 …… (2)
(1) – (2) => tan² α – tan² β + a (tan α – tan β) = 0
(tan α – tan β) (tan α + tan β) + a (tan α – tan β) = 0
⇒ tan α + tan β = – a …. (A)
(1) × tan β – (2) × tan α

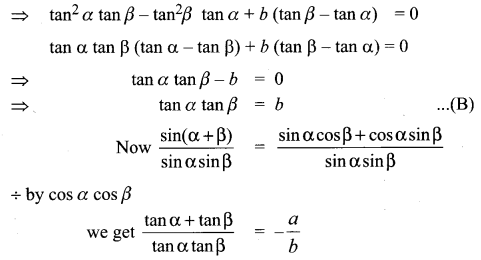
Question 14.
In a triangle ABC, sin² A + sin² B + sin² C = 2, then the triangle is …….
(a) equilateral triangle
(b) isosceles triangle
(c) right triangle
(d) scalene triangle
Solution:
(c) right triangle
Hint.
On simplifying we get
sin² A + sin² B + sin² C = 2 + 2 cos A cos B cos C
= 2 (given)
⇒ cos A cos B cos C = 0
cos A (or) cos B (or) cos C = 0
⇒ A (or) B (or) C = π/2
⇒ ABC (is a right angled triangle).

Question 15.
If f(θ) = |sin θ| + |cos θ|, θ ∈ R, then f(θ) is in the interval …….
(a) [0, 2]
(b) [1, \(\sqrt{2}\)]
(c) [1, 2]
(d) [0, 1]
Solution:
(b) [1, \(\sqrt{2}\)]
Hint:

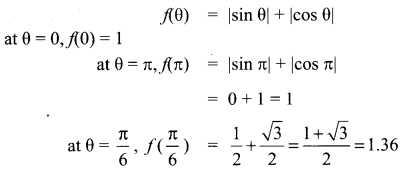
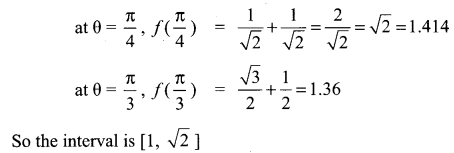
Question 16.

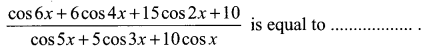
Solution:
Nr: cos 6x + cos 4x + 5 cos 4x + 5 cos 2x + 10 cos 2x + 10
= 2 cos 5x cos x+5(2 cos 3x cos x)+ 10(2 cos²x)
= 2 cos x [cos 5x + 5 cos 3x + 10 cos x]

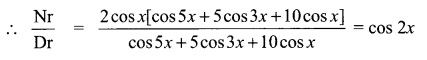
Question 17.
The triangle of maximum area with constant perimeter 12m
(a) is an equilateral triangle with side 4m
(b) is an isosceles triangle with sides 2m, 5m, 5m
(c) is a triangle with sides 3m, 4m, 5m
(d) does not exists
Solution:
(a) is an equilateral triangle with side 4m
Hint.
A triangle will have a max area (with a given perimeter) when it is an equilateral triangle.

Question 18.
A wheel is spinning at 2 radians/second. How many seconds will it take to make 10 complete rotations?
(a) 10π seconds
(b) 20π seconds
(c) 5π seconds
(d) 15π seconds
Solution:
(a) 10π seconds
Hint.
1 rotation makes 2π^c
Distance travelled in 1 second = 2 radians
So time taken to complete 10 rotations = 6 × 2π = 20 π^c
\(=\frac{20 \pi}{2}=10 \pi\) seconds

Question 19.
If sin α + cos α = b, then sin 2α is equal to ……..

Solution:
(b) b² – 1, if b > \(\sqrt{2}\)
Hint:
sin α + cos β = b
(sin α + cos β)² = b²
sin² α + cos² α + 2 sin α cos α = b²
sin² α = b² – 1

Question 20.

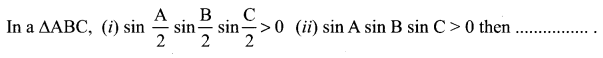
(a) Both (i) and (ii) are true
(b) Only (i) is true
(c) Only (ii) is true
(d) Neither (i) nor (ii) is true
Solution:
(a) Both (i) and (ii) are true
Hint.
When A + B + C = 180°

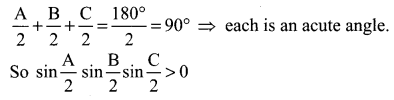
When A + B + C = 180° each angle will be lesser than 180°
So sin A, sin B, sin C > 0
⇒ sin A sin B sin C > 0
So both (i) and (ii) are true