Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.6

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.6

Choose the correct or the most suitable answer from the given four alternatives
Question 1.

(a) 1
(b) 0
(c) ∞
(d) -∞
Solution:
(b) 0

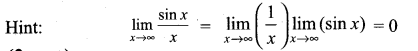
Question 2.

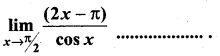
(a) 2
(b) 1
(c) -2
(d) 0
Solution:
(c) -2

Question 3.

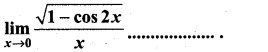
(a) 0
(b) 1
(c) 2
(d) does not exist
Solution:
(d) does not exist

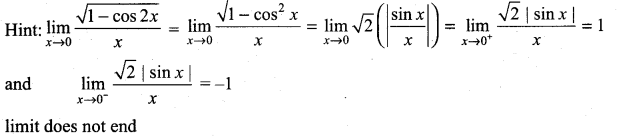
Question 4.

(a) 1
(b) -1
(c) 0
(d) 2
Solution:
(a) 1

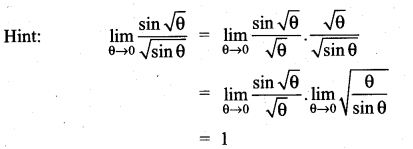
Question 5.

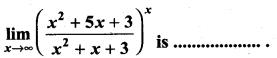
(a) e⁴
(b) e²
(c) e³
(d) 1
Solution:
(a) e⁴

Question 6.

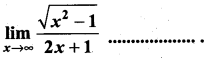
(a) 1
(b) 0
(c) -1
(d) \(\frac{1}{2}\)
Solution:
(d) \(\frac{1}{2}\)

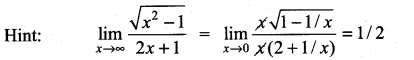
Question 7.

(a) log ab
(b) log \(\left(\frac{a}{b}\right)\)
(c) log \(\left(\frac{b}{a}\right)\)
(d) \(\frac{a}{b}\)
Solution:
(b) log \(\left(\frac{a}{b}\right)\)

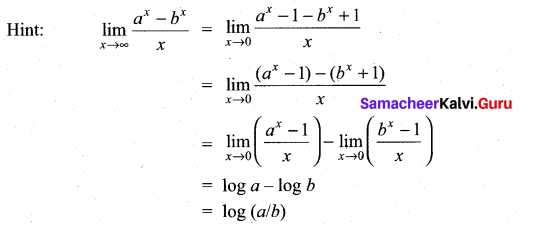
Question 8.

(a) 2 log 2
(b) 2 (log 2)²
(c) log 2
(d) 3 log 2
Solution:
(b) 2 (log 2))²

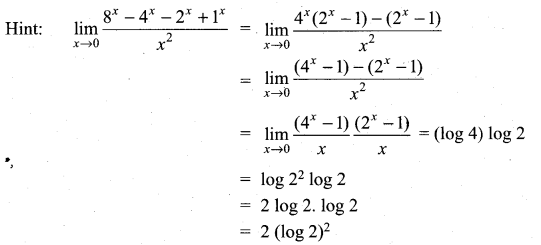
Question 9.
If f(x) = \(x(-1)^{ \left\lfloor \frac { 1 }{ x } \right\rfloor }\), x ≤ θ, then the value of is equal to …………….
(a) -1
(b) 0
(c) 2
(d) 4
Solution:
(b) 0

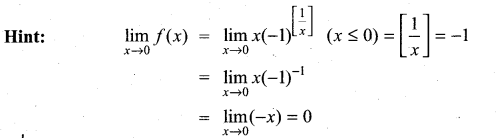
Question 10.

(a) 2
(b) 3
(c) does not exist
(d) 0
Solution:
(c) does not exist

Limit does not exist

Question 11.
Let the function f be defined f(x) = 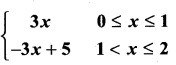then ……………

Solution:

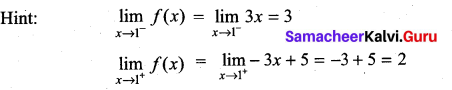
Limit does not exist

Question 12.
If f: R → R is defined by f(x) = \(\lfloor x-3\rfloor+|x-4|\) for x ∈ R, then
is equal to …………..
(a) -2
(b) -1
(c) 0
(d) 1
Solution:
(c) 0

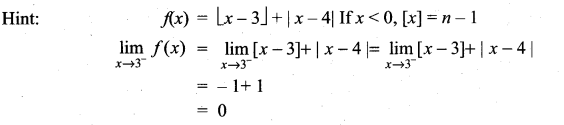
Question 13.

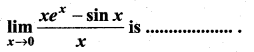
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(d) 0

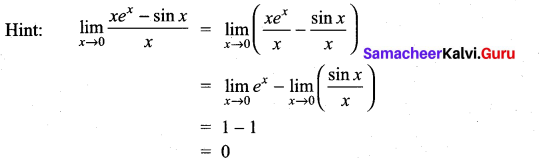
Question 14.
If then the value of p is ………….
(a) 6
(b) 9
(c) 12
(d) 4
Solution:
(c) 12

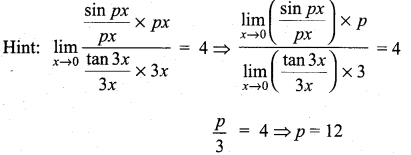
Question 15.

(a) \(\sqrt{2}\)
(b) \(\frac{1}{\sqrt{2}}\)
(c) 1
(d) 2
Solution:
(a) \(\sqrt{2}\)

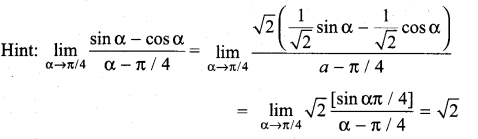
Question 16.

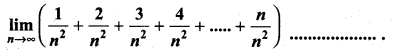
(a) \(\frac{1}{2}\)
(b) 0
(c) 1
(d) ∞
Solution:
(a) \(\frac{1}{2}\)

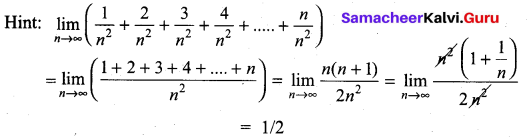
Question 17.

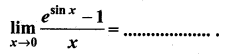
(a) 1
(b) e
(c) \(\frac{1}{e}\)
(d) 0
Solution:
(a) 1

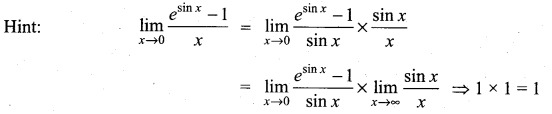
Question 18.

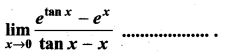
(a) 1
(b) e
(c) \(\frac{1}{2}\)
(d) 0
Solution:
(a) 1

Question 19.
The value of 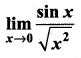is ……………
(a) 1
(b) -1
(c) 0
(d) ∞
Solution:
(d) ∞
Hint:

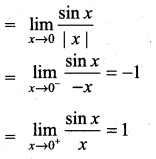
So limit does not exist

Question 20.
The value of where k is an integer is …………..
(a) -1
(b) 1
(c) 0
(d) 2
Solution:
(b) 1

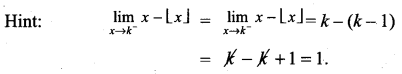
Question 21.
At x = \(\frac{3}{2}\) the function f(x) = \(\frac{|2 x-3|}{2 x-3}\) is ………….
(a) Continuous
(b) discontinuous
(c) Differentiate
(d) non-zero
Solution:
(b) discontinuous

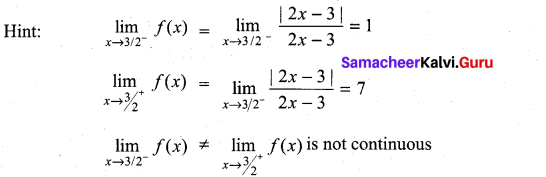
Question 22.
Let f: R → R be defined by f(x) = 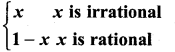then f is ……………
(a) Discontinuous at x = \(\frac{1}{2}\)
(b) Continuous at x = \(\frac{1}{2}\)
(c) Continuous everywhere
(d) Discontinuous everywhere
Solution:
(b) Continuous at x = \(\frac{1}{2}\)

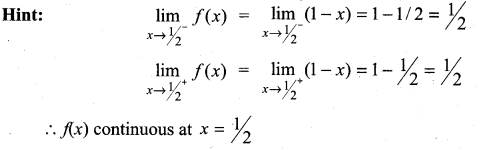
Question 23.
The function f(x) = 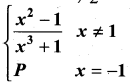is not defined for x = -1. The value of f(-1) so that the function extended by this value is continuous is …………..
(a) \(\frac{2}{3}\)
(b) \(-\frac{2}{3}\)
(c) 1
(d) 0
Solution:
(b) \(-\frac{2}{3}\)
Hint: For the function to be continuous at x = 1

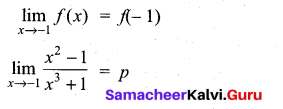
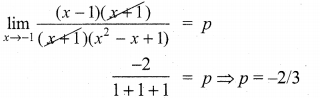
Question 24.
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f(4.5) is equal to ……………
(a) \(\frac{f(3)+f(4.5)}{7.5}\)
(b) 12
(c) 17.5
(d) \(\frac{f(4.5)-f(3)}{1.5}\)
Solution:
(b) 12

Question 25.
Let a function f be defined by f(x) = \(\frac{x-|x|}{x}\) for x ≠ 0 and f(0) = 2. Then f is …………..
(a) Continuous nowhere
(b) Continuous everywhere
(c) Continuous for all x except x = 1
(d) Continuous for all x except x = 0
Solution:
(d) Continuous for all x except x = 0
Hint:

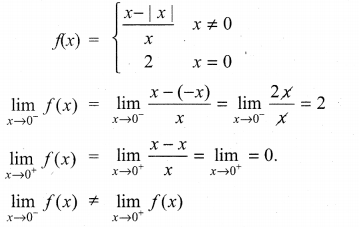
∴ f(x) is not continuous at x = 0
⇒ f(x) is continuous for all except x = 0