Students can download 12th Business Maths Chapter 5 Numerical Methods Ex 5.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.3
Choose the correct answer.
Question 1.
∆2 y0 = ______
(a) y2 – 2y1 + y0
(b) y2 + 2y1 – y0
(c) y2 + 2y1 + y0
(d) y2 – y1 + 2y0
Answer:
(a) y2 – 2y1 + y0
Hint:
∆2 y0 = ∆(∆y0) = ∆(y1 – y0) = ∆y1 – ∆y0
= (y2 – y1) – (y1 – y0)
= y2 – 2y1 + y0
Question 2.
∆f(x) = _______
(a) f(x + h)
(b) f(x) – f(x + h)
(c) f(x + h) – f(x)
(d) f(x) – f(x – h)
Answer:
(c) f(x + h) – f(x)
Hint:
∆f(x) = f(x + h) – f(x)
![]()
Question 3.
E = ______
(a) 1 + ∆
(b) 1 – ∆
(c) 1 + ∇
(d) 1 – ∇
Answer:
(a) 1 + ∆
Hint:
E = 1 + ∆
Question 4.
If h = 1, then ∆(x2) = ________
(a) 2x
(b) 2x – 1
(c) 2x + 1
(d) 1
Answer:
(c) 2x + 1
Hint:
∆(x2) = (x + h)2 – x2 = (x + 1)2 – x2 = 2x + 1
![]()
Question 5.
If c is a constant then ∆c = ______
(a) c
(b) ∆
(c) ∆2
(d) 0
Answer:
(d) 0
Question 6.
If m and n are positive integers then ∆m ∆n f(x) = _______
(a) ∆m+n f(x)
(b) ∆m f(x)
(c) ∆n f(x)
(d) ∆m-n f(x)
Answer:
(a) ∆m+n f(x)
![]()
Question 7.
If ‘n’ is a positive integer ∆n [∆-n f(x)] _______
(a) f(2x)
(b) f(x + h)
(c) f(x)
(d) ∆ f(2x)
Answer:
(c) f(x)
Question 8.
E f(x) = _______
(a) f(x – h)
(b) f(x)
(c) f(x + h)
(d) f(x + 2h)
Answer:
(c) f(x + h)
![]()
Question 9.
∇ = _______
(a) 1 + E
(b) 1 – E
(c) 1 – E-1
(d) 1 + E-1
Answer:
(c) 1 – E-1
Question 10.
∇ f(a) = ______
(a) f(a) + f(a – h)
(b) f(a) – f(a + h)
(c) f(a) – f(a – h)
(d) f(a)
Answer:
(c) f(a) – f(a – h)
![]()
Question 11.
For the given points (x0 , y0) and (x1, y1) the Lagrange’s formula is ______
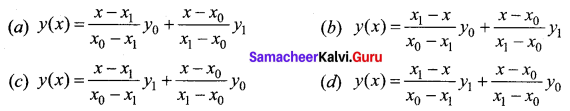
Answer:
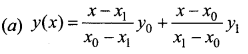
Question 12.
Lagrange’s interpolation formula can be used for ________
(a) equal intervals only
(b) unequal intervals only
(c) both equal and unequal intervals
(d) none of these
Answer:
(c) both equal and unequal intervals
![]()
Question 13.
If f(x) = x2 + 2x + 2 and the interval of differencing is unity then ∆ f(x) _______
(a) 2x – 3
(b) 2x + 3
(c) x + 3
(d) x – 3
Answer:
(b) 2x + 3
Hint:
f(x) = 2x2 + 2x + 2
h = 1
∆f(x) = (x + 1)2 + 2(x + 1) + 2 – x2 – 2x – 2
= x2 + 2x + 1 +2x + 2 + 2 – x2 – 2x – 2
= 2x + 3
Question 14.
For the given data find the value of ∆3 y0 is _________
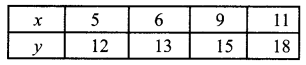
(a) 1
(b) 0
(c) 2
(d) -1
Answer:
(b) 0
Hint:
