Samacheer Kalvi 12th Computer Science Solutions Chapter 4 Algorithmic Strategies

Students can Download Computer Science Chapter 4 Algorithmic Strategies Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 4 Algorithmic Strategies

Samacheer Kalvi 12th Computer Science Algorithmic Strategies Text Book Back Questions and Answers

PART – I
I. Choose The Best Answer

Question 1.
The word comes from the name of a Persian mathematician Abu Jafar Mohammed ibn – i Musa al Khowarizmi is called?
(a) Flow chart
(b) Flow
(c) Algorithm
(d) Syntax
Answer:
(c) Algorithm

Question 2.
From the following sorting algorithms which algorithm needs the minimum number of swaps?
(a) Bubble sort
(b) Quick sort
(c) Merge sort
(d) Selection sort
Answer:
(d) Selection sort

Question 3.
Two main measures for the efficiency of an algorithm are ……………………………
(a) Processor and memory
(b) Complexity and capacity
(c) Time and space
(d) Data and space
Answer:
(c) Time and space

Question 4.
The complexity of linear search algorithm is ……………………………
(a) O(n)
(b) O(log n)
(c) O(n2)
(d) O(n log n)
Answer:
(a) O(n)

Question 5.
From the following sorting algorithms which has the lowest worst case complexity?
(a) Bubble sort
(b) Quick sort
(c) Merge sort
(d) Selection sort
Answer:
(c) Merge sort

Question 6.
Which of the following is not a stable sorting algorithm?
(a) Insertion sort
(b) Selection sort
(c) Bubble sort
(d) Merge sort
Answer:
(b) Selection sort

Question 7.
Time complexity of bubble sort in best case is ……………………………
(a) θ(n)
(b) θ(n log n)
(c) θ(n2)
(d) θ(n(logn) 2)
Answer:
(a) θ(n)

Question 8.
The \(\Theta\) notation in asymptotic evaluation represents
(a) Base case
(b) Average case
(c) Worst case
(d) NULL case
Answer:
(b) Average case

Question 9.
If a problem can be broken into subproblems which are reused several times, the problem possesses which property?
Answer:
(a) Overlapping subproblems
(b) Optimal substructure
(c) Memoization
(d) Greedy
Answer:
(a) Overlapping subproblems

Question 10.
In dynamic programming, the technique of storing the previously calculated values is called?
(a) Saving value property
(b) Storing value property
(c) Memoization
(d) Mapping
Answer:
(c) Memoization

PART – II
II. Answer The Following Questions

Question 1.
What is an Algorithm?
Answer:

• An algorithm is a finite set of instructions to accomplish a particular task.
• It is a step-by-step procedure for solving a given problem.

Question 2.
Define Pseudocode?
Answer:

1. Pseudocode is a mix of programming – language – like constructs and Plain English.
2. Pseudocode is a notation similar to programming languages. Algorithms expressed in pseudo-code are not intended to be executed by computers, but for communication among people.

Question 3.
Who is an Algorist?
Answer:

1. A person skilled in the design of algorithms are called an Algorist.
2. An algorithmic artist.

Question 4.
What is Sorting?
Answer:
Sorting is the process of arranging information or data in certain order either in ascending or descending.

Question 5.
What is searching? Write its types?
Answer:
A search algorithm is a step-by-step procedure used to locate specific data among a collection of data. Types of searching algorithms are

1. Linear search
2. Binary search
3. Hash Search
4. Binary Tree search

PART – III
III. Answer The Following Questions

Question 1.
List the characteristics of an algorithm?
Answer:

• Input
• Output
• Finiteness
• Effectiveness
• Correctness
• Simplicity
• Unambiguous
• Feasibility
• Portable
• Independent

Question 2.
Discuss Algorithmic complexity and its types?
Answer:
The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.

Time Complexity:
The Time complexity of an algorithm is given by the number of steps taken by the algorithm to complete the process.

Space Complexity:
Space complexity of an algorithm is the amount of memory required to run to its completion.

Question 3.
What are the factors that influence time and space complexity?
Answer:
The factors that influence time and space complexity are

1. Time
2. Space

Time Factor:
Time is measured by counting the number of key operations like comparisons in the sorting algorithm.
Space Factor:
Space is measured by the maximum memory space required by the algorithm.

Question 4.
Write a note on Asymptotic notation?
Answer:
Asymptotic Notations:
Asymptotic Notations are languages that use meaningful statements about time and space complexity.

(I) Big O
Big O is often used to describe the worst – case of an algorithm.

(II) Big Ω
Big Omega is the reverse Big O, if Big O is used to describe the upper bound (worst – case) of an asymptotic function, Big Omega is used to describe the lower bound (best-case).

(III) Big \(\Theta\)
When an algorithm has complexity with lower bound = upper bound, say that an algorithm has a complexity O (n log n) and Ω (n log n), it actually has the complexity \(\Theta\) (n log n), which means the running time of that algorithm always falls in n log n in the best – case and worst – case.

Question 5.
What do you understand by Dynamic programming?
Answer:

• Dynamic programming is an algorithmic design method that can be used when the solution to a problem can be viewed as the result of a sequence of decisions.
• The dynamic programming approach is similar to divide and conquer. The given problem is divided into smaller and yet smaller possible sub-problems.
• Dynamic programming is used whenever problems can be divided into similar sub-problems. So that their results can be re-used to complete the process.
• Dynamic programming approaches are used to find the solution in an optimized way.
• For every inner sub-problem, the dynamic algorithm will try to check the results 0 the previously solved sub-problems.
• The solutions of overlapped sub-problems are combined in order to get a better solution.

PART – IV
IV. Answer The Following Questions

Question 1.
Explain the characteristics of an algorithm?
Answer:

1. Input – Zero or more quantities to be supplied.
2. Output – At least one quantity is produced.
3. Finiteness – Algorithms must terminate after finite number of steps.
4. Definiteness – All operations should be well defined. For example operations involving division by zero or taking square root for negative number are unacceptable.
5. Effectiveness – Every instruction must be carried out effectively.
6. Correctness – The algorithms should be error-free.
7. Simplicity – Easy to implement.
8. Unambiguous – Algorithm should be clear and unambiguous. Each of its steps and their inputs/outputs should be clear and must lead to only one meaning.
9. Feasibility – Should be feasible with the available resources.
10. Portable – An algorithm should be generic, independent of any programming language or an operating system able to handle all range of inputs.
11. Independent – An algorithm should have step-by-step directions, which should be independent of any programming code.

Question 2.
Discuss the Linear search algorithm.?
Answer:
Linear Search:
Linear search also called sequential search is a sequential method for finding a particular value in a list. This method checks the search element with each element in sequence until the desired element is found or the list is exhausted. In this searching algorithm, a list need not be ordered.

Pseudocode:
(I) Traverse the array using for loop
(II) In every iteration, compare the target search key value with the current value of the list.

1. If the values match, display the current index and value of the array
2. If the values do not match, move on to the next array element.

(III) If no match is found, display the search element not found.
To search the number 25 in the array given below, linear search will go step by step in a sequential order starting from the first element in the given array if the search element is found that index is returned otherwise the search is continued till the last index of the array. In this example number 25 is found at index number 3.

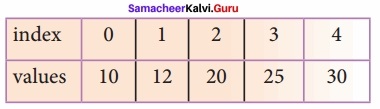
Example 1:
Input: values[ ] = {5, 34, 65, 12, 77, 35}
target = 77
Output: 4
Example 2:
Input: values[ ] = {101, 392, 1, 54, 32, 22, 90, 93}
target = 200
Output: -1 (not found)

Question 3.
What is Binary search? Discuss with example?
Answer:
Binary Search:
Binary search also called a half-interval search algorithm. It finds the position of a search element within a sorted array. The binary search algorithm can be done as a divide-and-conquer search algorithm and executes in logarithmic time.

Pseudocode for Binary search:
(I) Start with the middle element:

• If the search element is equal to the middle element of the array i.e., the middle value = number of elements in array/2, then return the index of the middle element.
• If not, then compare the middle element with the search value,
• If the search element is greater than the number in the middle index, then select the elements to the right side of the middle index, and go to Step-1.
• If the search element is less than the number in the middle index, then select the elements to the left side f the middle index, and start with Step-1.

(II) When a match is found, display a success message with the index of the element matched.
(III) If no match is found for all comparisons, then display an unsuccessful message.

Binary Search Working principles:
List of elements in an array must be sorted first for Binary search. The following example describes the step by step operation of binary search. Consider the following array of elements, the array is being sorted so it enables to do the binary search algorithm. Let us assume that the search element is 60 and we need to search the location or index of search element 60 using binary search.

First, we find index of middle element of the array by using this formula:
mid = low + (high – low) / 2
Here it is, 0 + (9 – 0 ) / 2 = 4 (fractional part ignored). So, 4 is the mid value of the array.

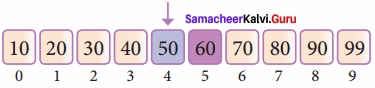
Now compare the search element with the value stored at mid-value location 4. The value stored at the location or index 4 is 50, which is not match with search element. As the search value of 60 is greater than 50.

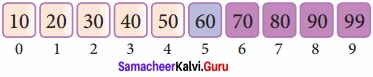
Now we change our low to mid + 1 and find the new mid-value again using the formula, low to mid – 1
mid = low + (high – low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.

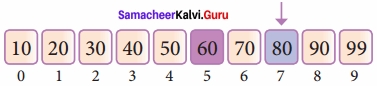
The value stored at location or index 7 is not a match with the search element, rather it is more than what we are looking for. So, the search element must be in the lower part from the current mid-value location

The search element still not found. Hence, we calculated the mid again by using the formula.
high = mid – 1
mid = low + (high – low) / 2
Now the mid-value is 5.

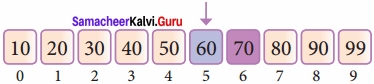
Now we compare the value stored at location 5 with our search element. We found that it is a match.

We can conclude that the search element 60 is found at the location or index 5. For example, if we take the search element as 95, For this value this binary search algorithm returns the unsuccessful result.

Question 4.
Explain the Bubble sort algorithm with an example?
Answer:
Bubble sort algorithm:
Bubble sort is a simple sorting algorithm. The algorithm starts at the beginning of the list of values stored in an array. It compares each pair of adjacent elements and swaps them if they are in the unsorted order. This comparison and passed to be continued until no swaps are needed, which indicates that the list of values stored in an array is sorted. The algorithm is a comparison sort, is named for the way smaller elements “bubble” to the top of the list.

Although the algorithm is simple, it is too slow and less efficient when compared to insertion sort and other sorting methods. Assume list is an array of n elements. The swap function swaps the values of the given array elements.

Pseudo code:

1. Start with the fist element i.e., index = 0, compare the current element with the next element of the array.
2. If the current element is greater than the next element of the array, swap them.
3. If the current element is less than the next or right side of the element, move to the next element. Go to Step 1 and repeat until end of the index is reached.

Let’s consider an array with values {15, 11, 16, 12, 14, 13} Below, we have a pictorial representation of how bubble sort will sort the given array.

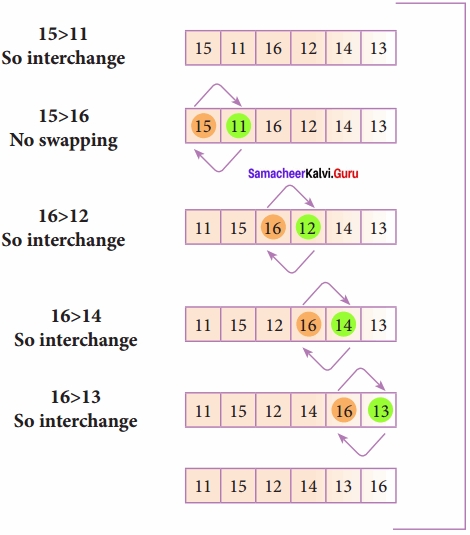
The above pictorial example is for iteration – 1. Similarly, remaining iteration can be done. The final iteration will give the sorted array.
At the end of all the iterations we will get the sorted values in an array as given below:

Question 5.
Explain the concept of Dynamic programming with a suitable example?
Answer:

• Dynamic programming is an algorithmic design method that can be used when the solution to a problem can be viewed as the result of a sequence of decisions.
• Dynamic programming approach is similar to divide and conquer. The given problem is divided into smaller and yet smaller possible sub-problems.
• Dynamic programming is used whenever problems can be divided into similar sub-problems. So that their results can be re-used to complete the process.
• Dynamic programming approaches are used to find the solution in optimized way.
• For every inner sub-problem, dynamic algorithm will try to check the results 0 the previously solved sub-problems.
• The solutions of overlapped sub-problems are combined in order to get the better solution.

Steps to do Dynamic programming:

• The given problem will be divided into smaller overlapping sub-problems.
• An optimum solution for the given problem can be achieved by using result of smaller sub-problems.
• Dynamic algorithms use Memoization.

Fibonacci Series – An example:

• Fibonacci series generates the subsequent number by adding two previous numbers.
• Fibonacci series starts from two numbers – Fib 0 & Fib 1. The initial values of Fib 0 &.
  Fib 1 can be taken as 0 and 1.
  Fibonacci series satisfies the following conditions:
  Fibn = Fib_n-1n , + Fib _n-2,
  Hence, a Fibonacci series for the n value 8 can look like this
  Fib₈ = 0 1 1 2 3 5 8 1 3

Fibonacci Iterative Algorithm with Dynamic programming approach:
The following example shows a simple Dynamic programming approach for the generation of the Fibonacci series. Initialize f0 = 0, f1 = 1
Step-1: Print the initial values of Fibonacci f0 and f1
Step- 2: Calculate Fibonacci fib ← f0+ f1
Step- 3: Assign fO ← fl, fl ← fib Step- 4: Print the next consecutive value of Fibonacci fib Step- 5: Go to step-2 and repeat until the specified number of terms generated For example, if we generate Fibonacci series up to 10 digits, the algorithm will generate the series as shown below: The Fibonacci series is: 011 2 3 5 813 21 34 55. PART

Samacheer Kalvi 12th Computer Science Algorithmic Strategies Additional Questions and Answers

PART – I
I. Choose The Best Answer

Question 1.
0(1) is an example of
a) worst case
b) best case
c) Average case
d) Null case
Answer:
b) best case

Question 2.
The word Algorithm has come to refer to a method ……………………………
(a) Solve a problem
(b) Insert a data
(c) Delete data
(d) Update data
Answer:
(a) Solve a problem

Question 3.
Binary search also called
a) Half-interval search
b) Sequential search
c) Unordered search
d) Full-interval search
Answer:
a) Half-interval search

Question 4.
Complete the diagram

Answer:
Process

Question 5.
An algorithm that yields expected output for a valid input is called as ……………………………
Answer:
Algorithmic solution.

Question 6.
The program should be written for the selected language with specific ……………………………
Answer:
Syntax

Question 7.
…………………………… is an expression of the algorithm in a programming language.
Answer:
Program

Question 8.
……………. is a step-by-step procedure for solving a given problem
a) Program
b) Algorithm
c) Statements
d) Structure
Answer:
b) Algorithm

Question 9.
Which one of the following is a theoretical performance analysis of an algorithm?
(a) A posteriori testing
(b) A priori estimates
(c) A preposition
(d) A post preori
Answer:
(b) A priori estimates

Question 10.
…………………………… is called performance measurement.
(a) A posteriori testing
(b) A priori estimates
(c) A preposition
(d) A post preori
Answer:
(a) A posteriori testing

Question 11.
An algorithm that yields expected output for a valid input is called an
a) Algorithmic Structure
b) Algorithmic Solution
c) Algorithmic Strategy
d) Algorithmic Procedure
Answer:
b) Algorithmic Solution

Question 12.
Which of the following statement is true?
(a) Space Factor is the maximum memory space required by an algorithm
(b) Space Factor is the minimum memory spaces required by an algorithm
Answer:
(a) Space Factor is the maximum memory space required by an algorithm

Question 13.
In space complexity, the space required by an algorithm is equal to the sum of …………………………… part and …………………………… part.
Answer:
Fixed, Variable

Question 14.
…………………………… is an example of a variable part of space complexity.
Answer:
Recursion

Question 15.
A …………………………… or …………………………… trade-off is a way of solving in less time by using more storage space or by solving a given algorithm in very little space by spending more time.
Answer:
Space – time, time – memory

Question 16.
Which of the following component is defined as the total space required by variables, which sizes depends on the problem and its iteration?
a) Time part
b) Variable part
c) Fixed part
d) Memory part
Answer:
b) Variable part

Question 17.
How many asymptotic notations are used to represent the time complexity of algorithms?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3

Question 18.
Which of the following is not a factor used to measure the time efficiency of an algorithm?
a) Speed of the machine
b) Operating system
c) Programming language
d) Designing an algorithm
Answer:
d) Designing an algorithm

Question 19.
………………………… is the reverse of Big O.
(a) Big Ω
(b) Big \(\Theta\)
(c) Big C
(d) Big ⊗
Answer:
(a) Big Ω

Question 20.
………………………… describes the worst case of an algorithm.
(a) Big Q
(b) Big \(\Theta\)
(c) Big O
(d) Big C
Answer:
(c) Big O

Question 21.
…………………….. describes the lower bound of an algorithm.
(a) Big Ω
(b) Big \(\Theta\)
(c) Big O
(d) Big ⊗
Answer:
(a) Big Ω

Question 22.
Which search technique is also called sequential search techniques?
(a) Binary
(b) Binary Tree
(c) Hash
(d) Linear
Answer:
(d) Linear

Question 23.
What value will be returned by the linear search technique if the value is not found?
(a) 0
(b) 1
(c) -1
(d) +1
Answer:
(c) -1

Question 24.
Which search algorithm is called a Half-Interval search algorithm?
(a) Binary
(b) Binary Tree
(c) Hash
(d) Linear
Answer:
(a) Binary

Question 25.
Which technique is followed by the Binary Search algorithm?
(a) Subroutines
(b) Mapping
(c) Divide and conquer
(d) Namespaces
Answer:
(c) Divide and conquer

Question 26.
In Binary Search, if the search element is …………………….. to the middle element of the array, then the index of the middle element is returned.
(a) >
(b) <
(c) =
(d) < >
Answer:
(c) =

Question 27.
In Binary search, if the search element is greater than the number in the middle index, then select the elements to the side of the middle index.
(a) Right
(b) Left
(c) Middle
(d) Bottom
Answer:
(a) Right

Question 28.
Fill in the box [Formula for Binary Search]
mid = low + (high – low) /
Answer:
2

Question 29.
……………………… is a simple sorting algorithm.
(a) Binary
(b) Bubble
(c) Selection
(d) Insertion
Answer:
(b) Bubble

Question 30.
Which one of the following is not a characteristic of Bubble Sort?
(a) Simple
(b) Too slow
(c) Too fast
(d) Less efficient
Answer:
(c) Too fast

Question 31.
In selection sort, there will be ……………………….. exchange for every pass through the list.
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1

Question 32.
How many passes are used in the Insertion Sort to get the final sorted list?
(a) 0
(b) 1
(c) n
(d) n -1
Answer:
(d) n – 1

Question 33.
………………………….. approach is similar to divide and conquer.
Answer:
Dynamic programming

Question 34.
………………………… is an example of a dynamic programming approach.
(a) Fibonacci
(b) Prime
(c) Factorial
(d) Odd or Even
Answer:
(a) Fibonacci

Question 35.
Match the following.
(1) Linear search – (i) o(n²)
(2) Binary – (ii) o(n)
(3) Bubble Sort – (iii) o(log n)
(4) Merge Sort – (iv) o(n log n)
(a) 1 – (ii), 2 – (iii), 3 – (i), 4 – (iv)
(b) 1 – (i), 2 – (ii), 3 – (iii), 4 – (iv)
(c) 1 – (iv), 2 – (iii), 3 – (ii), 4 – (i)
(d) 1 – (iv), 2 – (ii), 3 – (i), 4 – (iii)
Answer:
(a) 1 – (ii), 2 – (iii), 3 – (i), 4 – (iv)

Question 36.
Time complexity of bubble sort in worst case is …………………………..
(a) θ(n)
(b) θ(n log n)
(c) θ(n2)
(d) θ(n(log n)2)
Answer:
(c) θ(n2)

Question 37.
The complexity of Merge Sort is …………………………
Answer:
o (n log n)

Question 38.
The complexity of Bubble Sort is …………………………
Answer:
o (n2)

Question 39.
The complexity of Binary search is ……………………….
Answer:
o (log n)

Question 40.
Pick the odd one out.
Merge Sort, Bubble, Binary, Insertion.
Answer:
Binary

PART – II
II. Answer The Following Questions

Question 1.
List the different factors in which the time efficiency of an algorithm its measured.
Answer:
The execution time that you measure in this case would depend on a number of factors such as:

• Speed of the machine
• Compiler and other system Software tools
• Operating System
• Programming language used
• The volume of data required

Question 2.
What is space – Time Tradeoff?
Answer:
A space-time of time-memory trade-off is a way of solving in less time by using more storage space or by solving a given algorithm in very little space by spending more time.

PART – III
III. Answer The Following Questions

Question 1.
Write a pseudo code for Binary Search
Answer:
1) Start with the middle element:
If the search element is equal to the middle element of the array
middle value = number of elements in array/2,
then return the index of the middle element.

• If not, then compare the middle element with the search value,
• If the search element is greater than the number in the middle index, then select the elements to the right side of the middle index, and go to Step-(l)
• If the search element is less than the number in the middle index, then select the elements to the left side of the middle index, and start with Step-(l)

2) When a match is found, display a success message with the index of the element matched.
3) If no match is found for all comparisons, then display an unsuccessful message

Question 2.
Differentiate Algorithm and Program?
Answer:
Algorithm:

1. The algorithm helps to solve a given problem logically and it can be contrasted with the program.
2. The algorithm can be categorized based on their implementation methods, design techniques, etc.
3. There is no specific rules for algorithm writing but some guidelines should be followed.
4. The algorithm resembles a pseudo-code which can be implemented in any language

Program:

1. Program is an expression of the algorithm in a programming language.
2. The algorithm can be implemented by a structured or object-oriented programming approach.
3. The program should be written for the selected language with specific syntax
4. Program is more specific o a programming language

Question 3.
What are the two phases in the Analysis of algorithms and performance evaluation?
Answer:
Analysis of algorithms and performance evaluation can be divided into two different phases:

• A Priori estimates: This is a theoretical performance analysis of an algorithm. The efficiency of an algorithm is measured by assuming the external factors.
• Posteriori testing: This is called performance measurement. In this analysis, actual statistics like running time and required for the algorithm executions are collected.

Question 4.
Write a pseudo code for Insertion sort
Answer:
Step 1 – If it is the first element, it is already sorted.
Step 2 – Pick the next element
Step 3 – Compare with all elements in the sorted sub-list
Step 4 – Shift all the elements in the sorted sub-list that is greater than the value to be sorted
Step 5 – Insert the value
Step 6 – Repeat until the list is sorted

Question 5.
Write note on Big \(\Theta\)?
Answer:
Big \(\Theta\)
When an algorithm has complexity with lower bound = upper bound, say that an algorithm has a complexity O (n log n) and Ω . (n log n), it actually has the complexity \(\Theta\) (n log n), which means the running time of that algorithm always falls in n log n in the best – case and worst – case.

PART – IV
IV. Answer The Following Questions

Question 1.
Explain Selection Sort?
Answer:
Selection sort
The selection sort is a simple sorting algorithm that improves the performance of bubble sort by making only one exchange for every pass through the list. This algorithm will first find the smallest elements in the array and swap it with the element in the first position of an array, then it will find the second smallest element and swap that element with the element in the second position, and it will continue until the entire array is sorted in respective order. This algorithm repeatedly selects the next-smallest element and swaps it into the right place for every pass. Hence it is called selection sort.

Pseudocode:
(I) Start from the first element (i.e.), index – 0, we search the smallest element in the array and replace it with the element in the first position.

(II) Now we move on to the second element position, and look for smallest element present in the sub-array, from starting index to till the last index of sub-array.

(III) Now replace the second smallest identified in step-2 at the second position in the or original array, or also called first position in the sub-array.

(IV) This is repeated until the array is completely sorted.
Let’s consider an array with values {13, 16, 11, 18, 14, 15}
Below, we have a pictorial representation of how selection sort will sort the given array

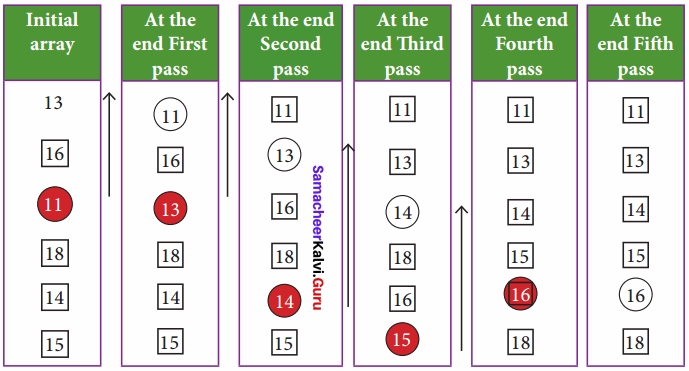
In the first pass, the smallest element will be 11, so it will be placed at the first position. After that, next smallest element will be searched from an array. Now we will get 13 as the smallest, so it will be then placed at the second position.

Then leaving the first element, next smallest element will be searched, from the remaining elements. We will get 13 as the smallest, so it will be then placed at the second position. Then leaving 11 and 13 because they are at the correct position, we will search for the next smallest element from the rest of the elements and put it at third position and keep doing this until array is sorted.
Finally we will get the sorted array end of the pass as shown above diagram.

Question 2.
Explain Insertion Sort?
Answer:
Insertion Sort
Insertion sort is a simple sorting algorithm. It works by taking elements from the list one by one and inserting them in their correct position into a new sorted list. This algorithm builds the final sorted array at the end. This algorithm uses an n-1 number of passes to get the final sorted list as per the previous algorithm as we have discussed.
Pseudo for Insertion sort
Step 1 – If it is the first element, it is already sorted.
Step 2 – Pick the next element
Step 3 – Compare with all elements in the sorted sub-list
Step 4 – Shift all the elements in the sorted sub-list that is greater than the value to be sorted
Step 5 – Insert the value
Step 6 – Repeat until list is sorted

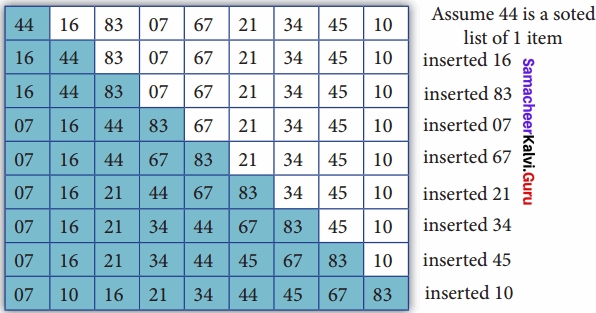
At the end of the pass the insertion sort algorithm gives the sorted output in ascending order as shown below: