Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

Exercise 1.1 Class 12 Maths State Board Question 1.
Find the adjoint of the following:

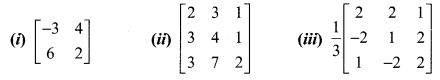
Solution:

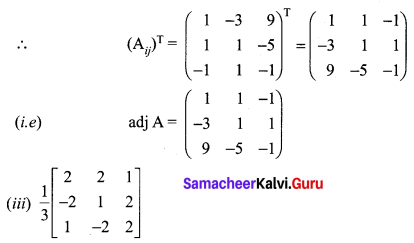
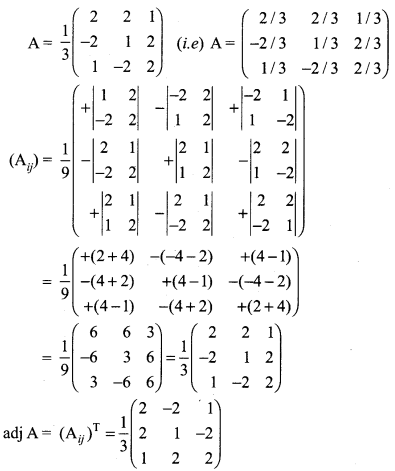
12th Maths Exercise 1.1 Answers Question 2.
Find the inverse (if it exists) of the following:

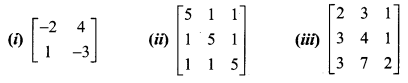
Solution:
For a matrix A, \(\mathrm{A}^{-1}=\frac{1}{|\mathrm{A}|}(\mathrm{adj} \mathrm{A})\). Where |A| ≠ 0. If |A| = 0 then A is called a singular matrix and so \(\mathrm{A}^{-1}\) does not exist.

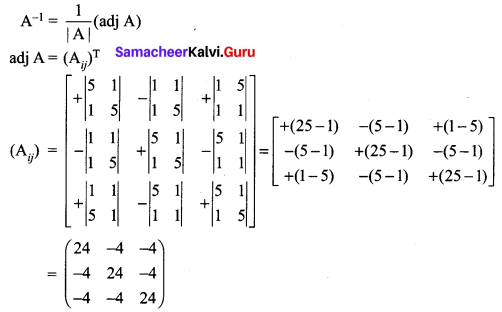
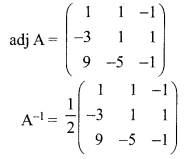
12th Maths Exercise 1.1 Question 3.
If F(α) = \(\left[\begin{array}{ccc}{\cos \alpha} & {0} & {\sin \alpha} \\ {0} & {1} & {0} \\ {-\sin \alpha} & {0} & {\cos \alpha}\end{array}\right]\) show that \([\mathrm{F}(\alpha)]^{-1}=\mathrm{F}(-\alpha)\)
Solution:
Let A = F (α)
So \([\mathrm{F}(\alpha)]^{-1}=\mathrm{A}^{-1}\)
Now

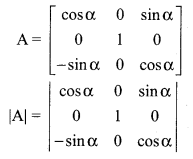
12th Maths Chapter 1 Exercise 1.1 Question 4.
If A = \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]\) show that A² – 3A – 7I₂ = O₂. Hence find A^-1.
Solution:
A = \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]\)

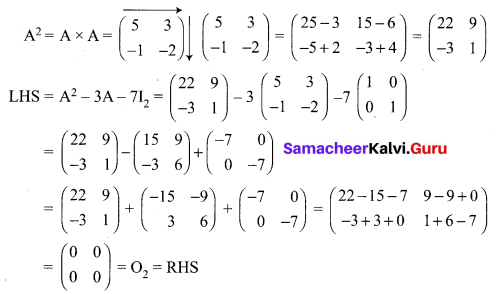
To Find A-1
Now we have proved that A² – 3A – 7I₂ = O₂
Post multiply by A^-1 we get
A – 3I – 7A^-1 = O₂

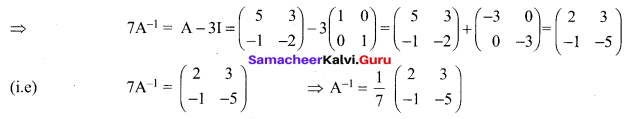
12th Maths Guide Pdf Free Download 2021 Question 5.
If \(\mathbf{A}=\frac{1}{9}\left[\begin{array}{ccc}{-8} & {1} & {4} \\ {4} & {4} & {7} \\ {1} & {-8} & {4}\end{array}\right]\) prove that A^-1 = A^T
Solution:

12th Maths Solution Book Pdf Download Question 6.
If \(\mathbf{A}=\left[\begin{array}{rr}{8} & {-4} \\ {-5} & {3}\end{array}\right]\), verify that A(adj A) = (adj A)A = |A| I₂
Solution:

Samacheer Kalvi 12 Maths Solutions Question 7.
If \(\mathbf{A}=\left[\begin{array}{ll}{3} & {2} \\ {7} & {5}\end{array}\right]\), and \(\mathbf{B}=\left[\begin{array}{cc}{-1} & {-3} \\ {5} & {2}\end{array}\right]\) verify that (AB)^-1 = B^-1 A^-1.
Solution:

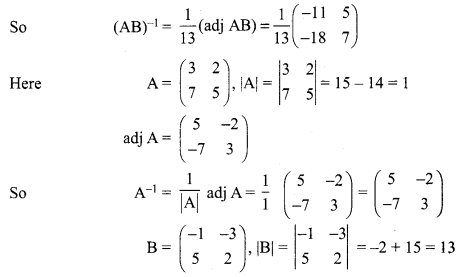
Samacheer Kalvi Guru 12th Maths Question 8.
If adj (A) = \(\left[\begin{array}{ccc}{2} & {-4} & {2} \\ {-3} & {12} & {-7} \\ {-2} & {0} & {2}\end{array}\right]\) find A
Solution:

12th Maths Guide Pdf Free Download Question 9.
If adj(A) = \(\left[\begin{array}{ccc}{0} & {-2} & {0} \\ {6} & {2} & {-6} \\ {-3} & {0} & {6}\end{array}\right]\) find A^-1
Solution:

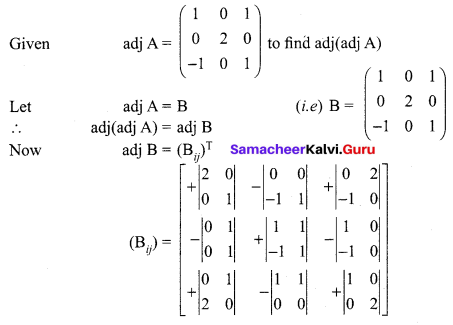
Samacheer Kalvi 12th Maths Guide Question 10.
Find adj(adj(A)) if adj A = \(\left[\begin{array}{ccc}{1} & {0} & {1} \\ {0} & {2} & {0} \\ {-1} & {0} & {1}\end{array}\right]\)
Solution:

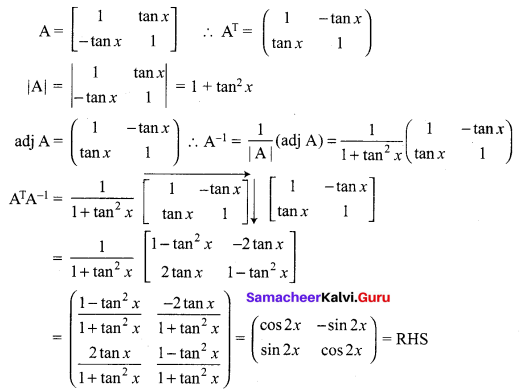
12th Samacheer Maths Solutions Question 11.

Solution:

12th Maths 1st Chapter Exercise 1.1 Question 12.
Find the matrix A for which A \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]=\left[\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right]\)
Solution:
Given A \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]=\left[\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right]\)
Let \(\mathrm{B}=\left(\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right) \text { and } \mathrm{C}=\left(\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right)\)
Given AB = C, To find A
Now AB = C
Post multiply by B^-1 on both sides
ABB^-1 = CB^-1 (i.e) A (BB^-1) = CB^-1
⇒ A(I) = CB^-1 (i.e) A = CB^-1
To find B^-1:

12th Maths Solution Book Question 13.
Given \(\mathbf{A}=\left[\begin{array}{cc}{1} & {-1} \\ {2} & {0}\end{array}\right], \mathbf{B}=\left[\begin{array}{cc}{3} & {-2} \\ {1} & {1}\end{array}\right] \text { and } \mathbf{C}\left[\begin{array}{ll}{1} & {1} \\ {2} & {2}\end{array}\right]\), find a matrix X such that AXB = C.
Solution:
A × B = C
Pre multiply by A^-1 and post multiply by B^-1 we get
A^-1 A × BB^-1 = A^-1CB^-1 (i.e) X = A^-1CB^-1

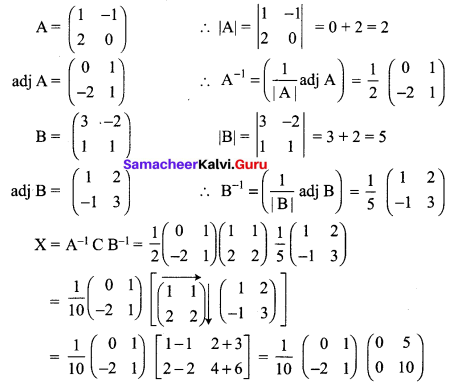
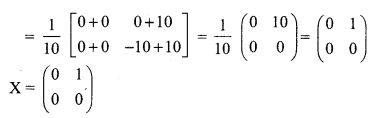
Maths Guide For Class 12 Question 14.

Solution:

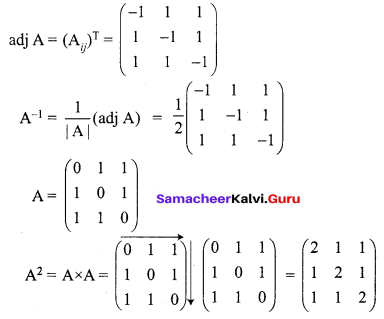
Maths 12th Guide Question 15.
Decrypt the received encoded message \(\left[\begin{array}{cc}{2} & {-3}\end{array}\right]\left[\begin{array}{ll}{20} & {4}\end{array}\right]\) with the encryption matrix \(\left[\begin{array}{cc}{-1} & {-1} \\ {2} & {1}\end{array}\right]\) and the decryption matrix as its inverse, where the system of codes are described by the numbers 1-26 to the letters A- Z respectively, and the number 0 to a blank space.
Solution:
Let the encoding matrix be \(\left[\begin{array}{cc}{-1} & {-1} \\ {2} & {1}\end{array}\right]\)


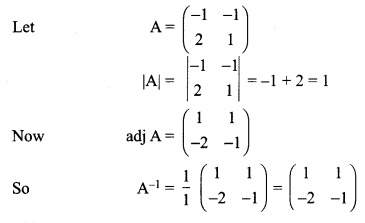
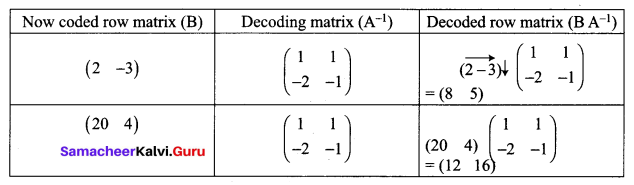
So the sequence of decoded matrices is [8 5], [12 16].
Thus the receivers read this message as HELP.

Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1 Additional Problems

12th Maths Solution Book Pdf Download English Medium 2021 Question 1.
Using elementary transformations find the inverse of the following matrix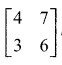
Solution:

12th Maths Solution Book Pdf Download English Medium Question 2.
Using elementary transformations find the inverse of the matrix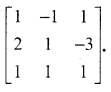
Solution:

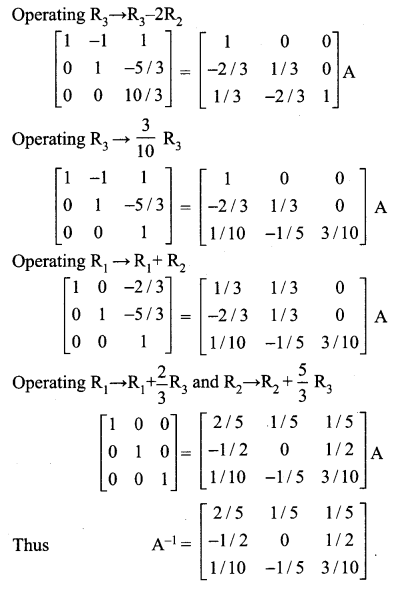
12th Maths Guide Samacheer Kalvi Question 3.
Using elementary transformation find the inverse of the matrix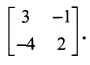
Solution:

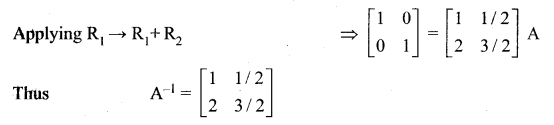
12th Maths Book Back Answers Question 4.
Using elementary transformations find the inverse of the matrix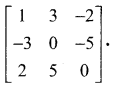
Solution:

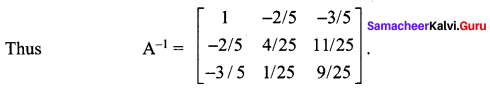
12th Maths Samacheer Solutions Question 5.
Using elementary transformation, find the inverse of the following matrix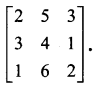
Solution:

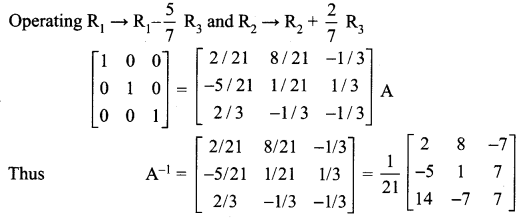
12th Samacheer Maths Solution Question 6.

Solution:

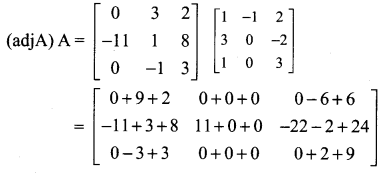
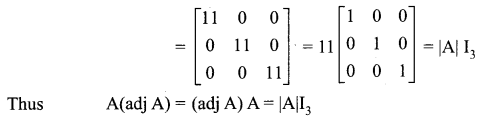
12th Maths Guide Pdf Download Question 7.

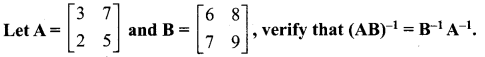
Solution:

12th Maths Book Back Questions With Answers Question 8.

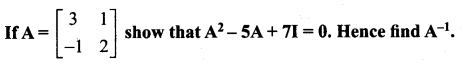
Solution:

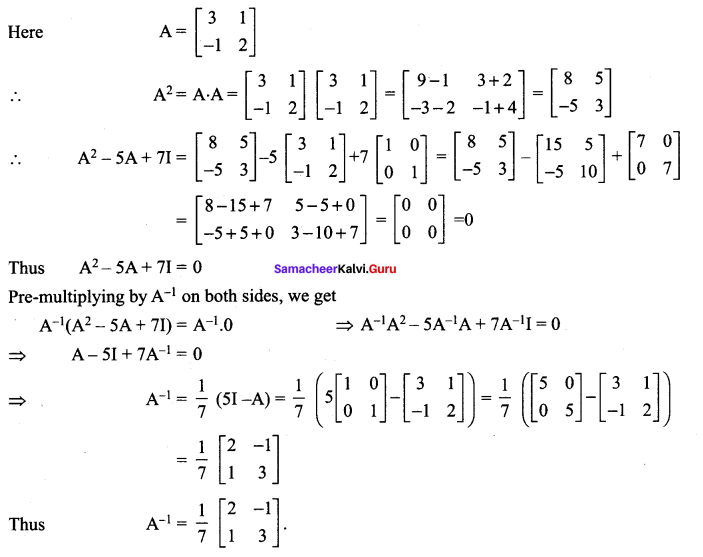
12th Samacheer Maths Guide Question 9.

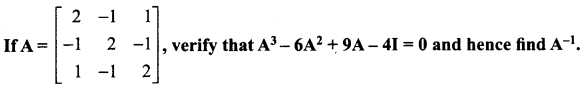
Solution:

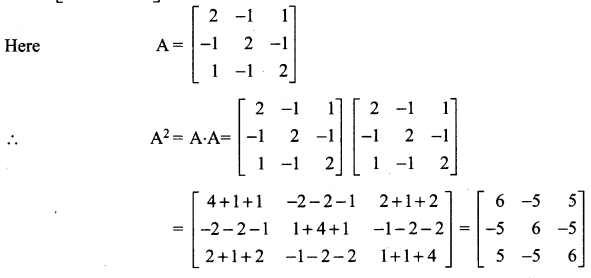
12th Maths Guide Free Download Question 10.

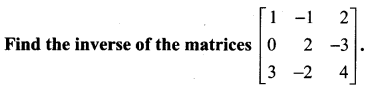
Solution: