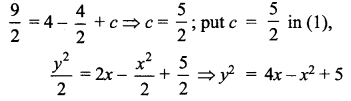Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.5

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Book Solutions Chapter 10 Ordinary Differential Equations Ex 10.5

Question 1.
If F is the constant force generated by the motor of an automobile of mass M, its velocity V is given by M\(\frac{d \mathbf{V}}{d t}\) = F – kV, where A is a constant. Express V in terms of t given that V = 0 when t = 0.
Solution:

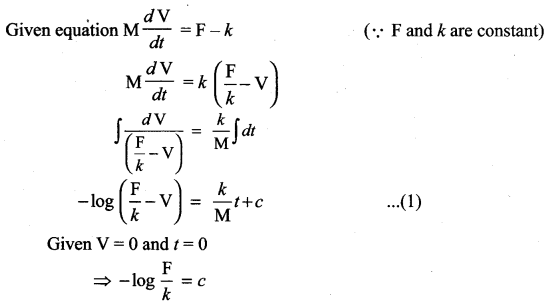
Substituting in (1)

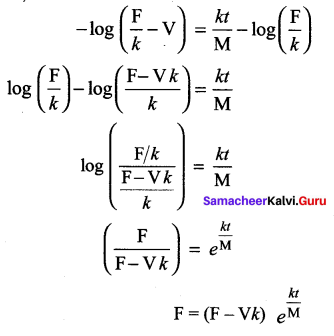
Question 2.
The velocity v, of a parachute falling vertically satisfies the equation, 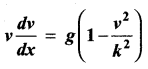where g and k are constants. If v and x are both initially zero, find v in terms of x.
Solution:


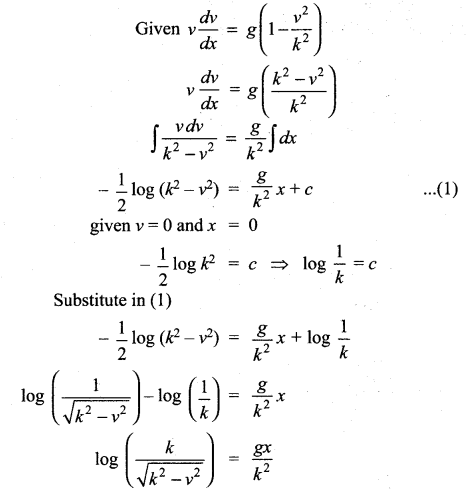
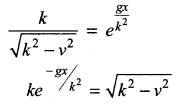
Squaring on both sides

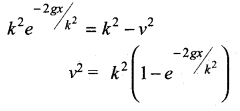
Question 3.
Find the equation of the curve whose slope is \(\frac{y-1}{x^{2}+x}\) and which passes through the point (1, 0).
Solution:


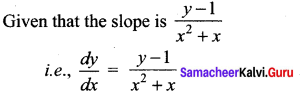
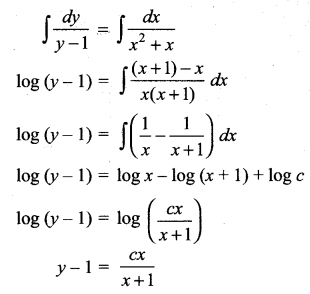
This passes through (1, 0)

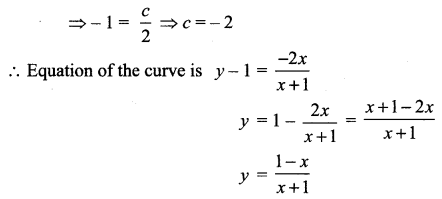
Question 4.
Solve the following differential equations:

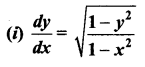
Solution:

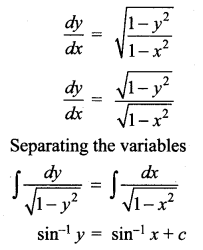
(ii) ydx + (1 + x²) tan^-1 x dy = 0
Solution:
ydx + (1 + x²) tan^-1 xdy = 0
(1 + x²) tan^-1x dy = -y dx
Separating the variables

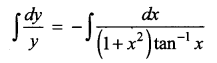
log y = – log (tan^-1 x) + log c
log y + log (tan^-1 x) = log c
log (y tan^-1 x) = log c
y tan^-1 x = c

(iii) sin \(\frac{d y}{d x}\) = a, y (0) = 1
Solution:

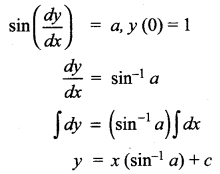
Given y(0) = 1
i.e., When x = 0, y = 1
∴ 1 = 0(sin^-1 a) + c ⇒ c = 1
∴ The solution is y = xsin^-1 a + 1

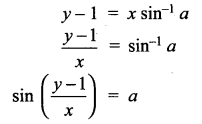
(iv)
Solution:

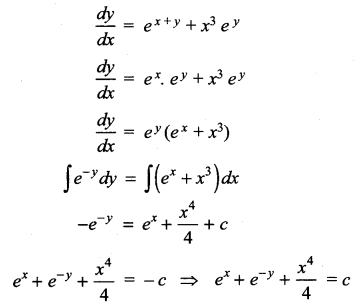
(v) (e^y + 1) cos x dx + e^y sin x dy = 0
Solution:
(e^y + 1) cos x dx + e^y sin x dy = 0
e^y sin x dy = – (e^y + 1) cos x dx

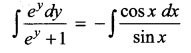
log (e^y + 1) = – log sin x + log c
log [(e^y + 1) + log sin x = log c
log (e^y +1) sin x] = log c
(e^y+ 1) sin x = c

(vi)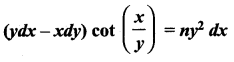
Solution:

(vii)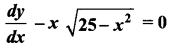
Solution:

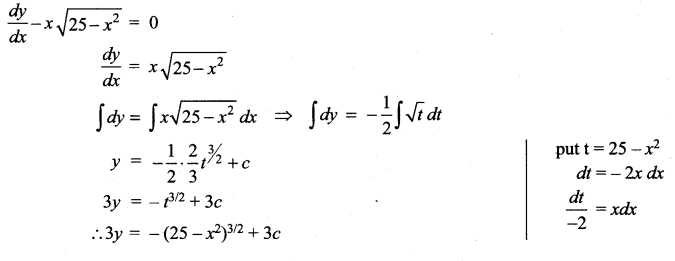
(viii) x cos y dy = e^x(x log x + 1)dx
Solution:

(ix)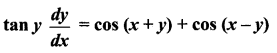
Solution:

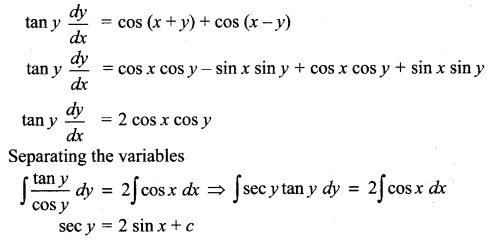
(x)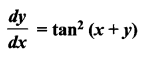
Solution:
\(\frac{d y}{d x}\) = tan² (x +y)
Let u = x + y
Differentiating with respect to ‘x’

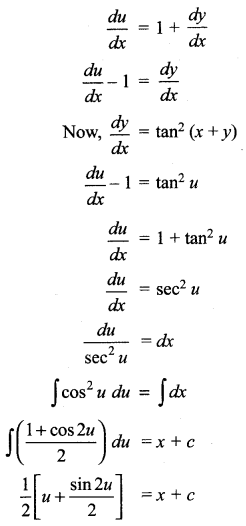
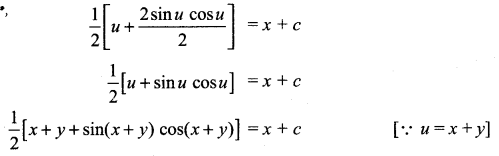
Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.5 Additional Problems

Question 1.

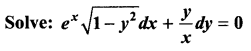
Solution:
The given equation can be written as

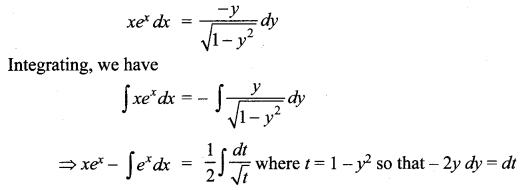
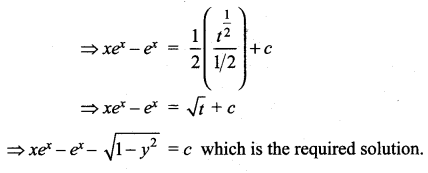
Question 2.

Solution:
Put x +y = z. Differentiating with respect to x we get

Question 3.
Find the cubic polynomial in x which attains its maximum value 4 and minimum value 0 at x = -1 and 1 respectively.
Solution:
Let the cubic polynomial bey = f(x). Since it attains a maximum atx = -1 and a minimum at x = 1.

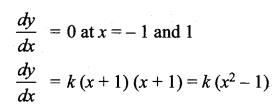
Separating the variables we have dy = k (x² – 1) dx


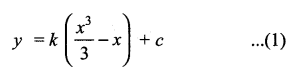
When x = – 1, y = 4 and when x =1,7 = 0
Substituting the equation (1) we have
2k + 3c = 12; – 2k + 3c =0
On solving we have k = 3 and c = 2. Substituting these values in (1) we get the required cubic polynomial y = x³ – 3x + 2.

Question 4.
The normal lines to a given curve at each point (x, y) on the curve pass through the point (2, 0). The curve passes through the point (2, 3). Formulate the differential equation representing the problem and hence find the equation of the curve.
Solution:
Slope of the normal at any point P(x, y) = \(-\frac{d x}{d y}\)

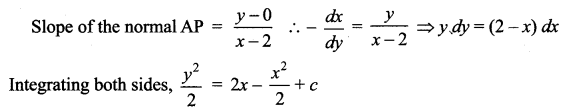
Since the curve passes through (2, 3)