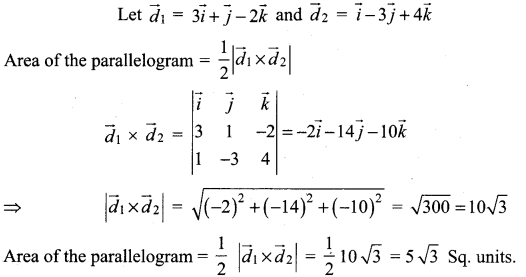You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.1
12th Maths 6th Chapter Solutions Question 1.
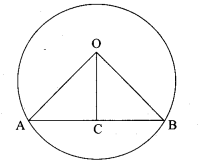
Prove by vector method that if a line is drawn from the centre of a circle of a circle to the midpoint of a chord, then the line is perpendicular to the chord.
Solution:
Let ‘C’ be the mid point of the chord AB
Take ‘O’ on the centre of the circle.
Since, OA = OB (Radii)
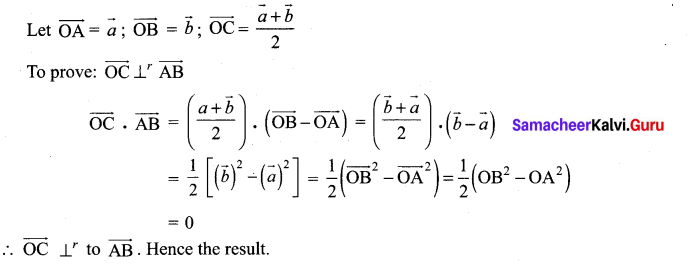
12th Maths Exercise 6.1 Question 2.
Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base.
Solution:
Let OAB be an isosceles triangle with OA = OB
Let OC be the median to the base AB
C is the midpoint of AB
Take O as origin.
12th Maths 6th Chapter Question 3.
Prove by vector method that an angle in a semi-circle is a right angle.
Solution:
Let AB be the diameter of the circle with centre ‘O’
Let P be any point on the semi-circle.
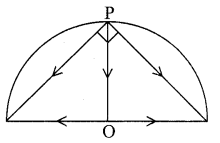
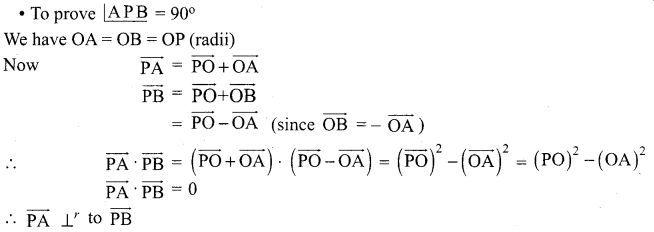
This gives ∠APB = 90°. Hence the result.
12th Maths Chapter 6 Exercise 6.1 Question 4.
Prove by vector method that the diagonals of a rhombus bisect each other at right angles.
Solution:
Let ABCD be a rhombus
Samacheer Kalvi Guru 12th Maths Question 5.
Using vector method, prove that if the diagonals of a parallelogram are equal, then it is a rectangle.
Solution:
Let ABCD be a parallelogram
To prove ABCD be a rectangle provided the diagonals are equal.
\(\overrightarrow{\mathrm{AB}}\) ⊥r to \(\overrightarrow{\mathrm{BC}}\)
⇒ ABCD is a rectangle.
Ex 6.1 Class 12 Question 6.
Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is \(\frac{1}{2}|\overrightarrow{\mathrm{AC}} \times \overrightarrow{\mathrm{BD}}|\)
Solution:
Vector area of quadrilateral ABCD = {Vector area of ∆ABC} + {Vector area of ∆ ACD}
6.1 12th Maths Question 7.
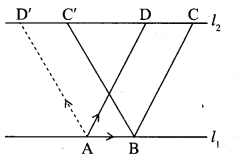
Prove by vector method that the parallelogram on the same base and between the same parallels are equal in area.
Solution:
Let ABCD and ABC’D’ be two parallelogram between the parallels with same base
To prove: Area of ABCD = Area of ABC’D’
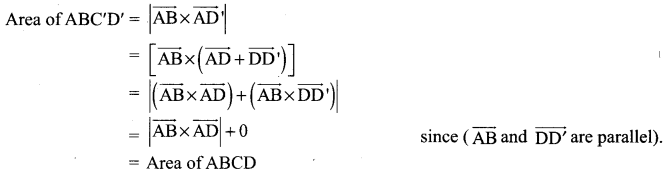
12th State Board Maths Solution Book Pdf English Medium Question 8.
If G is the centroid of a AABC, prove that.
(area of ∆GAB) = (area of ∆GBC) = (area of ∆GAC) = \(\frac{1}{3}\) [area of ∆ABC]
Solution:
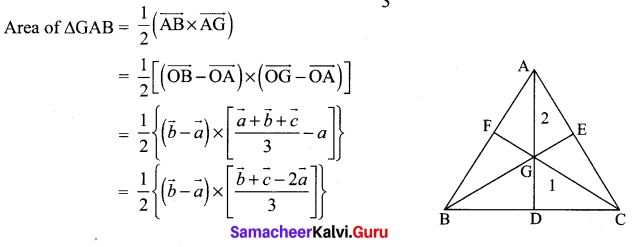
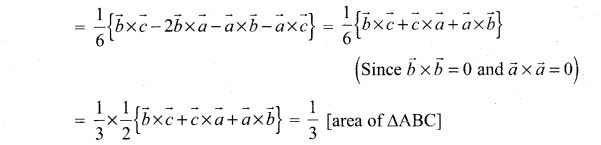
Similarly we can prove
Area of ∆GBC = Area of ∆GAC = \(\frac{1}{3}\) [Area of ∆ABC]
12th Maths Chapter 6 Solution Question 9.
Using vector method, prove that cos(α – β) = cos α cos β + sin α sin β.
Solution:
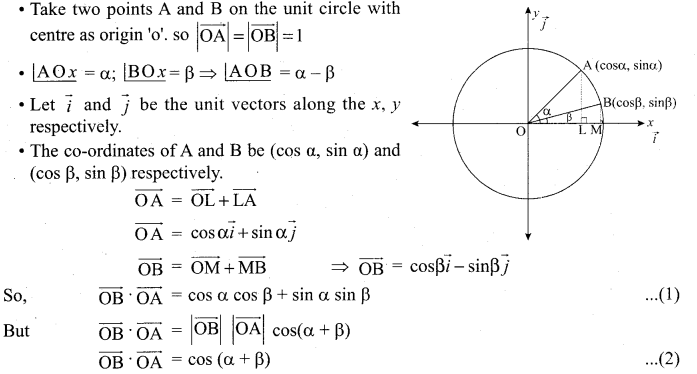
From (1) and (2), we get
cos(α + β) = cos α cos β + sin α sin β
Samacheer Kalvi 12 Maths Solutions Question 10.
Prove by vector method that sin(α + β) = sin α cos β + cos α sin β.
Solution:
Take two points A and B on the unit circle with centre as origin ‘O’, so \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|\) = 1
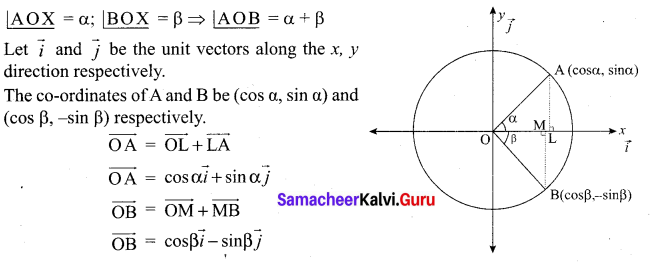
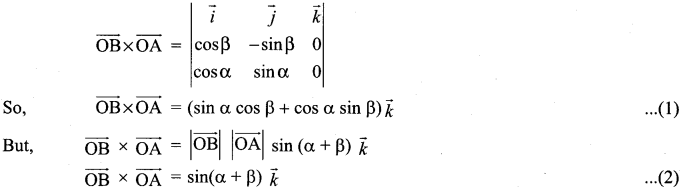
From (1) & (2), we get
sin (α + β) = sin α cos β + cos α sin β
12 Maths Samacheer Kalvi Solutions Question 11.
A particle acted on by constant forces \(8 \vec{i}+2 \vec{j}-6 \vec{k}\) and \(\overrightarrow{6 i}+2 \vec{j}-2 \vec{k}\) is displaced from the point (1, 2, 3) to the point (5, 4, 1). Find the total work done by the forces.
Solution:
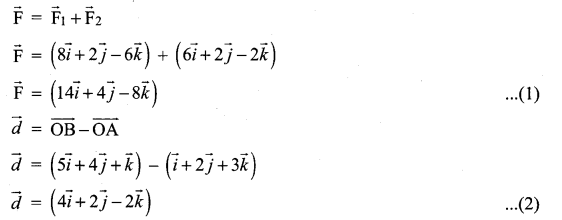
From (1) & (2), we get
Work done by the force = \(\overrightarrow{\mathrm{F}} \cdot \vec{d}\) = 56 + 8 + 16 = 80 units.
Std 12 Maths Solutions Samacheer Kalvi Question 12.
Forces of magnitude \(5 \sqrt{2}\) and \(10 \sqrt{2}\) units acting in the directions \((3 \vec{i}+4 \vec{j}+5 \vec{k})\) and \((10 \vec{i}+6 \vec{j}-8 \vec{k})\), respectively, act on a particle which is displaced from the point with position vector \((4 \vec{i}-3 \vec{j}-2 \vec{k})\) to the point with position vector \((\overrightarrow{6 i}+\vec{j}-3 \vec{k})\). Find the work done by the forces.
Solution:
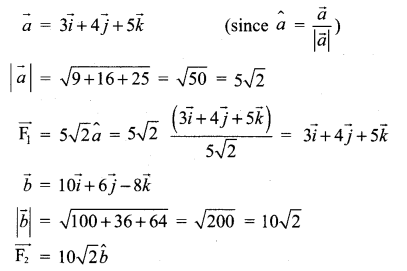
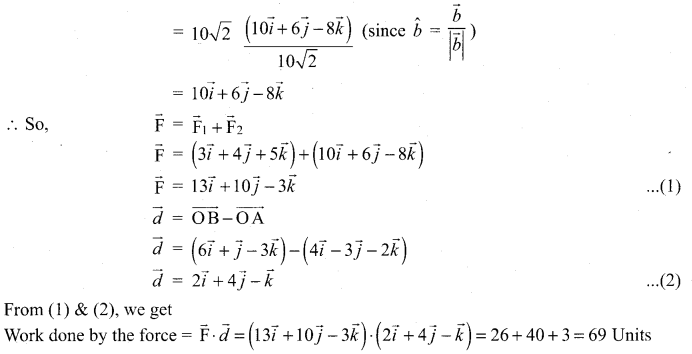
Class 12 Maths Solutions Samacheer Question 13.
Find the magnitude and direction cosines of the torque of a force represented by \(3 \vec{i}+4 \vec{j}-5 \vec{k}\) about the point with position vector \(2 \vec{i}-3 \vec{j}+4 \vec{k}\) acting through a point whose position vector is \(\overrightarrow{4 i}+2 \vec{j}-3 \vec{k}\).
Solution:
Samacheer Kalvi Guru 12 Maths Question 14.
Find the torque of the resultant of the three forces represented by \(-3 \vec{i}+6 \vec{j}-3 \vec{k}\), \(\overrightarrow{4 i}-10 \vec{j}+12 \vec{k}\) and \(\overrightarrow{4 i}+7 \vec{j}\) acting at the point with position vector \(8 \vec{i}-\overrightarrow{6} \vec{j}-4 \vec{k}\), about the point with position vector \(18 \vec{i}+3 \vec{j}-9 \vec{k}\)
Solution:
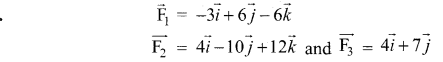
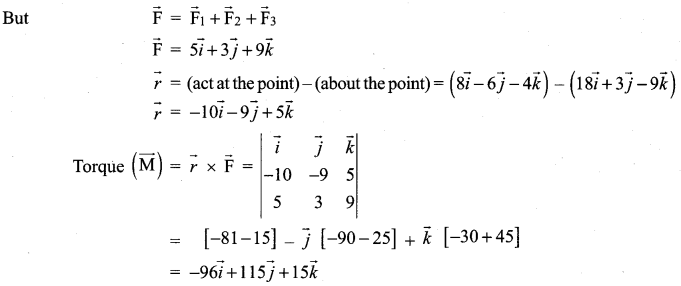
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.1 Additional Problems
Samacheer Kalvi Class 12 Maths Solutions Question 1.
The work done by the force \(\overrightarrow{\mathrm{F}}=a \vec{i}+\vec{j}+\vec{k}\) in moving the point of application from (1, 1, 1) to (2, 2, 2) along a straight line is given to be 5 units. Find the value of a.
Solution:
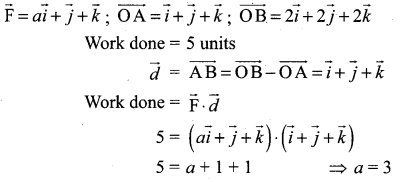
12 Maths Solutions Samacheer Kalvi Question 2.
If the position vectors of three points A, B and C are respectively 
and \(7(\vec{i}+\vec{k})\). Find \(\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}\). Interpret the result geometrically.
Solution:
Samacheer Kalvi.Guru 12th Maths Question 3.
A force given by and \(3 \vec{i}+2 \vec{j}-4 \vec{k}\) is applied at the point (1, – 1, 2). Find the moment of the force about the point (2, – 1, 3).
Solution:
Maths 12th Guide Question 4.
Show that the area of a parallelogram having diagonals 
is \(5 \sqrt{3}\)
Solution:
