Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Read More:

INDUSINDBK Pivot Point Calculator

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.6

Question 1.
Find the absolute extrema of the following functions on the given closed interval.
(i) f(x) = x³ – 12x + 10; [1, 2]
(ii) f(x) = 3x⁴ – 4x³ ; [-1, 2]

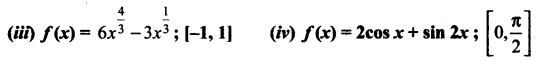
Solution:

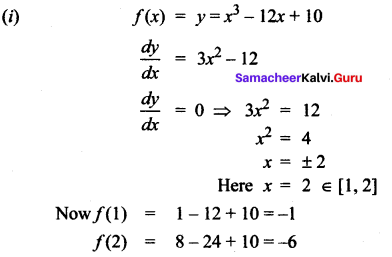
∴ Absolute maximum is – 1 and absolute minimum is – 6

(ii) f(x) = 3x⁴ – 4x³
f'(x) = 12x³ – 12x²
f'(x) = 0 ⇒ 12x²(x – 1) = 0
⇒ x = 0 or x = 1
[Here x = 0, 1 ∈ [-1, 2]]
Now f (-1) = 4
f(0) = 0
f(1) = -1
f(2) = 16
so absolute maximum = 16 and absolute minimum = -1

(iii)

(iv) f(x) = 2 cos x + sin 2x
f'(x) = -2 sin x + 2 cos 2x
f'(x) = 0 ⇒ cos 2x = sin x

Question 2.
Find the intervals of monotonicities and hence find the local extremum for the following functions

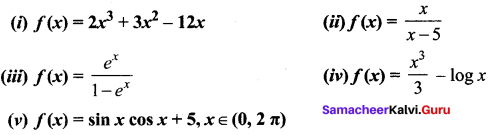
Solution:
(i) f(x) = 2x³ + 3x² – 12x
f'(x) = 6x² + 6x – 12
f'(x) = 0 ⇒ 6(x² + x – 2) = 0
(i.e.,) 6(x + 2)(x – 1) = 0
⇒ x = -2 or 1
Taking the points in the number line

The intervals are (-∞, -2), (-2, 1), (1, ∞)
when x ∈ (-∞, -2), f'(x) = 6 (-1) (-4) = +ve
say x = – 3
⇒ f(x) is strictly increasing in the interval (-∞, -2) when x ∈ (-2, 1), f’ (x) = 6 (2) (-1) = -ve
say x = 0
⇒ f(x) is strictly decreasing in the interval (-2, 1)
when x ∈ (1, ∞), f'(x) = 6 (4) (+1) = + ve say x = 2
⇒ f(x) is strictly increasing in (1, ∞)
Since f(x) changes from +ve to – ve when passing through -2, the first derivative, test tells us there is a local maximum at x = -2 and the local maximum value is f(-2) = 20.
Again f'(x) changes from – ve to +ve when passing through 1 ⇒ there is a local minimum at x = 1 and the local minimum value is f( 1) = -7. So (1 )f(x) is strictly increasing on (-∞, -2) and (1, ∞). And (2)f(x) is strictly decreasing on (-2, 1)
The local maximum = 20 and the local minimum = -7

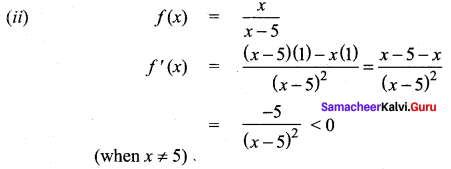
f(x) is strictly decreasing on (-∞, 5) and (5, ∞)
And there is no local extremum
(iii)

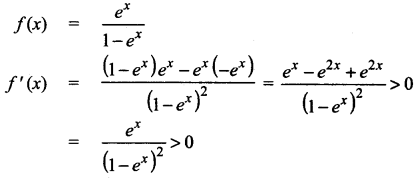
For all x values, so f(x) is strictly increasing in (-∞, ∞) and there is no local extremum.

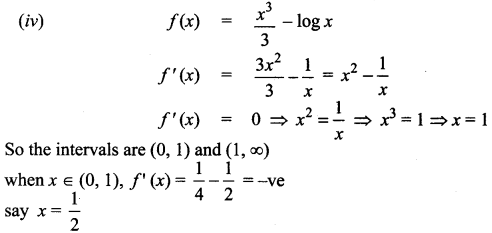
⇒ f(x) is strictly decreasing in (0, 1)

say x = 2
⇒ f(x) is strictly increasing in (1, ∞)
since f'(x) changes from -ve to +ve at x = 1, there is a local minimum at x = 1 and the local minimum values is f(1) = \(\frac{1}{3}-0=\frac{1}{3}\)
So the function is strictly decreasing on (0, 1) and strictly increasing on (1, ∞) and the local minimum value is \(\frac{1}{3}\)
(v)

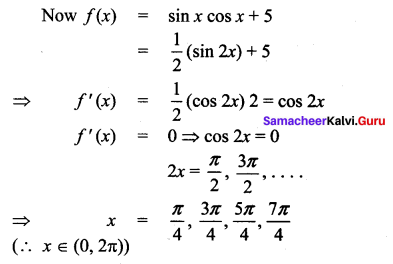
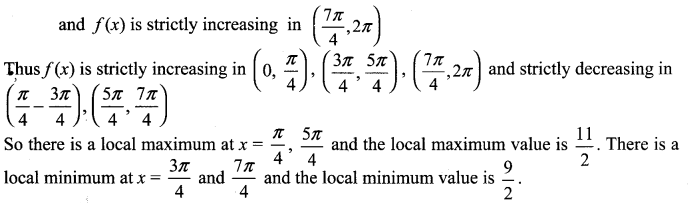
Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.6 Additional Problems

Find the absolute maximum and absolute minimum values of f on the given interval.

Question 1.
f(x) = 1 – 2x – x², [-4, 1]
Solution:
f(x) = 1 – 2x – x²
f'(x) = -2 – 2x
f'(x) = 0 ⇒ 2x = -2 ⇒ x = -1; The points are -4, -1, 1
At x = -4, f(x) = 1 – 2(-4) – (-4)² = 1 + 8 – 16 = -7
At x = -1, f(x) = 1 – 2 (-1) – (-1)² = 1 + 2 – 1 = 2
At x = 1, f(x) = 1 – 2 (1) – (1)² = 1 – 2 – 1 = – 2
Therefore, the absolute minimum is -7 and the absolute maximum is 2.

Question 2.
f(x) = x³ – 12x + 1, [-3, 5]
Solution:
f(x) = x³ – 12x + 1
f'(x) = 3x² – 12
f'(x) = 0 ⇒ 3x² – 12 = 0
3x² = 12 ⇒ x² = 4 ⇒ x = ±2
The x values are -3, -2, 2, 5
f(x) (at x = -3) = (-3)³ – 12 (-3) + 1 = -27 + 36 + 1 = 10
f(x) (at x = -2) = (-2)³ – (12)(-2) + 1 = -8 + 24 + 1 = 17
f(x) (at x = 2) = 2³ – 12 (2) + 1 = 8 – 24 + 1 = -15
f(x) (at x = 5) = 53 – 12 (5) + 1 = 125 – 60 + 1 = 66
From the above four values 10,17,-15 and 66, we see that absolute maximum is 66 and the absolute minimum is -15.

Question 3.

Solution:

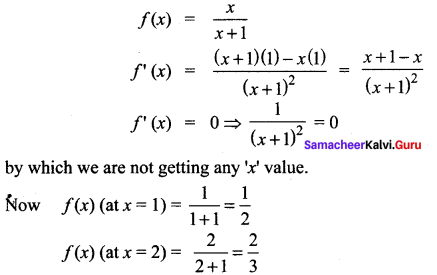
So, the absolute maximum is \(\frac{2}{3}\) and the absolute minimum is \(\frac{1}{2}\)

Question 4.
f(x) = sin x + cos x, [0, π/3]
f'(x) = sin x + cos x
f'(x) = cos x – sin x
f’ (x) = 0 ⇒ cos x – sin x = 0

Question 5.
f(x) = x – 2 cos x, [-π, π]
Solution:
f(x) = x – 2 cos x
f'(x) = 1 + 2 sin x
f'(x) = 0 ⇒ 1 + 2 sin x = 0

From the above values, absolute maximum is π + 2 and the absolute minimum is \(\frac{-\pi}{6}-\sqrt{3}\)

From the local maximum and minimum values of the following functions.

Question 6.
2x³ + 5 x² – 4x
Solution:

Local maximum = 12

Question 7.
t + cos t
Solution:

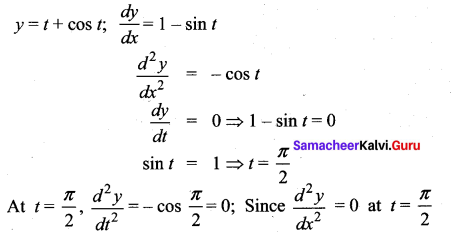
t = \(\frac{\pi}{2}\) is neither a maximum point nor a minimum point. So there is no maximum or minimum.