You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.8
Choose the correct or the most suitable answer from the given four alternatives.
Question 1.
A circular template has a radius of 10 cm. The measurement of radius has an approximate error of 0.02 cm. Then the percentage error in calculating area of this template is …….
(a) 0.2%
(b) 0.4%
(c) 0.04%
(d) 0.08%
Solution:
(b) 0.4%
Hint:
r = 10 cm
dr = 0.02
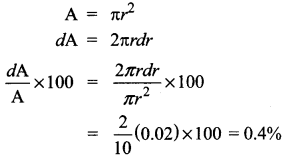
Question 2.
The percentage error of fifth root of 31 is approximately how many times the percentage error in 31?

Solution:
\(\frac{1}{5}\)
Hint:
We know that the percentage error in the «th root of a number is approximately \(\frac{1}{n}\) times the percentage error in the number.
![]()
![]()
Question 3.
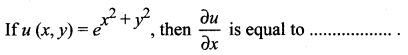
![]()
Solution:
(b) 2xu
Hint:
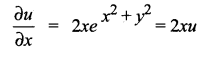
Question 4.
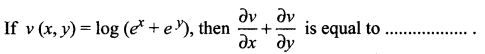
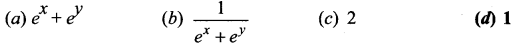
Solution:
(d) 1
Hint:
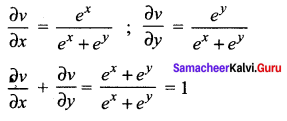
![]()
Question 5.
If w (x, y) = xy, x > 0, then \(\frac{\partial w}{\partial x}\) is equal to ……
![]()
Solution:
(c) yxy – 1
Hint:
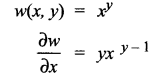
Question 6.
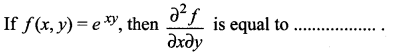
(a) xyexy
(b) (1 + xy)exy
(c) (1 + y)exy
(d) (1 + x)exy
Solution:
(b) (1 + xy)exy
Hint:

Question 7.
If we measure the side of a cube to be 4 cm with an error of 0.1 cm, then the error in our calculation of the volume is …….
(a) 0.4 cu.cm
(b) 0.45 cu.cm
(c) 2 cu.cm
(d) 4.8 cu.cm
Solution:
(d) 4.8 cu.cm
Hint.
a = 4 cm
da = 0.1 cm
v = a3
dv = 3a2da
= 3(4)2 (0.1)
= 4.8 cu. cm
![]()
Question 8.
The change in the surface area S = 6x2 of a cube when the edge length varies from x0 to x0 + dx is …….
(a) 12x0 + dx
(b) 12x0dx
(c) 6x0dx
(d) 6x0 + dx
Solution:
(b) 12x0dx
Question 9.
the approximate change in the volume: V of a cube of side x mentres caused by increasing the side by 1% is ……..
(a) 0.3 xdx m3
(b) 0.03 x m3
(c) 0.03 x2 m3
(d) 0.03 x3m3
Solution:
(d) 0.03 x3m3
Hint:
Let the side of the cube be x units
v = x3
when dx = 0.01x
dv = 3x2dx
= 3x2(0.01 x)
= 0.03 x3m3
Question 10.
If g(x, y) = 3x2 – 5y + 2y2, x(t) = et and y(t) = cos t, then \(\frac{d g}{d t}\) is equal to ……..
(a) 6e2t + 5 sin t – 4 cos t sin t
(b) 6e2t – 5 sin t + 4 cos t sin t
(c) 3e2t + 5 sin t + 4 cos t sin t
(d) 3e2t – 5 sin t + 4 cos t sin t
Solution:
(a) 6e2t + 5 sin t – 4 cos t sin t
Question 11.
![]()
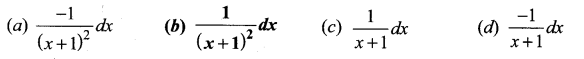
Solution:
(b) \(\frac{1}{(x+1)^{2}} d x\)
Hint:
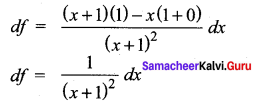
Question 12.
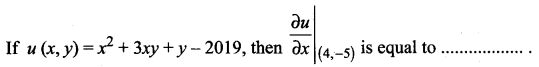
(a) -4
(b) -3
(c) -7
(d) 13
Solution:
(c) -7
Hint:
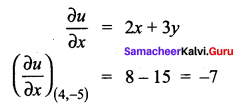
![]()
Question 13.
![]()

Solution:
(b) \(-x+\frac{\pi}{2}\)
Hint:

Question 14.
If w(x, y, z) = x2 (y – z) + y2 (z – x) + z2 (x – y), then 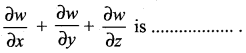
(a) xy + yz + zx
(a) xy + yz + zx
(b) x(y + z)
(c) y(z + x)
(d) 0
Solution:
(d) 0
Hint:

Question 15.
If f(x, y, z) = xy + yz + zx, then fx – fz is equal to ……….
(a) z – x
(b) y – z
(c) x – z
(d) y – x
Solution:
(a) z – x
Hint:
fx = y + z
fz = y + x
fx – fz = y + z – y – x = z – x
Additional Problems
Question 1.
If u = xy then is equal to ……..
(a) yxy – 1
(b) u log x
(c) u log y
(d) xyx – 1
Solution:
(a) yxy – 1
Hint:
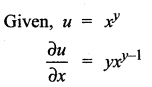
![]()
Question 2.
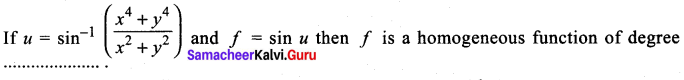
(a) 0
(b) 1
(c) 2
(d) 4
Solution:
(c) 2
Hint:

Question 3.
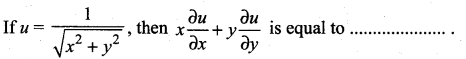

Solution:
(d) -u
Hint:

Question 4.
The curve y2 (x- 2) = x2 (1 +x) has …….
(a) an asymptote parallel to x-axis
(b) an asymptote parallel to y-axis
(c) asymptotes parallel to both axis
(d) no asymptotes
Solution:
(b) an asymptote parallel to y-axis
Hint:
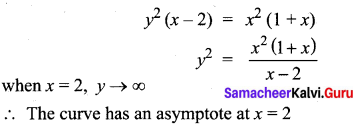
![]()
Question 5.
If x = r cos θ, y = r sin θ, then \(\frac{\partial r}{\partial x}\) is equal to …….
(a) sec θ
(b) sin θ
(c) cos θ
(d) cosec θ
Solution:
(c) cos θ
Hint:
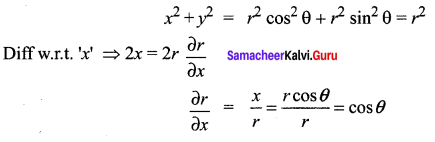
Question 6.
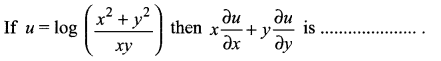
(a) 0
(b) u
(c) 2u
(d) u – 1
Solution:
(a) 0
Hint:

Question 7.
The percentage error in the 11th root of the number 28 is approximately …. times the precentage error is 28.

Solution:
\(\frac{1}{11}\)
Hint:
![]()
Take log on both sides

The percentage error is approximately \(\frac{1}{11}\) times the percentage error is 28.
Question 8.
The curve a2y2 = x2 (a2 – x2) has ……
(a) only one loop between x = 0 and x = a
(b) two loops between x = 0 and x = a
(c) two loops between x = – a and x = a
(d) no loop
Solution:
(c) two loops between x = – a and x = a
Hint.
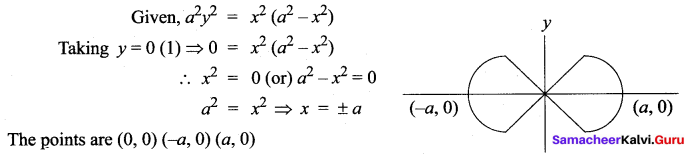
Question 9.
An asymptote to the curve y2 (a + 2x) = x2 (3a – x) is ………
(a) x = 3a
(b) x = – a/2
(c) x = a/2
(d) x = 0
Solution:
(b) x = – a/2
Hint.
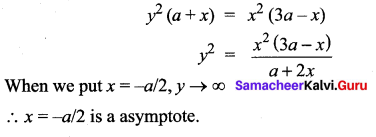
![]()
Question 10.
In which region the curve y2 (a + x) = x2 (3a – x) does not lie?
(a) x > 0
(b) 0 < x < 3a (c) x ≤ – a and x > 3a
(d) – a < x < 3a Solution: (c) x ≤ – a and x > 3a
Hint.
y2 (a + x) = x2 (3a – x)
Taking y = 0 (1) ⇒ 0 = x2 (3a – x)
= x = 0, x = 3a
∴ The points are (0, 0) (3a, 0)
There is a loop between x = 0 and x = 3a
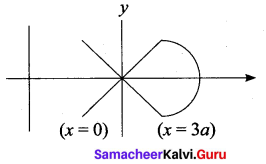
when x > 3 a, y ➝ imaginary
the curves does not exist beyond x = 3a i.e., x > 3a
the curve has asymptote at x = -a
the curve does not exist when x < -a
the curve exists in the region – a < x < 3a
Question 11.
If M = y sin x, then \(\frac{\partial^{2} u}{\partial x \partial y}\) is equal to …….
(a) cos x
(b) cos y
(c) sin x
(d) 0
Solution:
(a) cos x
Hint:
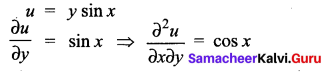
Question 12.
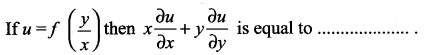
(a) 0
(b) 1
(c) 2u
(d) u
Solution:
(a) 0
Hint:
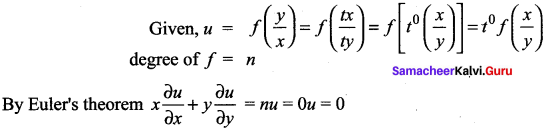
Question 13.
The curve 9y2 = x2 (4 – x2) is symmetrical about …….
(a) y – axis
(b) x – axis
(c) y = x
(d) both the axes
Solution:
(d) both the axes
Hint.
Replace x by – x and y by -y
9 (-y2) = (-x)2(4-(-x)2)
The equation is unaltered
∴ the curve is symmetrical about both the axes.
![]()
Question 14.
The curve ay2 = x2 (3a – x) cuts the y – axis at …….
(a) x = – 3a, x = 0
(b) x = 0, x = 3a
(c) x = 0, x = a
(d) x = 0
Solution:
(d) x = 0
Hint:
Given ay2 = x2 (3a – x)
The point of intersection with y-axis by putting x = O
In (1) = ay2 = 0 (3a – 0)
ay = 0 ; y = 0
∴ The curve intersects y-axis at the origin is x = 0