Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 1 Chapter 4 நேர் மற்றும் எதிர் விகிதங்கள் Ex 4.3 Textbook Questions and Answers, Notes.
TN Board 7th Maths Solutions Term 1 Chapter 4 நேர் மற்றும் எதிர் விகிதங்கள் Ex 4.3
பல்வகைத் திறனறி பயிற்சிக் கணக்குகள்
Question 1.
7கி.கி வெங்காயத்தின் விலை 384 எனில் பின்வருவனவற்றைக் காண்க
(i) ₹ 180 இக்கு வாங்கிய வெங்காயத்தின் எடை
(ii) 3 கி.கி வெங்காயத்தின் விலை
தீர்வு :
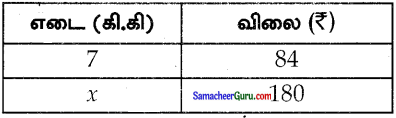
\(\frac{7}{x}=\frac{84}{180}\)
x × 84 = 7 × 180
x = \(\frac{7 \times 180}{84}\)
x = 15 கி.கி
(ii) தீர்வு :
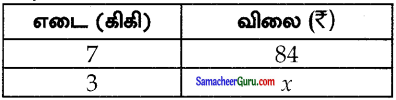
எடை அதிகரிக்க விலையும் அதிகரிக்கும்
\(\frac{7}{3}=\frac{84}{x}\)
74 × x = 84 × 3
x = \(\frac{84 \times 3}{7}\)
x =₹36
![]()
Question 2.
C = kd, என்பதில்
i) C இக்கும் d இக்கும் இடையேயுள்ள ப உறவு என்ன?
ii) C = 30 மற்றும் d = 6 எனில் k ன் – மதிப்பு என்ன?
iii) d = 10 எனில், என் மதிப்பு என்ன ?
தீர்வு:
i) நேர் விகிதம்
ii) c = kd
k = \(\frac{c}{d}=\frac{30}{6}\)
k = 5
iii) c = kd
= 5 × 10
c = 50
பத்து போட்டது
Question 3.
தமிழ்ச்செல்வன் ₹ 5000 ஐ மூன்று மாதத்திற்கு ஒரு முறை வங்கிக்கணக்கில் சேமித்து வருகிறார். அவர் ₹1,50,000 ஐ சேமிக்க எத்தனை வருடங்களாகும்.
தீர்வு :
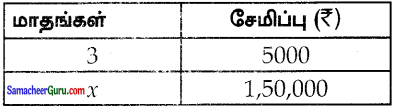
சேமிப்பு அதிகரிக்க சேமிக்கும் மாதமும் அதிகரிக்கிறது
\(\frac{3}{x}=\frac{5000}{150000}\)5000 × x = 3 × 15,000
x = \(\frac{3 \times 150000}{5000}\)
x = 90 மாதங்கள்
![]()
Question 4.
ஓர் அச்சு இயந்திரம் 300 பக்கங்களைக் கொண்ட… ஒரு புத்தகத்தை 1 நிமிடத்தில் 30 பக்கங்கள் என அச்சிடுகிறது. அவ்வச்சு இயந்திரம் அதே புத்தகத்தை 1 நிமிடத்தில் 25 பக்கங்கள் என அச்சிட்டால், அச்சிட்டு முடிக்க எத்தனை நிமிடங்கள் ஆகும்?
தீர்வு:
புத்தகத்திலுள்ள பக்கங்களின் எண்ணிக்கை = 300
1 நிமிடத்தில் அச்சிட ஆகும் பக்கங்கள் = 30
அச்சிட ஆகும் நேரம் = \(\frac{300}{30}\) = 10 நிமிடங்கள்
அதே புத்தகத்தை அச்சிட்டு முடிக்க ஆகும் நேரம் = \(\frac{300}{25}\) = 12 நிமிடங்கள்
Question 5.
6 பழரசப் பாட்டில்களின் விலை ₹ 210, எனில் 4 பழரசப் பாட்டில்களின் விலை என்ன?
தீர்வு:

பாட்டில்களின் எண்ணிக்கை குறைய விலையும் குறையும்
\(\frac{6}{4}=\frac{210}{x}\)
6 × x = 210 × 4
x = \(\frac{210 \times 4}{6}\)
x = ₹ 1140
Question 6.
X ஆனது yன் இருமடங்கோடு எதிர்விகிதத் தொடர்புடையது. கொடுத்துள்ளபடி y = 6, எனில் ன் மதிப்பு 4 y = 8 எனில் x ன் மதிப்பைக் காண்க.
தீர்வு:
x ∝ \(\frac{1}{2 \mathrm{y}}\)
x = \(\frac{\mathrm{k}}{2 \mathrm{y}}\) (k மாறிலி))
y = 6 எனில் x = 4
⇒ 4 = \(\frac{\mathrm{k}}{12}\)
⇒ k = 4 x 12 = 48
y = 8 எனில் x = \(\frac{48}{2 \times 8}=\frac{48}{16}\) ⇒ 3
x = 3
![]()
Question 7.
ஒரு சரக்கு வண்டி 594 கி.மீ தூரத்தை கடக்க 108 லி டீசல் தேவைப்படுகிறது எனில் அவ்வண்டி 1650 கி.மீ தூரத்தைக் கடக்கத் தேவைப்படும் டீசலின் அளவு எவ்வளவு?
தீர்வு :
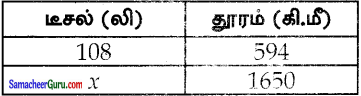
தூரம் அதிகரிக்க டீசலின் அளவும் அதிகரிக்கும்
\(\frac{108}{x}=\frac{594}{1650}\)x × 594 = 108 × 1650
\(\frac{108}{x}=\frac{594}{1650}\)
x = 300 லிட்டர்
மேற்சிந்தனைக் கணக்குகள்
Question 8.
ஒரு டசன் (dozen) சோப்புகளின் விலை ₹396, எனில், 35 சோப்புகளின் விலை என்ன?
தீர்வு :

எண்ணிக்கை அதிகரிக்க விலையும் அதிகரிக்கும்
\(\frac{12}{35}=\frac{396}{x}\)
12 × x = 396 × 35
x = \(\frac{396 \times 35}{12}\)
x = ₹ 1155
![]()
Question 9.
ஒரு பள்ளியில் 45 நிமிடங்களைக் கொண்ட 7 பாட வேளைகள் உள்ளன. அப்பள்ளியில் பாட வேளைகள் 9 ஆக மாறும்போது ஒவ்வொரு பாட வேளையின் கால அளவு எவ்வளவு?
தீர்வு :
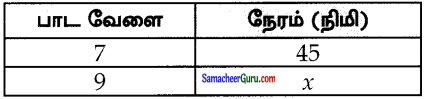
பாடவேளை அதிகரிக்க நேரம் குறையும்
9 × x = 7 × 45
x = \(\frac{7 \times 45}{9}\)
x = 35 நிமி
Question 10.
105 நோட்டுப் புத்தகங்களின் விலை ₹ 2415. ₹ 1863 இக்கு எத்தனை நோட்டுப் புத்தகங்கள் வாங்கலாம்?
தீர்வு :

விலை குறைய எண்ணிக்கையும் குறையும் 105 2415
\(\frac{105}{x}=\frac{2415}{1863}\)
x × 2415 = 105 × 1863
x = \(\frac{105 \times 1863}{2415}\) ⇒ 81 புத்தகங்கள்
![]()
Question 11.
10 விவசாயிகள் 21 நாட்களில் நிலத்தை உழுது முடிக்கின்றனர் எனில், அதே நிலத்தை 14 விவசாயிகள் எத்தனை நாள்களில் உழுது முடிப்பர்?
தீர்வு :
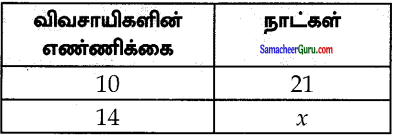
எண்ணிக்கை அதிகரிக்க நாட்கள் குறையும்
14 × x = 10 × 21
x = \(\frac{10 \times 21}{14}\)
x = 15 நாட்கள்
Question 12.
ஒரு வெள்ள நிவாரண முகாமில் 80 நபர்களுக்குத் தேவையான உணவு 60 நாள்களுக்குப் போதுமானதாக உள்ளது. 10 நாள்களுக்குப் பின்னர், 20 நபர்கள் அந்த முகாமில் வந்து சேர்ந்தார்கள் எனில், அவ்வுணவு எத்தனை நாள்களுக்குப் போதுமானதாக இருக்கும்?
தீர்வு :
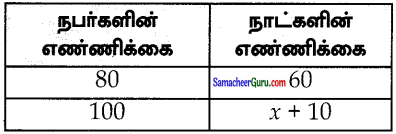
நபர்களின் நாட்களின் எண்ணிக்கை எண்ணிக்கை
\(\frac{80}{100}=\frac{60}{x+10}\)80(x + 10) = 60 × 100
x + 10 = \(\frac{60 \times 100}{80}\)
x + 10 = 75
x = 75 – 10 = 65
நாட்கள் = 65 – 60 = 5 நாட்கள்
![]()
Question 13.
6 நபர்கள் ஒரு வேலையை 12 நாள்களில் செய்து முடிக்கின்றனர். 2 நாள்கள் கழித்து மேலும் 6 நபர்கள் வந்து சேர்கிறார்கள் எனில், அவ்வேலையைச் செய்ய எத்தனை நாள்கள் எடுத்துகொள்வார்கள்?
தீர்வு :
ஒரு நாளில் செய்யும் வேலையை y என்க. மொத்த வேலை = 6 × 12 × y = 72y
2 நாள்கள் கழித்து மேலும் 6 நபர்கள் செய்யும் வேலை = 6 × 2xy = 12y
மீதமுள்ள வேலை = 72y – 12 y = 60y
மொத்த நபர்கள் = 6 + 6 = 12
ஒரு நாளைக்கு செய்யும் வேலை = 12y

= \(\frac{60 y}{12 y}\) = 5 நாட்கள்