Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.5
Question 1.
One night in Kashmir, the temperature is -5°C. Next day the temperature is 9°C. What is the increase in temperature?
Solution:
Temperature in the first day = -5°C
Temperature in the next day = 9°C
∴ Increase in temperature = 9°C – (-5°C)
= 9°C + (+5°C) = 14°C
Question 2.
An atom can contain protons which have a positive charge (+) and electrons which have a negative charge (-). When an electron and a proton pair up, they become neutral (0) and cancel the charge at. Now determine the net charge:
(i) 5 electrons and 3 protons → -5 + 3 = -2 that is 2 electrons \(\ominus\ominus\)
(ii) 6 protons and 6 electrons →
(iii) 9 protons and 12 electrons →
(iv) 4 protons and 8 electrons →
(v) 7 protons and 6 electrons →
Solution:
(ii) 6 protons and 6 electrons → (+6) + (-6) = 0
(iii) 9 protons and 12 electrons → (+9) + (-12) = 9-12 = -3 ⇒ 3 electrons \(\ominus\ominus\ominus\)
(iv) 4 protons and 8 electrons → (+4) + (-8) = +4 – 8 = -4 ⇒ 4 electrons \(\ominus\ominus \ominus\ominus\)
(v) 7 protons and 6 electrons → (+7) + (-6) = +1 = 1 proton \(\oplus\)
Question 3.
Scientists use the Kelvin scale (K) as an alternative temperature scale to degrees Celsius (°C) by the relation T°C = (T + 273)K. Convert the following to Kelvin:
(i) -275°C
(ii) 45°C
(iii) -400°C
(iv) -273°C
Solution:
(i) -275°C = (-275 + 273)K = -2K
(ii) 45°C = (45 + 273)K = 318 K
(iii) -400°C = (-400 + 273)K = -127 K
(iv) -273°C = (-273 + 273) K = 0K
![]()
Question 4.
Find the amount that is left in the student’s bank account, if he has made the following transaction in a month. His initial balance is ₹ 690.
(i) Deposit (+) of ₹ 485
(ii) Withdrawal (-) of ₹ 500
(iii) Withdrawal (-) of ₹ 350
(iv) Deposit (+) of ₹ 89
(v) If another ₹ 300 was withdrawn, what would the balance be?
Solution:
(i) Initial balance of student’s account = ₹ 690
Deposited amount = ₹ 485 (+)
∴ Amount left in the account = ₹ 690 + ₹ 485 = ₹ 1175
(ii) Balance in the account = ₹ 1175
Amount withdrawn = ₹ 500 (-)
Amount left = ₹ 1175 – ₹ 500 = ₹ 675
(iii) Balance in the account = ₹ 675
Amount withdrawn = ₹ 350 (-)
Amount left = ₹ 675 – ₹ 350 = ₹ 325
(iv) Balance in the account = ₹ 325
Amount deposited = ₹ 89(+)
Amount left = ₹ 325 + ₹ 89 = ₹ 414
(v) Balance in the account = ₹ 414
Amount withdrawn = ₹ 300 (-)
Amount left = ₹ 414 – ₹ 300 = ₹ 114
Question 5.
A poet Tamizh Nambi lost 35 pages of his ‘lyrics’ when his file had got wet in the rain. Use integers, to determine the following.
(i) If Tamil Nambi wrote 5 pages per day, how many day’s work did he lose?
(ii) If four pages contained 1800 characters, (letters) how many characters were lost?
(iii) If Tamil Nambi is paid ₹ 250 for each page produced, how much money did he lose?
(iv) If Kavimaan helps Tamizh Nambi and they are able to produce 7 pages per day, how many days will it take to recreate the work lost?
(v) Tamizh Nambi pays Kavimann ₹ 100 per page for his help. How much money does Kavimaan receive?
Solution:
Total pages lost – 35
One day work = 5 page 35
35 pages = \(\frac{35}{5}\) = 7 days work
∴ 7 day’s work he lost.
(ii) Number of characters in four pages = 1800
Number of characters in one page = \(\frac{1800}{4}\) = 450
∴ Number of characters in 35 pages = 450 × 35 = 15,750 characters
(iii) Payment for one page = ₹ 250
∴ Payment for 35 pages = ₹ 250 × ₹ 35 = ₹ 8,750
(iv) Number of pages recreated a day = 7
∴ To recreate 35 pages day’s needed = \(\frac{35}{7}\) = 5 days
(v) Payment of Kavimaan = ₹ 100 per page
∴ for 35 pages payment = ₹ 100 × 35 = ₹ 3,500
Question 6.
Add 2 to me. Then multiply by 5 and subtract 10 and divide new by 4 and I will give you 15! Who am I?
Solution:
According to the problem {[(I + 2) × 5] – 10} ÷ 4 = 15
{[(I + 2) × 5] – 10} = 15 × 4 = 60
I + 2 = \(\frac{70}{5}\) = 14
(I + 2) × 5 = 60 + 10 = 70
I = 14 – 2 ; I = 12
Question 7.
Kamatchi, a fruit vendor sells 30 apples and 50 pomegranates. If she makes a profit of ? 8 per apple and loss ? 5 per pomegranate. What will be her overall profit or loss?
Solution:
Number of apples Kamatchi sold = 30
Profit per apple = ₹ 8(+)
∴ Profit for 30 apples = 30 × 8 = ₹ 240
Number of pomegranates sold 50
Loss per pomegranate = ₹ 5(-)
Loss on selling 50 pomegranates = 50 × (-5) = ₹ -250
Overall loss = -250 + 240 = ₹ -10
i.e. loss ₹ 10.
![]()
Question 8.
During a drought, the water level in a dam fell 3 inches per week for 6 consecutive weeks. What was the change in the water level in the dam at the end of this period?
Solution:
Water level fall per week = -3 inches
∴ Water level decrease for 6 weeks = 6 ₹ (-3) = 18 inches
∴ decrease of 18 inches of water level.
Question 9.
Buddha was born in 563 BC (BCE) and died in 483 BC (BCE). Was he alive in 500 BC (BCE)? and find his life time. (Source: Compton’s Encyclopedia)
Solution:
Years in BCC (BCE) are taken as negative integers.
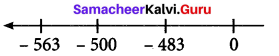
Buddha was bom in -563
and died in -483
So he was alive in 500 BC (BCE)
Life time = -483 – (-563) = -483 + 563 = +80
Buddha’s life time = 80 years.