You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.3
10th Maths Exercise 1.3 Samacheer Kalvi Question 1.
Let f = {(x, y)|x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Solution:
F = {(x, y)|x, y ∈ N and y = 2x}
x = {1, 2, 3,…}
y = {1 × 2, 2 × 2, 3 × 2, 4 × 2, 5 × 2 …}
R = {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10),…}
Domain of R = {1, 2, 3, 4,…},
Co-domain = {1, 2, 3…..}
Range of R = {2, 4, 6, 8, 10,…}
Yes, this relation is a function.
Exercise 1.3 Class 10 Maths Samacheer Question 2.
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x))|x ∈ X, f(x) = x2 + 1} is a function from X to N ?
Solution:
x = {3,4, 6, 8}
R = ((x, f(x))|x ∈ X, f(x) = X2 + 1}
f(x) = x2 + 1
f(3) = 32 + 1 = 10
f(4) = 42 + 1 = 17
f(6) = 62 + 1 = 37
f(8) = 82 + 1 = 65
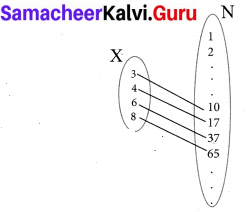
R = {(3, 10), (4, 17), (6, 37), (8, 65)}
R = {(3, 10), (4, 17), (6, 37), (8, 65)}
Yes, R is a function from X to N.
![]()
Ex 1.3 Class 10 Samacheer Question 3.
Given the function
f : x → x2 – 5x + 6, evaluate
(i) f(-1)
(ii) f(2 a)
(iii) f(2)
(iv) f(x – 1)
Answer:
f(x) = x2 – 5x + 6
(i) f (-1) = (-1)2 – 5 (-1) + 6 = 1 + 5 + 6 = 12
(ii) f (2a) = (2a)2 – 5 (2a) + 6 = 4a2 – 10a + 6
(iii) f(2) = 22 – 5(2) + 6 = 4 – 10 + 6 = 0
(iv) f(x – 1) = (x – 1)2 – 5 (x – 1) + 6
= x2 – 2x + 1 – 5x + 5 + 6
= x2 – 7x + 12
Samacheer Kalvi 10th Maths Exercise 1.3 Question 4.
A graph representing the function f(x) is given in figure it is clear that f(9) = 2.
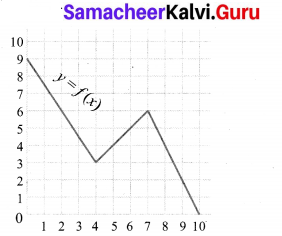
(i) Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
(ii) For what value of x is f (x) = 1?
(iii) Describe the following
(i) Domain
(ii) Range.
(iv) What is the image of 6 under f?
Solution:
From the graph
(a) f(0) = 9
(b) f(7) = 6
(c) f(2) = 6
(d) f(10) = 0
(ii) At x = 9.5, f(x) = 1
(iii) Domain = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
= {x |0 < x < 10, x ∈ R}
Range = {x|0 < x < 9, x ∈ R}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
(iv) The image of 6 under f is 5.
![]()
10th Maths Exercise 1.3 Question 5.
Let f(x) = 2x + 5. If x ≠ 0 then find \(\frac{f(x+2)-f(2)}{x}\)
Solution:
Given f(x) = 2x + 5, x ≠ 0.

10th Maths Exercise 1.3 Question 6.
A function fis defined by f(x) = 2x – 3
(i) find \(\frac{f(0)+f(1)}{2}\)
(ii) find x such that f(x) = 0.
(iii) find x such that f(x) = x.
(iv) find x such that f(x) = f(1 – x).
Solution:
Given f(x) = 2x – 3
(i) find \(\frac{f(0)+f(1)}{2}\)
f(0) = 2(0) – 3 = -3
f(1) = 2(1) – 3 = -1
∴ \(\frac{f(0)+f(1)}{2}=\frac{-3-1}{2}=\frac{-4}{2}\) = -2
(ii) f(x) = 0
⇒ 2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)
(iii) f(x) = x
⇒ 2x – 3 = x ⇒ 2x – x = 3
x = 3
(iv) f(x) = f(1 – x)
2x – 3 = 2(1 – x) – 3
2x – 3 = 2x – 2x – 3
2x + 2x = 2 – 3 + 3
4x = 2
x = \(\frac{2}{4}\)
x = \(\frac{1}{2}\)
0th Maths Relation And Function Question 7.
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown in figure. Express the volume V of the box as a function of x.
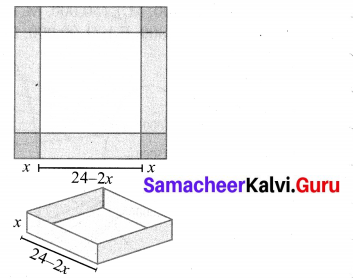
Solution:
Volume of the box = Volume of the cuboid
= l × b × h cu. units
Here l = 24 – 2x
b = 24 – 2x
h = x
∴ V = (24 – 2x) (24 – 2x) × x
= (576 – 48x – 48x + 4x2)x
V = 4x3 – 96x2 + 576x
10th Maths Ex 1.3 Question 8.
A function f is defined bv f(x) = 3 – 2x . Find x such that f(x2) = (f(x))2.
Solution:
f(x) = 3 – 2x
f(x2) = 3 – 2x2

![]()
10th Maths 1.3 Question 9.
A plane is flying at a speed of 500 km per hour. Express the distance d travelled by the plane as function of time r in hours.
Answer:
Speed of the plane = 500 km/hr
Distance travelled in “t” hours
= 500 × t (distance = speed × time)
= 500 t
10 Std Maths Exercise 1.3 Question 10.
The data in the adjacent table depicts the length of a woman’s forehand and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length(x) as y = ax + b, where a, b are constants.
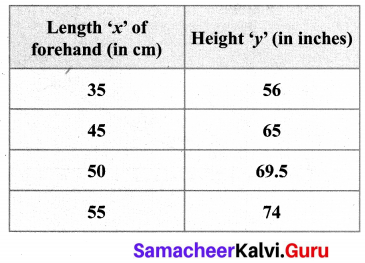
(i) Check if this relation is a function.
(ii) Find a and b.
(iii) Find the height of a woman whose forehand length is 40 cm.
(iv) Find the length of forehand of a woman if her height is 53.3 inches.
Solution:
(i) Given y = ax + b …………. (1)
The ordered pairs are R = {(35, 56) (45, 65) (50, 69.5) (55, 74)}
∴ Hence this relation is a function.
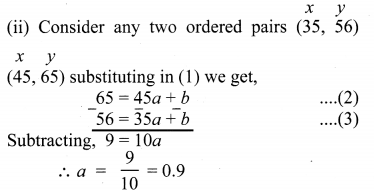
Substituting a = 0.9 in (2) we get
⇒ 65 = 45(.9) + b
⇒ 65 = 40.5 + b
⇒ b = 65 – 40.5
⇒ b = 24.5
∴ a = 0.9, b = 24.5
∴ y = 0.9x + 24.5
(iii) Given x = 40 , y = ?
∴ (4) → y = 0.9 (40) + 24.5
⇒ y = 36 + 24.5
⇒ y = 60.5 inches
(iv) Given y = 53.3 inches, x = ?
(4) → 53.3 = 0.9x + 24.5
⇒ 53.3 – 24.5 = 0.9x
⇒ 28.8 = 0.9x
⇒ x = \(\frac{28.8}{0.9}\) = 32 cm
∴ When y = 53.3 inches, x = 32 cm