You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.4
10th Maths Exercise 2.4 Samacheer Kalvi Question 1.
Find the next three terms of the following sequence.
(i) 8, 24, 72, …….
(ii) 5, 1, -3, …….
(iii) \(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \)………..
Solution:
(i) 8, 24, 72…
In an arithmetic sequence a = 8,
d = t1 – t1 = t3 – t2
= 24 – 8 72 – 24
= 16 ≠ 48
So, it is not an arithmetic sequence. In a geometric sequence,
r = \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
⇒ \(\frac{24}{8}=\frac{72}{24}\)
⇒ 3 = 3
∴ It is a geometric sequence
∴ The nth term of a G.P is tn = arn-1
∴ t4 = 8 × 34-1
= 8 × 33
= 8 × 27
= 216
t5 = 8 × 35-1
= 8 × 34
= 8 × 81
= 648
t6 = 8 × 36-1
= 8 × 35
= 8 × 243
= 1944
The next 3 terms are 8, 24, 72, 216, 648, 1944.
(ii) 5, 1, -3, …
d = t2 – t1 = t3 – t2
⇒ 1 – 5 = -3-1
-4 = -4 ∴ It is an A.P.
tn = a+(n – 1)d
t4 = 5 + 3 × – 4
= 5 – 12
= -7
15 = a + 4d
= 5 + 4 × -4
= 5 – 16
= -11
t6 = a + 5d
= 5 + 5 × – 4
= 5 – 20
= – 15
∴ The next three terms are 5, 1, -3, -7, -11, -15.
(iii) \(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \),………..
Here an = Numerators are natural numbers and denominators are squares of the next numbers
\(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \),\(\frac { 4 }{ 25 } \),\(\frac { 5 }{ 36 } \),\(\frac { 6 }{ 49 } \)………….
10th Maths Exercise 2.4 Question 2.
Find the first four terms of the sequences whose nth terms are given by
(i) an = n3 -2
Answer:
an = n3 – 2
a1 = 13 – 2 = 1 – 2 = -1
a2 = 23 – 2 = 8 – 2 = 6
a3 = 33 – 2 = 27 – 2 = 25
a4 = 43 – 2 = 64 – 2 = 62
The four terms are -1, 6, 25 and 62
(ii) an = (-1)n+1 n(n + 1)
Answer:
an = (-1)n+1 n(n + 1)
a1 = (-1)2 (1) (2) = 1 × 1 × 2 = 2
a2 = (-1)3 (2) (3) = -1 × 2 × 3 = -6
a3 = (-1)4 (3) (4) = 1 × 3 × 4 = 12
a4 = (-1)5 (4) (5) = -1 × 4 × 5 = -20
The four terms are 2, -6, 12 and -20
(iii) an = 2n2 – 6
Answer:
an = 2 n2 – 6
a1 = 2(1)2 – 6 = 2 – 6 = -4
a2 = 2(2)2 – 6 = 8 – 6 = 2
a3 = 2(3)2 – 6 = 18 – 6 = 12
a4 = 2(4)2 – 6 = 32 – 6 = 26
The four terms are -4, 2, 12, 26
Ex 2.4 Class 10 Samacheer Question 3.
Find the nth term of the following sequences
(i) 2, 5, 10, 17, ……….
(ii) 0, \(\frac { 1 }{ 2 } \), \(\frac { 2 }{ 3 } \),…..
(iii) 3, 8, 13, 18, ………
Solution:
(i) 2, 5, 10, 17
= 12 + 1, 22 + 1, 32 + 1, 42 + 1 ……….
∴ nth term is n2+1
(ii) 0, \(\frac { 1 }{ 2 } \),\(\frac { 2 }{ 3 } \),………….
= \(\frac { 1-1 }{ 1 } \),\(\frac { 2-1 }{ 2 } \),\(\frac { 3-1 }{ 3 } \)…..
⇒ \(\frac { n-1 }{ n } \)
∴ nth term is \(\frac { n-1 }{ n } \)
(iii) 3, 8, 13, 18
a = 3
d = 5
tn = a + (n – 1)d
= 3 + (n – 1)5
= 3 + 5n – 5
= 5n – 2
∴ nth term is 5n – 2
10th Maths Exercise 2.4 In Tamil Question 4.
Find the indicated terms of the sequences whose nth terms are given by
(i) an = \(\frac { 5n }{ n+2 } \) ; a6 and a13
(ii) an = -(n2 – 4); a4 and a11
Solution:
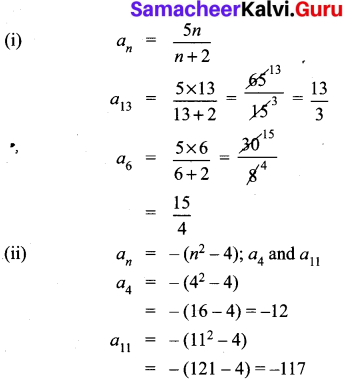
10th Maths 2.4 Exercise Question 5.
Find a8 and a15 whose nth term is

Solution:
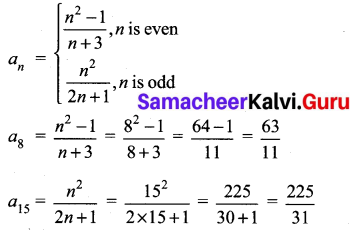
10th Maths 2.4 Question 6.
If a1 = 1, a2 = 1 and an = 2an-1 + an-2 n > 3, n ∈ N. Then find the first six terms of the sequence.
Answer:
a1 = a2 = 1
an = 2an-1 + an-2
a3 = 2a3-1 + a3-2 = 2a2 + a1
= 2(1) + 1 = 3
a4 = 2a4-1 + a4-2
= 2a3 + a2
= 2(3) + 1 = 6 + 1 = 7
a5 = 2 a5-1 + a5-2
= 2a4 + a3
= 2(7) + 3 = 17
a6 = 2a6-1 + a6-2
= 2a5 + a4
= 2(17) + 7
= 34 + 7 = 41
The sequence is 1, 1, 3, 7, 17,41, …