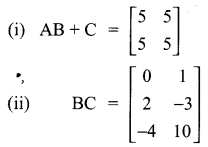You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.19
Multiple choice questions.
10th Maths Exercise 3.19 Answers Question 1.
A system of three linear equations in three variables is inconsistent if their planes
(1) intersect only at a point
(2) intersect in a line
(3) coincides with each other
(4) do not intersect.
Solution:
(4) do not intersect
10th Maths Exercise 3.19 Question 2.
The solution of the system x + y – 3z = – 6, -7y + 7z = 7, 3z = 9 is …………
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Answer:
(1) x = 1, y = 2, z = 3
Hint.
x + y – 3x = – 6 ….(1)
– 7y + 7z = 7 ….(2)
3z = 9 ….(3)
From (3) we get
z = \(\frac { 9 }{ 3 } \) = 3
Substitute the value of z in (2)
-7y + 7(3) = 7
-7y = -14
Substitute the value of y = 2 and z = 3 in (1)
x + 2 – 3(3) = -6
x + 2 – 9 = -6
x = -6 + 7
x = 1
The value of x = 1, y = 2 and z = 3
Exercise 3.19 Class 10 Question 3.
If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is
(1) 3
(2) 5
(3) 6
(4) 8
Solution:
(2) 5
Ex 3.19 Class 10 Question 4.

Solution:
(1) \(\frac{9 y}{7}\)
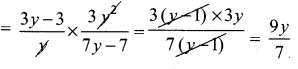
10th Maths 3.19 Question 5.
\(\mathbf{y}^{2}+\frac{\mathbf{1}}{y^{2}}\) is not equal to
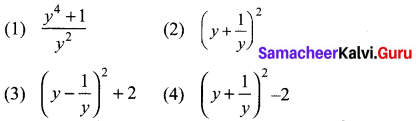
Solution:
(2) \(\left(y+\frac{1}{y}\right)^{2}\)
Hint:
\(y^{2}+\frac{1}{y^{2}} \neq\left[y+\frac{1}{y}\right]^{2}\)
Samacheer Kalvi Guru 10th Maths Question 6.

Solution:
(3) \(\frac{x^{2}-7 x+40}{(x+5)(x-5)(x+1)}\)
Hint:
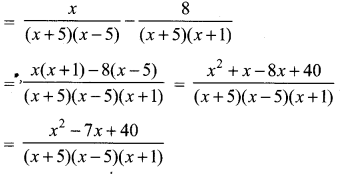
Samacheer Kalvi 10th Maths Book Graph Solution Question 7.
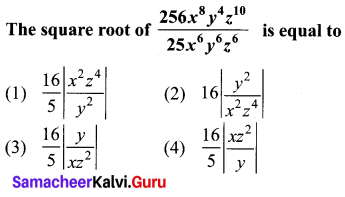
Solution:
(4) \(\frac{16}{5}\left|\frac{x z^{2}}{y}\right|\)
Hint:
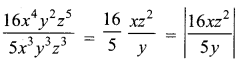
Exercise 3.19 Question 8.
Which of the following should be added to make x4 + 64 a perfect square ……….
(1) 4x2
(2) 16x2
(3) 8x2
(4) -8x2
Answer:
(2) 16x2
Hint.
x2 + 64 = (x2)2 + 82 – 2 × x2 × 8
= (x2 – 8)2
2 × x2 × 8 must be added
i.e, 16x2 must be added
Samacheer Kalvi 10th Maths Book Graph Solutions Question 9.
The solution of (2x – 1)2 = 9 is equal to
(1) -1
(2) 2
(3) -1, 2
(4) None of these
Solution:
(3) -1, 2
Hint:
(2x – 1)2 = (±3)2
⇒ 2x – 1 = +3
2x – 1 = 3, 2x – 1 = – 3
2x = 4, 2x = – 2
x = 2,-1
Question 10.
The values of a and b if 4x4 – 24x3 + 76x2 + ax + b is a perfect square are
(1) 100, 120
(2) 10, 12
(3) -120, 100
(4) 12, 10
Solution:
(3) -120, 100
Hint:

Question 11.
If the roots of the equation q2x2 + p2x + r2 = 0 are the squares of the roots of the equation qx2 +px + r = 0, then q,p, r are in ______.
(1) A.P
(2) G.P
(3) Both A.P and G.P
(4) none of these
Solution:
(2) G.P
Hint: q2x2 + p2x + r2 = 0
(2) G.P.
Question 12.
Graph of a linear polynomial is a …………..
(1) straight line
(2) circle
(3) parabola
(4) hyperbola
Answer:
(1) straight line
![]()
Question 13.
The number of points of intersection of the T quadratic polynomial x2 + 4x + 4 with the X axis.
(1) 0
(2) 1
(3) 0 or 1
(4) 2
Solution:
(2) 1
(x + 2)2 = (x + 2)(x + 2)
= x = -2, -2 = 1
Question 14.
For the given matrix A = \(\left[\begin{array}{cccc}{1} & {3} & {5} & {7} \\ {2} & {4} & {6} & {8} \\ {9} & {11} & {13} & {15}\end{array}\right]\) the order of the matrix AT is
(1) 2 × 3
(2) 3 × 2
(3) 3 × 4
(4) 4 × 3
Solution:
(3) 3 × 4
Hint:
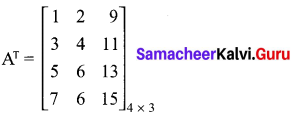
Question 15.
If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have
(1) 3
(2) 4
(3) 2
(4) 5
Solution:
(2) 4
Hint:
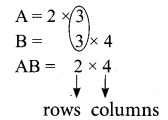
Question 16.
If a number of columns and rows are not equal in a matrix then it is said to be a …………..
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Answer:
(2) rectangular matrix
Question 17.
Transpose of a column matrix is
(1) unit matrix
(2) diagonal matrix
(3) column matrix
(4) row matrix
Solution:
(4) row matrix
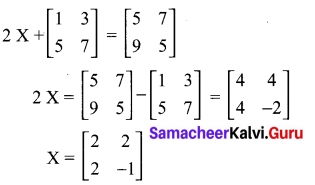
Question 18.

Solution:
(2) \(\left(\begin{array}{cc}{2} & {2} \\ {2} & {-1}\end{array}\right)\)
Hint:
Question 19.
Which of the following can be calculated from the given matrices
A = \(\left[\begin{array}{ll}{1} & {2} \\ {3} & {4} \\ {5} & {6}\end{array}\right]\), B = \(\left[\begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right]\)
(i) A2
(ii) B2
(iii) AB
(iv) BA
(1) (i) and (ii) only
(2) (ii) and (iiii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(3) (ii) and (iv) only
Hint:

Question 20.

(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(1) (i) and (ii) only
Hint: