You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.3
10th Maths Exercise 8.3 Samacheer Kalvi Question 1.
Write the sample space for tossing three coins using tree diagram.
Solution:
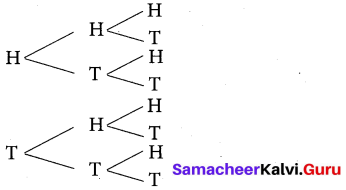
Ex 8.3 Class 10 Samacheer Question 2.
Write the sample space for selecting two balls from a bag containing 6 balls numbered 1 to 6 (using tree diagram).
Solution:
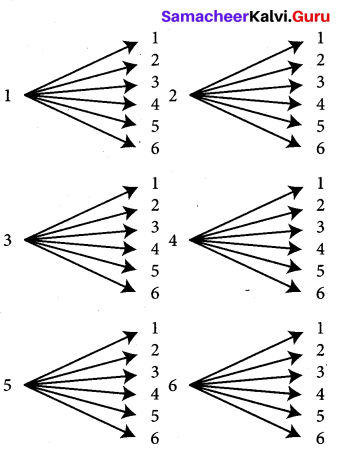
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
10th Maths Exercise 8.3 Question 3.
If A is an event of a random experiment such that P(A) : P(\(\overline{\mathbf{A}}\)) =17 : 15 and n(S) = 640 then find
(i) P(\(\overline{\mathbf{A}}\))
(ii) n(A).
Solution:
P(A): P(\(\overline{\mathbf{A}}\)) = 17 : 15

Exercise 8.3 Class 10 Samacheer Question 4.
A coin is tossed thrice. What is the probability of getting two consecutive tails?
Solution:
Outcomes {O}: {(HHH), (THH), (HTH), (HHT), (HTT), (THT), (TTH), (TTT)}
Two consecutive tails {F} : {(HTT), (TTH), (TTT)}
n{F} = 3
n{O} = 8

10th Maths 8.3 Solutions Question 5.
At a fete, cards bearing numbers 1 to 1000, one number on one card are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square number greater than 500, the player wins a prize. What is the probability that
(i) the first player wins a prize
(ii) the second player wins a prize if the first has won?
Answer:
Sample space = {1, 2, 3,… ,1000}
n(S) = 1000
(i) Let A be the event of setting square number greater than 500
A = {529, 576, 625, 676, 729, 784, 841, 900, 961}
n(A) = 9
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{9}{1000}\)
The probability that the first player wins prize = \(\frac{9}{1000}\)
(ii) If the first player wins, the number is excluded for the second player.
n(A) = 8 and n(S) = 999
P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{999}\)
Probability the second player wins a prize = \(\frac{8}{999}\)
10th Maths Probability Exercise 8.3 Question 6.
A bag contains 12 blue balls and x red balls. If one ball is drawn at random
(i) what is the probability that it will be a red ball?
(ii) If 8 more red balls are put in the bag, and if the probability of drawing a red ball will be twice that of the probability in (i), then find x.
Solution:
12 ➝ blue balls
x ➝ red balls
(i) P (red ball) = \(\frac{x}{x+12}\)
(ii) 8 red balls are added to the bag.
∴ 12 ➝ blue balls
x + 8 ➝ red balls
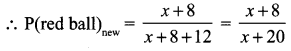
Given that P(ii) = 2 × P(i)
![]()
⇒ (x + 8)(x + 12) = 2x(x + 20)
⇒ (x2 + 20x + 96) = 2x2 + 40x
⇒ x2 + 20x – 96 = 0
⇒ x2 + 24x – 4x – 96 = 0
⇒ x(x + 24) – 4(x + 24) = 0
⇒ (x – 4)(x + 24) = 0
∴ x = 4 (or) x = -24
x cannot be negative ⇒ x = 4
Substituting x = 4 in (i),
![]()
10 Maths Exercise 8.3 Question 7.
Two unbiased dice are rolled once. Find the probability of getting
(i) a doublet (equal numbers on both dice)
(ii) the product as a prime number
(iii) the sum as a prime number
(iv) the sum as 1
Solution:
Doublet = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6,6)}
Total number of outcomes = 6 × 6
n(S) = 36
Number of favourable outcomes = 6
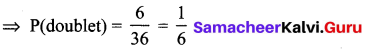
(ii) Number of favourable outcomes = 6
as favourable outcomes = (1, 2), (2, 1), (1, 3), (3, 1),(1, 5),and (5, 1)

(iii) Sum as prime numbers = {(1, 1), (1, 2), (2, 3), (1, 4), (1, 6), (4, 3), (5, 6)}
Number of favourable outcomes = 7
⇒ Probability = \(\frac{7}{36}\)
(iv) With two dice, minimum sum possible = 2
∴ Prob (sum as 1) = 0 [Impossible event]
10th Maths Exercise 8.4 Samacheer Kalvi Question 8.
Three fair coins are tossed together. Find the probability of getting
(i) all heads
(ii) atleast one tail
(iii) atmost one head
(iv) atmost two tails
Answer:
Three fair coins are tossed together
Sample spade = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
(i) Let A be the event of getting all heads
A = {HHH}
n(A) = 1
\(P(A)=\frac{n(A)}{n(S)}=\frac{1}{8}\)
(ii) Let B be the event of getting atleast one tail.
B = {HHT, HTH, HTT, THH, THT, TTH, TTT}
n(B) = 7
\(P(B)=\frac{n(B)}{n(S)}=\frac{7}{8}\)
(iii) Let C be the event of getting atmost one head
C = {HTT, THT, TTH, TTT}
n(C) = 4
\(P(C)=\frac{n(C)}{n(S)}=\frac{4}{8}=\frac{1}{2}\)
(iv) Let D be the event of getting atmost two tails.
D = {HTT, TTT, TTH, THT, THH, HHT, HTH}
n(D) = 7
\(P(D)=\frac{n(D)}{n(S)}=\frac{7}{8}\)
Class 10th Maths Ex 8.3 Solutions Question 9.
Two dice are numbered 1,2,3,4,5,6 and 1,1,2,2,3,3 respectively. They are rolled and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Solution:
Dice 1
S = {1,2, 3, 4, 5, 6}
Dice 2
S = {1,1,2, 2, 3, 3}
Total possible outcomes when they are rolled

n(S) = 36
Event of sum (2) = A = {(1,1), (1,1)},
n(A) = 2,P(A) = \(\frac{2}{36}\)
Event of sum 3 is B = {(1, 2), (1, 2), (2, 1), (2, 1)}
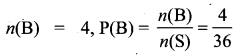
Event of sum 4 is C= {(1, 3), (1, 3), (2, 2), (2, 2), (3, 1) (3, 1)}
n(C) = 6
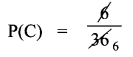
Event of getting the sum 5 is
D = {(2, 3), (2, 3), (3, 2), (3, 2), (4, 1), (4, 1)}
n(D) = 6, P(D) = \(\frac{6}{36}\) .
Event of getting the sum 6 is
E = {(3, 3), (3, 3), (4, 2), (4, 2), (5, 1), (5, 1)}
n(E) = 6, P(E) = \(\frac{6}{36}\)
Event of getting the sum 7 is
F = {(4, 3), (4, 3), (5, 2), (5, 2), (6, 1), (6, 1)}
n(F) = 6
P(F) = \(\frac{6}{36}\)
Event of getting the sum 8 is
G = {(5, 3), (5, 3), (6, 2), (6, 2)}
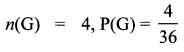
Event of getting the sum 9 is
H = {(6, 3), (6, 3), n(H) = 2

Class 10 Maths Chapter 8 Exercise 8.3 Question 10.
A bag contains 5 red balls, 6 white balls, 7 green balls, 8 black balls. One ball is drawn at random from the bag. Find the probability that the ball is drawn
(i) white
(ii) black or red
(iii) not white
(iv) neither white nor black
Solution:
5 red 6 white 7 green 8 black total no. of balls = 5 + 6 + 7 +8= 26

Class 10th Chapter 8 Exercise 8.3 Question 11.
In a box there are 20 non-defective and some defective bulbs. If the probability that a bulb selected at random from the box found to be defective is 3/8 then, find the number of defective bulbs.
Solution:
Let number of defective bulbs be ‘x’
Total number of bulbs = x + 20
![]()
⇒ 8x = 3x + 60
⇒ 5x = 60
⇒ x = 12
∴ No.of defective bulbs are = 12.
Ex 8.3 Class 10 Maths Solutions Question 12.
The king and queen of diamonds, queen and jack of hearts, jack and king of spades are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is
(i) a clavor
(ii) a queen of red card
(iii) a king of black card
Solution:
![]()
(i.e) remaining number of cards = 52 – 6 = 46 13
(i) P(a clavor) = \(\frac{13}{46}\)
(ii) P(queen of red card) = 0 as both Queen of diamond and heart have been removed.
(iii) only K of clavor is in the deck
⇒ P(king of black card) = \(\frac{1}{46}\)
8.3 Class 10 Question 13.
Some boys are playing a game, in which the stone was thrown by them landing in a circular region (given in the figure) is considered as a win and landing other than the circular region is considered as a loss. What’is the probability to win the game?
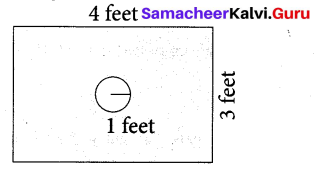
Solution:

Ex 8.3 Class 10 Question 14.
Two customers Priya and Amuthan are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another day. What is the probability that both will visit the shop on
(i) the same day
(ii) different days
(iii) consecutive days?
Solution:

Exercise 8.3 Class 10 Question 15.
In a game, the entry fee is ₹ 150. The game consists of tossing a coin 3 times. Dhana bought a ticket for entry. If one or two heads show, she gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise, she will lose. Find the probability that she
(i) gets double entry fee
(ii) just gets her entry fee
(iii) loses the entry fee.
Solution:
