The Samacheer Kalvi Class 11th Chemistry Solutions Chapter 6 Gaseous State Questions and Answers prevailing here are designed by the academic subject expertise in accordance with the state board prescribed syllabus and books. Aspirants who require help in preparing the Tamilnadu State Board Class 11th Chemistry Solutions Chapter 6 Gaseous State exercise questions can rely on the Samacheer Kalvi 11th Chemistry Solutions pdf for Chapter 6 Gaseous State given in this article.
Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 6 Gaseous State
Students who are excited for Tamilnadu State Board for Class 11th Chemistry Solutions Chapter 6 Gaseous State can find detailed and step wise solutions for all questions of Chapter 6 Gaseous State from here. Simply tap on the links available over here for which you have to view/download the Samacheer Kalvi Class 11th Solutions for Chemistry Solutions chapter 6 Gaseous State Questions and Answers. All these solutions are free to download and easy to access online or offline so that you can prepare well for the exams at any time.
Samacheer Kalvi 11th Chemistry Gaseous State Textual Evaluation Solved
I. Choose the correct answer from the following:
11th Chemistry Chapter 6 Book Back Answers Question 1.
Gases deviate from ideal behavior at high pressure. Which of the following statement (s) is correct for non – ideality?
(a) at high pressure the collision between the gas molecule become enormous
(b) at high pressure the gas molecules move only in one direction
(c) at high pressure, the volume of gas become insignificant
(d) at high pressure the inter molecular interactions become significant
Answer:
(d) at high pressure the inter molecular interactions become significant
11th Chemistry Lesson 6 Book Back Answers Question 2.
Rate of diffusion of a gas is …………
(a) directly proportional to its density
(b) directly proportional to its molecular weight
(c) directly proportional to its square root of its molecular weight
(d) inversely proportional to the square root of its molecular weight
Answer:
(d) inversely proportional to the square root of its molecular weight
11th Chemistry Unit 6 Book Back Answers Question 3.
Which of the following is the correct expression for the equation of state of van der Waals gas?

Answer:
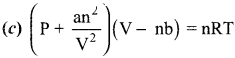
11th Chemistry Evaluate Yourself Answers Chapter 6 Question 4.
When an ideal gas undergoes unrestrained expansion, no cooling occurs because the molecules ………….
(a) are above inversion temperature
(b) exert no attractive forces on each other
(c) do work equal to the loss in kinetic energy
(d) colide without loss of energy
Answer:
(b) exert no attractive forces on each other
11th Chemistry Gaseous State Question 5.
Equal weights of methane and oxygen is mixed in an empty container at 298 K. The fraction of total pressure exerted by oxygen ………..
(a) 1/3
(b) 1/2
(c) 2/3
(d) 1/3 × 273 × 298
Answer:
(a) 1/3
Hint:
mass of methane = mass of oxygen = a
number of moles of methane = \(\frac {a}{16}\)
number of moles of Oxygen = \(\frac {a}{32}\)
mole fraction of Oxygen = 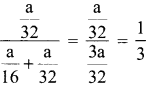
Partial pressure of oxygen = mole fraction x Total Pressure = \(\frac {1}{3}\)P
Gaseous State 11th Chemistry Question 6.
The temperatures at which real gases obey the ideal gas laws over a wide range of pressure is called …………
(a) Critical temperature
(b) Boyle temperature
(c) Inversion temperature
(d) Reduced temperature
Answer:
(b) Boyle temperature
Hint:
The temperature at which real gases obey the ideal gas laws over a wide range of pressure is called Boyle temperature
Gaseous State Class 11 Question 7.
In a closed room of 1000 m3 a perfume bottle is opened up. The room develops a smell. This is due to which property of gases?
(a) Viscosity
(b) Density
(c) Diffusion
(d) None
Answer:
(c) Diffusion
Samacheer Kalvi Guru 11th Chemistry Question 8.
A bottle of ammonia and a bottle of HCl connected through a long tube are opened simultaneously at both ends. The white ammonium chloride ring first formed will be ………….
(a) At the center of the tube
(b) Near the hydrogen chloride bottle
(c) Near the ammonia bottle
(d) Throughout the length of the tube
Answer:
(b) Near the hydrogen chloride bottle
Hint:
Rate of diffusion α 1/√m
mNH3 = 17
mHCl = 36.5
γNH3 > γHCl
Hence white fumes first formed near hydrogen chloride.
Gaseous State Class 11 Notes Pdf Question 9.
The value of universal gas constant depends upon ………..
(a) Temperature of the gas
(b) Volume of the gas
(c) Number of moles of the gas
(d) units of Pressure and volume
Answer:
(d) units of Pressure and volume
Samacheer Kalvi.Guru 11th Chemistry Question 10.
The value of the gas constant R is …………
(a) 0.082 dm3 atm.
(b) 0.987 cal mol-1 K-1
(c) 8.3 J mol-1K-1
(d) 8 erg mol-1K-1
Answer:
(c) 8.3 J mol-1K-1
Samacheer Kalvi Guru 11 Chemistry Question 11.
Use of hot air balloon in sports at meteorological observation is an application of
(a) Boyle’s law
(b) Newton’s law
(c) Kelvin’s law
(d) Brown’s law
Answer:
(a) Boyle’s law
Samacheerkalvi.Guru 11th Chemistry Question 12.
The table indicates the value of van der Waals constant ‘a’ in (dm3)2 atm. mol-2
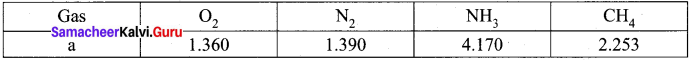
The gas which can be most easily liquefied is ………….
(a) O2
(b) N2
(c) NH3
(d) CH4
Answer:
(c) NH3
Hint:
Higher the value of ‘a’, greater the intermolecular force of attraction, easier the liquefaction. Option (c) is correct
Gaseous State Questions And Answers Pdf Question 13.
Consider the following statements.
(i) Atmospheric pressure is less at the top of a mountain than at sea level
(ii) Gases are much more compressible than solids or liquids
(iii) When the atmospheric pressure increases the height of the mercury column rises Select the correct statement.
(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (i), (ii) and (iii)
Answer:
(d) (i), (ii) and (iii)
11 Samacheer Chemistry Solutions Question 14.
Compressibility factor for CO2 at 400 K and 71.0 bar is 0.8697. The molar volume of CO2 under these conditions is ………..
(a) 22.04 dm3
(b) 2.24 dm3
(c) 0.41 dm3
(d) 19.5 dm3
Answer:
(c) 0.41 dm3
Compressibility factor (z) = \(\frac {Pv}{nRT}\)
V = \(\frac {z x nRT }{p}\)
![]()
V = 0.41 dm3
Samacheer Kalvi 11th Chemistry Solutions Question 15.
If temperature and volume of an ideal gas is increased to twice its values, the initial pressure P becomes ………….
(a) 4P
(b) 2P
(c) P
(d) 3P
Answer:
(c) P
Hint:

P2 = P2 Option (c)
Gaseous State Class 11 Questions Question 16.
At identical temperature and pressure, the rate of diffusion of hydrogen gas is 3\(\sqrt{3}\) times that of a hydrocarbon having molecular formula What is the value of n?
(a) 8
(b) 4
(c) 3
(d) 1
Answer:
(b) 4.
Hint:
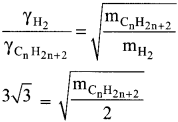
Squaring on both sides and rearranging
27 x 2 = mCnH2n-2
54 = n(12) + (2n-2)(l)
54 = 12n+2n – 2
54 = 14n – 2
n = (54 + 2)/14 = 56/14 = 4
Gaseous State Class 11 Pdf Question 17.
Equal moles of hydrogen and oxygen gases are placed in a container, with a pin-hole through which both can escape what fraction of oxygen escapes in the time required for one-half of the hydrogen to escape. (NEET phase 1)
(a) 3/8
(b) 1/2
(c) 1/8
(d) 1/4
Answer:
(c) 1/8
Hint:
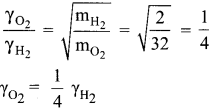
The fraction of oxygen that escapes in the time required for one half of the hydrogen to escape is 1/8
Question 18
The variation of volume V, with temperature T, keeping pressure constant is called the coefficient of thermal expansion ie α = \(\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_{P}\)For an ideal gas α is equal to ………..
(a) T
(b) 1/T
(c) P
(d) none of these
Answer:
(b) 1/T
Hint:

Question 19.
Four gases P, Q, R and S have almost same values of ‘b’ but their ‘a’ values (a, b are Van der Waals Constants) are in the order Q < R < S < P. At a particular temperature, among the four gases the most easily liquefiable one is ………….
(a) P
(b) Q
(c) R
(d) S
Answer:
(a) P
Hint:
Greater the ‘a’ value, casier the liquefaction
Question 20.
Maximum deviation from ideal gas is expected from (NEET)
(a) CH4(g)
(b) NH3(g)
(c) H2(g)
(d) N2(g)
Answer:
(b) NH3(g)
Question 21.
The units of Van der Waals constants ‘b’ and ‘a’ respectively
(a) mol L-1 and L atm2 mol-1
(b) mol L and L atm mol2
(c) mol-1 L and L2 atm mol-1
(d) none of these
Answer:
(c) mol-1 L and L2 atm mol-1
Hint:
an2/V2 atm
a = atm L2/mol2 = L2 mol-2 atm
nb = L
b = L /mol = L mol-1
Question 22.
Assertion : Critical temperature of CO2 is 304 K, it can be liquefied above 304 K.
Reason : For a given mass of gas, volume is to directly proportional to pressure at constant temperature.
(a) both assertion and reason arc true and reason is the correct explanation of assertion
(b) both assertion and reason are true but reason is not the correct explanation of assertion
(c) assertion is true but reason is false
(d) both assertion and reason are false
Answer:
(d) both assertion and reason are false
Hint:
Correct Statement: Critical temperature of CO2 is 304 K. It means that CO2 cannot be liquefied above 304 K, whatever the pressure may applied. Pressure is inversely proportional to volume.
Question 23.
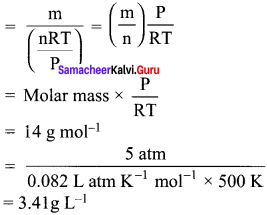
What is the density of N, gas at 227°C and 5.00 atm pressure? (R = 0.082 L atm K-1 mol-1)
(a) 1.40 g/L
(b) 2.81 g/L
(c) 3.41 g/L
(d) 0.29 g/L
Answer:
(c) 3.41 g/L
Hint:
Density = \(\frac {Mass}{Volume}\)
Question 24.
Which of the following diagrams correctly describes the behaviour of a fixed mass of an ideal gas ? (T is measured in K)
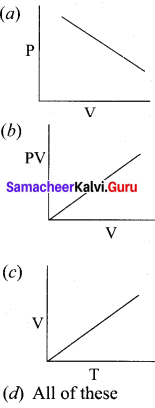
Answer:
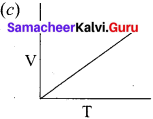
For a fixed mass of an ideal gas V α T
P α 1/V
and PV = Constant
Question 25.
25 g of each of the following gases are taken at 27°C and 600 mm Hg pressure. Which of these will have the least volume?
(a) HBr
(b) HCl
(c) HF
(d) HI
Answer:
(d) HI
Hint:
At a given temperature and pressure
Volume α number of moles
Volume α Mass / Molar mass
Volume α 28 / Molar mass
i.e. if molar mass is more , volume is less. Hence Hl has the least volume.
II. Answer these questions briefly.
Question 26.
State Boyle’s law.
Answer:
Boyle’s law states that at a given temperature. the volume occupied by a fixed mass of a gas is inversely proportional to its pressure.
V α \(\frac {1}{P}\);
where T and n are fixed or PV = Constant = k
Question 27.
A balloon filled with air at room temperature and cooled to a much lower temperalure can be used as a model for Charles’ law.
Answer:
Charles’ law:
- V T at constant P and n (or) \(\frac {V}{T}\) = Constant
- A balloon filled with air at room temperature and cooled to a much lower temperature. the size of the balloon is reduced. Because if the temperature of the gas decreases, the volume also decreases in a direct proportion.
- When temperature is reduced, the gas molecules inside in over slower due to decreased temperature and hence the volume decreases.
Question 28.
Name two items that can serve as a model for Gay Lussac’s law and explain.
Answer:
Gay Lussac’s law:
1. P α T at constant volume (or) = \(\frac {V}{T}\)
2. Example – 1:
You fill the car type completely full of air on the hottest day of summer. The type cannot change it shape and volume. But when winter comes, the pressure inside the lyre is reduced and the shape is also reduced. This confirms that pressure and temperature are direct related to each other.
3. Example – 2:
The egg in the bottle experiment.
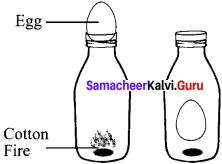
A glass bottle is taken, inside the bottle put some pieces of cotton with fire. Then place a boiled egg (shell removed) at the top of the bottle. The temperature inside the bottle increases from the fire, rising (he pressure. By scaling the bottle with egg, the fire goes on, dropping the temperature and pressure. This causes the egg to be sucked into the bottle.
P α T is proved (or) = \(\frac{P_{1}}{V_{1}}=\frac{P_{2}}{V_{2}}\)
Question 29.
Give the mathematical expression that relates gas volume and moles. Describe in words what the mathematical expression means.
Answer:
- The mathematical relationship betwêen the volume of a gas and the number of moles is V α n
- \(\frac{V_{1}}{n_{1}}=\frac{V_{2}}{n_{2}}\) = Constant
Where V1 and n1 are the volume and number of moles of a gas and V2 and n2 are the values of volume and number of moles of same gas at a different set of conditions. - If the volume of the gas increase then the number of moles of the gas also increases.
- At a certain temperature and pressure, the volume of a gas is dirctly proportional to the number of the moles of the gas.
Question 30.
What are ideal gases? In what way real gases differ from ideal gases.
Answer:
- Ideal gases are the gases that obey gas laws or gas equation PV = nRT.
- Real gases do not obey gas equation. PV = nRT.
- The deviation of real gases from ideal behaviour is measure in terms of a ratio of PV to nRT. This is termed as compression factor (Z). Z = \(\frac {PV}{nRT}\)
- For ideal gases Z = 1.
- For real gases Z > 1 or Z < 1. For example, at high pressure real gases have Z >1 and at intermediate pressure Z < 1.
- Above the Boyle point Z> 1 for real gases and below the Boyle point, the real gases first show a decrease for Z, reaches a minimum and then increases with the increase in pressure.
- So, it is clear that at low pressure and high temperature, the real gases behave as ideal gases.
Question 31.
Can a Van der Waals gas with a = 0 be liquefied? Explain.
Answer:
- a = 0 for a Van der Waals gas i.e. for a real gas. Van der Waals constant a = 0. It cannot be liquefied.
- If a = 0, there is a very less interaction between the molecules of gas.
- ‘a’ is the measure of strength of Van der Waals force of attraction between the molecules of the gas.
- If a is equal to zero, the Van der Waals force of attraction is very less and the gas cannot be liquefied.
Question 32.
Suppose there ¡s a tiny sticky area on the wan of a container of gas. Molecules hitting this area stick there permanently. Is the pressure greater or less than on the ordinary area of walls?
Answer:
- Molecules hitting the tiny sticky area on the wall of the container of gas moves faster as they get closer to adhesive surface, but this effect is not permanent.
- The pressure on the sticky wall is greater than on the ordinary area of walls.
Question 33.
Explain the following observations
(a) Aerated water bottles are kept under water during summer
(b) Liquid ammonia bottle is cooled before opening the seal
(c) The type of an automobile is inflated to slightly lesser pressure in summer than in winter
(d) The size of a weather balloon becomes larger and larger as it ascends up into larger altitude
Answer:
(a) In aerated water bottles, CO2 gas is passed through the aqueous solution under pressure because the solubility of the gas in water is not very high. In summer, the solubility of the gas in water is likely to decrease because of the rise in temperature. Thus, in summer, more of gas will be present above the liquid surface in the glass bottle.
In case, the pressure of the gas becomes too high, the glass will not be able to withstand the pressure and the bottle may explode. To avoid this, the bottles are kept under water. As a result, the temperature is likely to decrease and the solubility of CO2 is likely to increase in aqueous solution resulting in decreased pressure.
(b) Liquid ammonia bottle contains the gas under very high pressure. If the bottle is opened as such, then the sudden decrease in pressure will lead to a large increase in volume of the gas. As a result, the gas will come out of the bottle all of a sudden with force. This will lead to the breakage of the bottle and also causes accident.
However, if the bottle is cooled under tap water for sometime, there will be a decrease in the volume of a gas to a large extent. if the seal is opened now, the gas will corne out of the bottle at a slower rate, reduces the chances of accident.
(c) The pressure of air is directly proportional to the temperature. Since the temperature is higher in summer than in higher, the pressure of the air in the tube of the lyre is likely to be quite high as compared to winter. It is quite likely that the tube may burst under high pressure in summer, Therefore, it is advisable to inflate the types to lesser pressure in summer than in winter.
(d) The volume of the gas is inversely proportional to pressure at a given temperature according to Boyle’s law. As the weather balloon ascends, the pressure tends to decrease. As a result, the volume of the gas inside the balloon or the size of the balloon is likely to increase.
Question 34.
Give suitable explanation for the following facts about gases.
(a) Gases don’t settle at the bottom of a container
(b) Gases diffuse through all the space available to them and
(c) Explain with an increase in temperature
Answer:
(a) Gases by definition are the least dense state of matter. They have negligible intermolecular forces of attraction. So they are all free to roam separately. So the least dense gas particles will not sink at the bottom of a container.
(b) When a sample of a gas introduced to one part of a closed container, its molecules very quickly disperse throughout the container, this process by which molecules disperse in space in response to differences in concentration is called diffusion. For e.g., you can smell perfume in a room, because it difluses into the air totally inside the room.
(c) Diffusion is faster at higher temperature because the gas molecules have greater kinetic energy. Since heat increase the motion, then diffusion happens faster.
Question 35.
Suggest why there ¡s no hydrogen (H2) in our atmosphere. Why does the moon have no atmosphere?
Answer:
1. Hydrogen is the lightest element thus when produced in free state, it rises above all the other gases to the top of the atmosphere, where it is open to cosmic storms and solar flares. There it literally leaks from the atmosphere to the empty space. Hydrogen easily gains velocity required to escape Earth’s magnetic field. Hydrogen is very reactive in nature. So it would have reacted with O2 , in its way to produce H2O. So majority portion of H2 reacts and very less amount of it present in the upper level of atmosphere and gains velocity to escape the atmosphere.
2. Moon has no atmosphere because the value of acceleration due to gravity ‘g’ on the surface of the moon is small. Therefore, the value of escape velocity on the surface of the moon is very small. The molecule of the atmospheric gases on the surface of the moon have thermal velocities greater than the escape velocity. That’s why all the molecules of gases have escaped and there is no atmosphere in the moon. The moon has insufficient gravity to retain an atmosphere. So we conclude that moon has no atmosphere.
Question 36.
Explain whether a gas approaches ideal behaviour or deviates from ideal behaviour if –
(a) it is compressed to a smaller volume at constant temperature
(b) the temperature is raised while keeping the volume constant
(c) more gas is introduced into the same volume and at the same temperature
Answer:
(a) it a gas is compressed to a smaller volume at constant temperature, pressure is increased. At high pressure with a smaller volume, the gas deviates from ideal behaviour.
(b) If a gas temperature is raised keeping the volume constant, the pressure of the gas will increase. At high pressure, the gas deviates from ideal behaviour.
(c) if more gas is introduced into the same volume and at the same temperature, the number of moles are increasing. if the volume remains same, the increased number of moles collide with each other and kinetic energy increases and pressure decreases. At increased pressure, the gas deviates from ideal behaviour.
Question 37.
Which of the following gases would you expect to deviate from ¡deal behaviour under conditions of low temperature F Cl2, or Br2? Explain.
Answer:
1. Bromine deviates (Br2) from the ideal gas maximum than Cl2 and F2. Because Br2 has biggest size (atomic weight 79.9) provides maximum attraction between bromine molecules which is directly proportional to the size of the molecule and the boiling point of the liquid made from those molecules.
2. Br2 deviates from ideal behaviour because it has largest atomic radii compared to Cl2 and F2. So it contains more electrons than other two, and the Vander Waals forces are stronger in Br2 than in Cl2 and F2. So Br2 deviates from ideal behaviour.
Question 38.
Distinguish between diffusion and effusion.
Answer:
Diffusion:
- Diffusion is the spreading of molecules of a substance throughout a space or a second substance.
- Diffusion refers to the ability of the gases to mix with each other.
- E.g.. Spreading of something such as brown tea liquid spreading through the water in a tea cup.
Effusion:
- Effusion is the escape of gas molecules through a very small hole in a membrane into an evacuated area.
- Effusion is a ability of a gas to travel through a small pin-hole.
- E.g., pouring out something like the soap studs bubbling out from a bucket of water.
Question 39.
Aerosol cans carry clear warning of heating of the can. Why?
Answer:
Aerosol cans carry clear warning of heating of the can. As the temperature rises, pressure in the can will increase and ambient temperatures about 120°F may lead to explosions. So aerosol cans should always be stored in dry areas where they will not be exposed to excessive temperatures. You should never throw an aerosol can onto a fire or leave it in the direct sunlight. even it is empty. This is because the pressure will build up so much that the can will burst. It is due to 2 reasons.
- The gas pressure increases.
- More of the liquefied propellant turns into a gas.
Question 40.
When the driver of an automobile applies brake, the passengers are pushed toward the front of the car but a helium balloon is pushed toward back of the car. Upon forward acceleration the passengers are pushed toward the front of the car. Why?
Answer:
1. When the driver of an automobile applies brake, the passengers are pushed toward the front of the car due to inertia of the body, but a helium balloon pushed toward back of the car. Helium balloon responds to the air around it. Helium molecules are lighter than air of our atmosphere, and so they move toward back by gravity as a result of the accelerating frame.
2. Upon forward acceleration, the passengers arc pushed toward the front of the car, because the body in motion tends to stay in motion until acted upon by an outside force. Helium balloon is going to move opposite to this pseudo gravitational force.
Question 41.
Would it be easier to drink water with a straw on the top of Mount Everest?
Answer:
It is difficult to drink water with a straw on the top of Mount Everest. This is because the reduced atmospheric pressure is less effective in pushing water into the straw at the top of the mountain because gravity falls off gradually with height. The air pressure falls off, there isn’t enough atmospheric pressure to push the water up in the straw all the way to the mouth.
Question 42.
Write the Van der Waals equation for a real gas. Explain the correction term for pressure and volume.
Answer:
Van der Waals equation of state for real gases is –
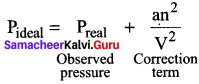
\(\left(P+\frac{a n^{2}}{V^{2}}\right)(V-n b)\) = nRT
Correction term for pressure:
\(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\) is the pressure correction. It represents the intermolecular interaction that causes the non ideal behaviour.
Correction term for Volume:
V – nb is the volume correction. it is the effective volume occupied by real gas.
Question 43.
Derive the values of critical constants from the Van der Waals constants.
Answer:
Derivation of critical constants from the Van der Waals constants:
Van der Waals equation is,
\(\left(P+\frac{a n^{2}}{V^{2}}\right)(V-n b)\) = nRT for 1 mole
From this equation, the values of critical constant PCVC and TC arc derived in terms of a and b the Van der Waals constants.
\(\left(P+\frac{a n^{2}}{V^{2}}\right)(V – b)\) = RT ………..(1)
On expanding the equestion (1)
P V + \(\frac {a}{V}\) – pb – \(\frac{\mathrm{ab}}{\mathrm{V}^{2}}\) – RT = 0 ………(2)
Multiplying eqestion (2) by \(\frac{V^{2}}{P}\),

equation (3) is rearranged in the powers of V
V3 – \(\left[\frac{\mathrm{RT}}{\mathrm{P}}+\mathrm{b}\right]\) V2 + \(\frac {aV}{P}\) –
= 0 ………..(4)
The above equation (4) is an cubic equation of V, which can have three roots. At the critical point. all the three values of V are equal to the critical volume VC.
i.e. V = VC.
V – VC = O ……….(5)
(V – VC)3 = O ………(6)
(V3 – 3VCV2 + 3VC3V – VC3 = 0 ………(7)
As the equation (4) is identical with equation (7), comparing the ‘V’ ternis in (4) and (7),

Divide equation (11) by (10)

When equation (12) is substituted in (10)
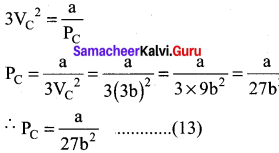
substituting the values of Vc and Pc in equation (9)

Critical constant a and b can be calculated using Van der Waals Constant as follows:

Question 44.
Why do astronauts have to wear protective suits when they are on the surface of moon?
Answer:
In space, there is no pressure, if we do wear a pressurised suit, our body will die. In space, we have to wear a pressurised suit, otherwise our body will continue to push out and blow up like a balloon. It would look cool, but we will be dead. So the astronauts in space must wear a pressurised suit (protective suits).
Question 45.
When ammonia combines with HCl, NH4 Cl is formed as white dense fumes. Why do more funies appear near HCl?
Answer:
- When ammonia combines with HCl, NH4 Cl is formed as white dense fumes. The reaction takes place in neutralization between a weak base and a strong acid.
- The property of the gas is diffusion.
- Diffusion of gases Ammonia and hydrogen chloride. Concentrated ammonia solution is placed on a pad in one end of a tube and concentrated HCl on the pad at the other. After about a minute, the gases diffuses far enough to meet and a ring of solid ammonium chloride is formed near the HCl end.
Question 46.
A sample of gas at 15°C at 1 atm has a volume of 2.58 dm3. Vhen the temperature is raised to 38°C at I atm does the volume of the gas increase? if so, calculate the final volume.
Answer:

V2 = 2.78 dm3 i.e. volume increased from 2.58 dm3 to 2.78 dm3.
Question 47.
A sample of gas has a volume of 8.5 dm3 at an unknown temperature. When the sample is submerged in ice water at 0°C, its volume gets reduced to 6.37 dm3. What ¡s its initial temperature?
Answer:

T1 = 364.28 K
Question 48.
Of two samples of nitrogen gas, sample A contains 1.5 moles of nitrogen in a vessel of volume of 37.6 dm3 at 298K, and the sample B is in a vessel of volume 16.5 dm3 at 298 K. Calculate the number of moles in sample B.
Answer:
nA = 1.5 mol nB = ?
VA = 37.6 dm3 VB = 16.5 dm3
(T = 298 K constant)
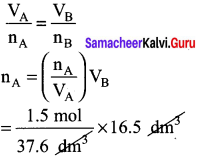
Question 49.
Sulphur hexafluoride is a colourless, odourless gas; calculate the pressure exerted by 1.82 moles of the gas in a steel vessel of volume 5.43 dm3 at 69.5°C, assuming ¡deal gas behaviour.
Answer:
n = 1.82 mole
V = 5.43 dm3
T = 69.5 + 273 = 342.5
P = ?
PV = nRT
P = \(\frac {nRT}{V}\)
![]()
P = 94.25 atm.
Question 50.
Argon is an inert gas used in light bulbs to retard the vapourlzation of the tungsten filament. A certain light bulb containing argon at 1.2 atm and 18°C is heated to 85°C at constant volume. Calculate its final pressure in atm.
Answer:
P1 = 1.2 atm
T1 = 18°C + 273 = 291 K
T2 = 85°C + 273 = 358 K
P2 = ?
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)

Question 51.
A small bubble rises from the bottom of a lake, where the temperature and pressure are 6°C and 4 atm. to the water surface, where the temperature is 25°C and pressure is 1 atm. Calculate the final volume in (mL) of the bubble, if its initial volume is 1.5 mL.
Answer:
T1 = 6°C + 273 = 279 K
P1 = 4 atm V1 = 1.5m
T2 = 25°C + 273 = 298 K
P2 = 1 atm V 1 = ?
\(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)

V2 = 6.41 mol.
Question 52.
Hydrochloric acid is treated with a metal to produce hydrogen gas. Suppose a student carries out this reaction and collects a volume of 154.4 x 10-3 dm3 of a gas at a pressure of 742 mm of Hg at a temperature of 298 K. What mass of hydrogen gas (in mg) did the student collect?
Answer:
V = 154.4 x 10-3dm3
P = 742 mm of Hg
T = 298 K m = ?
n = \(\frac{PV}{RT}\) = 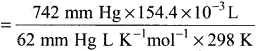
= 0.006 mol
n = \(\frac{PV}{RT}\)
n = \(\frac{Mass}{Molar Mass}\)
Mass = n x Molar mass
= 0.006 x 2.016
= 0.0121 g = 12.1 mg.
Question 53.
It takes 192 sec for an unknown gas to diffuse through a porous wall and 84 sec for N2 gas to effuse at the same temperature and pressure. What is the molar mass of the unknown gas?
Answer:
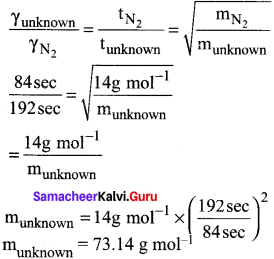
Question 54.
A tank contains a mixture of 52.5 g of oxygen and 65.1 g of CO2 at 300 K the total pressure in the tank ¡s 9.21 atm. Calculate the partial pressure (in atm.) of each gas in the mixture.
Answer:
mO2 = 52.5 g
PO2 = ?
mCO2 = 65.1 g
PCO2 = ?
T = 300 K P = 9.21 atm
PO2 = XO2 x total pressure

PO2 = XO2 x Total pressure
= 0.53 x 9.21 atm = 4.88 atm
PCO2 = XCO2 x Total pressure
= 0.47 x 9.21 atm = 4.33 atm
Question 55.
A combustible gas Is stored in a metal tank at a pressure of 2.98 atm at 25 °C. The tank can withstand a maximum pressure of 12 atm after which it will explode. The building in which the tank has been stored catches fire. Now predict whether the tank will blow up first or start melting? (Melting point of the metal = 1100 K).
Answer:
T1 = 298 K;
P1 = 2.98 atm;
T2 = 1100K;
P2 = ?
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
P2 = \(\frac{P_{1}}{T_{1}} \times T_{2}\)
= \(\frac{2.98 \mathrm{atm}}{298 \mathrm{K}} \times 1100 \mathrm{K}\) = 11 atm
At 1100 K, the pressure of the gas inside the tank will become 11 atm. Given that tank can withstand a maximum pressure of 12 atm, the tank will start melting first.
In Text Questions – Evaluate Yourself
Question 1.
Freon-I 2, the compound widely used in the refrigerator system as coolant causes depletion of ozone layer. Now It has been replaced by eco-friendly compounds. Consider 1.5 dm3 sample of gaseous freon at a pressure of 0.3 atm. If the pressure is changed to 1.2 atm. at a constant temperature, what will be the volume of the gas increased or decreased?
Answer:
Volume of freon (V1) = 1.5 dm3
Pressure (P1) = 0.3 atm
‘T’ is constant
P2 = 1.2 atm
V2 = ?
P1V1 = P2V2
V2 = \(\frac{P_{1} V_{1}}{P_{2}}\)

= 0.375 dm3
Volume decreased from 1.5 dm3 to 0.375 dm3
Question 2.
Inside a certain automobile engine, the volume of air in a cylinder is 0.375 dm3, when the pressure is 1.05 atm. When the gas is compressed to a volume of 0.125 dm3 at the same temperature, what is the pressure of the compressed air?
Answer:
V1 = 0.375dm3
V2 = 0.125 dm3
P1 = 1.05 atm
P2 = ?
T – Constant
P1V1 = P2V2
P2 = \(\frac{P_{1} V_{1}}{V_{2}}=\frac{10.5 \times 0.375}{0.125}\)
= 3.15 atm.
Question 3.
A sample of gas has a volume of 3.8 dm3 at an unknown temperature. When the sample is submerged in ice water at 0°C, its volume gets reduced to 2.27 dm3. What is its initial temperature?
Answer:
V1 = 3.8 dm3
T2 = 0°C = 273K
T1 = ? V2 = 2.27dm3
\(\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\)
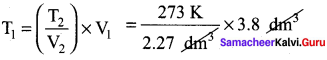
T1 = 457 K
Question 4.
An athlete in a kinesiology research study has his lung volume of 7.05 dm3 during a deep inhalation. At this volume the lungs contain 0.312 mole of air. During exhalation the volume of his Jung decreases to 2.35 dm3 How many moles of air does the athlete exhale during exhalation? (assume pressure and temperature remain constant)
Answer:
V1 = 7.05 dm3
V2 = 2.35 dm3
n1 = 0.312 mol
n1 =?
‘P’ and ‘T’ are constant
\(\frac{V_{1}}{n_{1}}=\frac{V_{2}}{n_{2}}\)

n2 = 0.104 mol
Number of moles exhaled = 0.312 – 0.104 = 0.208 moles
Question 5.
A small bubble rises from the bottom of a lake, where the temperature and pressure are 8° C and 6.4 atm. to the water surface, where the temperature ¡s 25°C and pressure is 1 atm. Calculate the final volume in (ml) of the bubble, if its initial volume is 2.1 ml.
Answer:
T1 = 8°C = 8 + 273 = 281K
P1 = 6.4atm V1 = 2.1 mol
T2 = 25°C = 25 + 273 = 298 K
P2 = 1 atm
V2 = ?
\(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)
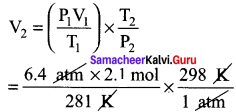
V2 = 14.25 ml
Question 6.
(a) A mixture of He and O2 were used ¡n the ‘air’ tanks of underwater divers for deep dives. For a particular dive 12 dm3 of O2 at 298 K, I atm. and 46 dm3 of He, at 298 K, 1 aim. were both pumped into a 5 dm3 tank. Calculate the partial pressure of each gas and the total pressure In the tank at 298 K
Answer:

P = 1 atm
Vtotal = 5 dm3
PO2 = XO2 x Ptotal

PHe = 3.54 atm
Question 6.
(b) A sample of solid KClO3 (potassium chlorate) was heated in a test tube to obtain O2 according to the reaction 2KClO3 → 2KCl(s) + 3O2 The oxygen gas was collected by downward displacement of water at 295 K. The total pressure of the mixture is 772 mm of Hg. The vapour pressure of water is 26.7 mn of Hg at 300K. What is the partial pressure of the oxygen gas?
Answer:
2KCl3(s) → 2KCl(s) 3O3(g)
Ptotal = 772 mm Hg
PH2O = 26.7 mm Hg
Ptotal = PO2 + PH2O
PO2 = Ptotal – PH2O
P1 = 26.7 mm Hg
T1 = 300 K
T2 = 295 K
P2 = ?
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
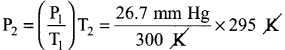
P2 = 26.26 mm Hg
∴ PO2 = 772 – 26.26
= 745.74 mm Hg
Question 7.
A flammable hydrocarbon gas of particular volume is found to diffuse through a small hole in 1.5 minutes. Under the same conditions of temperature and pressure an equal volume of bromine vapour takes 4.73 min to diffuse through the same hole. Calculate the molar mass of the unknown gas and suggest what this gas might be, (Given that molar mass of bromine = 159.8 g/ mole)
Answer:
t1 = 1.5 minutes (gas)hydrocarbon
t2 = 4.73 minutes (gas)Bromi
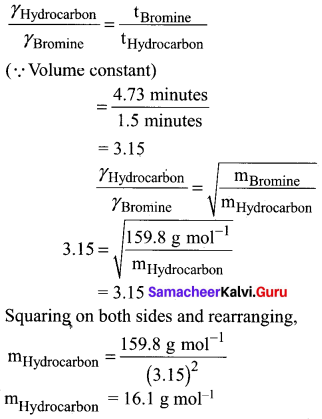
n (12) + (2n + 2) 1 = 16 (general formula for hydrocarbon CnH2n+2)
12n + 2n + 2 = 16
14n = 16 – 2
14n = 14
n = 1
The hydrocarbon is C1H2(1) + 2 = CH4
Question 8.
Critical temperature of H2O, NH3 and CO2 are 647.4, 405.5 and 304.2 K, respectively. When we start cooling from a temperature of 700 K which will liquefy first and which will liquefy finally?
Answer:
Critical temperature of a gas is defined as the temperature above which it cannot be liquefied even at high pressures.
∴ When cooling starts from 700 K, H2O vill liquefied first, then followed by ammonia and finally carbon dioxide will liquefied.
In-Text Example Problems
Question 9.
In the below figure, let us find the missing parameters [volume in (b) and pressure in (c)]
P1 = 1 atm P2 = 2 atm P3 = ? atm
V1 I dm3 V2 =? dm3 V3 = 0.25 dm3
T1 = 298 K T2 = 298 K T3 = 298 K
Solution:
According to Boyle’s law, at constant temperature for a given mass of gas at constant temperature,
P1V1 = P2V2 = P3V3
I atm x 1 dm3 = 2 atm x V2 = P3x 0.25 dm3
∴ 2 atm x V2 = 1 atm x 1 dm3
![]()
V2 = 0.5 dm3
and P3 x 0.25 dm3 = 1 atm x 1 dm3
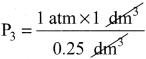
P3 = 4atm
Question 10.
In the below figure, let us find the missing parameters [volume in (b) and temperature in (c)]
P1 = 1 atm P2 = 1 atm P3 = 1 atm
V1 = 0.3dm3 V2 = ?dm3 V3 = 0.15dm3
T1 = 200K T2 = 300 K T3 = ? K
Answer:

According to Charles law,


T3 = 100k
Question 11.
Calculate the pressure exerted by 2 moles of sulphur hexafluoride in a steel vessel of volume 6 dm3 at 70°C assuming It is an ideal gas.
Answer:
We will use the ideal gas equation for this calculation as below:
P = \(\frac {nRT}{V}\)
![]()
= 9.39 atm.
Question 12.
A mixture of gases contains 4.76 mole of Ne, 0.74 mole of Ar and 2.5 mole of Xe. Calculate the partial pressure of gases, if the total pressure is 2 atm. at a fixed temperature. Solve this problem using Dalton’s law.
Answer:
PNe = XNe PTotal

PNe = XNe PTotal = 0.595 x 2 = 1.19 atm.
PNe = XNe PTotal = 0.093 x 2 = 0. 186 atm.
PNe = XNe PTotal = 0.312 x 2 = 0.624 atm.
Question 13.
An unknown gas diffuses at a rate of 0.5 time that of nitrogen at the same temperature and pressure. Calculate the molar mass of the unknown gas.
Answer:
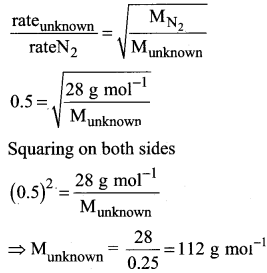
Question 14.
If a scuba diver takes a breath at the surface filling his lungs with 5.82 dm3 of air what volume will the air in his lungs occupy when he drives to a depth, where the pressure ¡s 1.92 atm. (assume temperature is constant and the pressure at the surface is exactly 1 atm.)
Solution :
Temperature = Constant
Pressure at the surface = 1 atm – P1
Pressure at the depth = 1.92 atm – P2
Vdlume of air breathing at the surface of the air = 5.82 dm3 – V1
Volume of air breathing at the depth = V2 = ?
![]()
V1 = 3.03 dm3
The volume of air scuba diver’s lung occupy = 3.03 dm3
Question 15.
Inside a certain automobile engine, the volume of air in a cylinder is 0.475 dm3, when the pressure is 1.05 atm. When the gas is compressed, the pressure increased to 5.65 atm. at the same temperature. What is the volume of compressed air?
Solution:
Volume of air in the cylinder 0.475 dm3 – V1
Pressure of air P1 = 1.05 atm
Increased pressure P2 = 5.65 atm
Volume of air compressed V2 = ?
P1V1 = P2V2
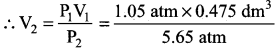
V2 = 0.08827 dm3
Compressed volume of air = 0.08 827 dm3
Samacheer Kalvi 11th Chemistry Gaseous State Additional Questions Solved
I. Choose the correct answer.
Question 1.
For one mole of a gas, the ideal gas equation is ………..
(a) PV = \(\frac {1}{2}\) RT
(b) PV = RT
(c) PV = \(\frac {3}{2}\)RT
(d) PV = \(\frac {5}{2}\)RT
Answer:
(b) PV= RT
Question 2.
The average kinetic energy of the gas molecule is …………
(a) inversely proportional to its absolute temperature
(b) directly proportional to its absolute temperature
(c) equal to the square of its absolute temperature
(d) All of the above
Answer:
(b) directly proportional to Its absolute temperature
Question 3.
Which of the following is the correct mathematical relation for Charles’ law at constant pressure?
(a) V ∝ T
(b) V ∝ t
(c) V ∝ – \(\frac {1}{T}\)
(d) all of above
Answer:
(a) V ∝ T
Question 4.
At constant temperature, the pressure of the gas is reduced to one-third, the volume
(a) reduce to one-third
(b) increases by three times
(c) remaining the same
(d) cannot be predicted
Answer:
(b) increases by three times
Question 5.
With rise in temperature, the surface tension of a liquid …………
(a) decreases
(b) increases
(c) remaining the same
(d) none of the above
Answer:
(a) decreases
Question 6.
Viscosity of a liquid is a measure of ……………
(a) repulsive forces between the liquid molecules
(b) frictional resistance
(c) intermolecular forces between the molecules
(d) none of the above
Answer:
(b) frictional resistance
Question 7.
The cleansing action of soaps and detergents is due to …………..
(a) internal friction
(b) high hydrogen bonding
(c) viscosity
(d) surface tensions
Answer:
(d) surface tensions
Question 8.
In Vander Waals equation of state for a non-ideal gas the net force of attraction among the molecules is given by ………..
(a) \(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\)
(b) P + \(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\)
(c) P – \(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\)
(d) – \(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\)
Answer:
(a) \(\frac{\mathrm{an}^{2}}{\mathrm{V}^{2}}\)
Question 9.
The compressibility factor, z for an ideal gas is ………….
(a) zero
(b) less than one
(c) greater than one
(d) equal to one
Answer:
(d) equal to one
Question 10.
Which of the following gases will have the lowest rate of diffusion?
(a) H2
(b) N2
(c) F2
(d) O2
Answer:
(c) F2
Question 11.
Which of the following is a mono atomic gas in nature?
(a) Oxygen
(b) Hydrogen
(c) Helium
(d) Ozone
Answer:
(c) Helium
Question 12.
Which of the following is a diatomic gas in nature?
(a) Oxygen
(b) Ozone
(c) Helium
(d) Radon
Answer:
(a) Oxygen
Question 13.
Which one of the following is not a monoatomic gas?
(a) Neon
(b) Xenon
(c) Argon
(d) Oxygen
Answer:
(d) Oxygen
Question 14.
Among the following groups which contains monoatomic gases?
(a) Group 17
(b) Group 18
(c) Group 1
(d) Group 15
Answer:
(b) Group 18
Question 15.
Which of the following is a tri atomic gas at room temperature?
(a) Oxygen
(b) Helium
(c) Ozone
(d) Nitrogen
Answer:
(c) Ozone
Question 16.
Which of the following gas is essential for our survival?
(a) N2
(b) H2
(c) O2
(d) He
Answer:
(c) O2
Question 17.
Among the following, which is deadly poison?
(a) CO2
(b) HCN
(c) HCl
(d) NH3
Answer:
(b) HCN
Question 18.
Which of the following is not chemically inert?
(a) Helium
(b) Oxygen
(c) Argon
(d) Krypton
Answer:
(b) Oxygen
Question 19.
Match the List-I and List-II using the correct code given below the list.

Answer:
![]()
Question 20.
Pressure of a gas is equal to ………..
(a) \(\frac {F}{a}\)
(b) F x a
(c) \(\frac {a}{F}\)
(d) F – a
Answer:
(a) \(\frac {F}{a}\)
Question 21.
The SI unit of pressure is ………..
(a) Nm-2 Kg-1
(b) Pascal
(c) bar
(d) atmosphere
Answer:
(b) Pascal
Question 22.
Statement-I: The pressure cooker takes more time for cooking at high altitude.
Statement-II: Air is subjected to Earth’s gravitational force. The pressure of air gradually decreases from the surface of the Earth to higher altitude.
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I
(e) Statement-I is wrong but Statement-II is correct
(ð) Statement-I is correct but Statement-II is wrong
Answer:
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I
Question 23.
The instrument used for measuring the atmospheric pressure is …………….
(a) lactometer
(b) barometer
(c) electrometer
(d) ammeter
Answer:
(b) barometer
Question 24.
The standard atmospheric pressure at sea level at 0°C is equal to ……………..
(a) 1 mm Hg
(b) 76 mm Hg
(c) 760 mm Hg
(d) 680 mm Hg
Answer:
(c) 760 mm Hg
Question 25.
Mathematical expression of Boyle’s law is ………….
(a) P1V1 = P2V2
(b) \(\frac {P}{V}\) = Constant
(c) \(\frac {V}{T}\) = Constant
(J) \(\frac {P}{T}\) = Constant
Answer:
(a) P1V1 = P2V2
Question 26.
Statement-I: If the volume of a fixed mass of a gas is reduced to half at constant temperature the gas pressure doubles.
Statement-II: If the volume is halved, the density of the gas is doubled.
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I
(c) Statement-I is correct but Statement-II is wrong
(d) Statement-I is wrong but Statement-II is correct
Answer:
(a) Statement-I and liare correct and Statement-II is the correct explanation of Statement-I
Question 27.
Which one of the following represents the Charles’ law?
(a) PV = Constant
(b) \(\frac {V}{T}\) = Constant
(c) VT Constant
(d) \(\frac {T}{V}\) = R
Answer:
(b) \(\frac {V}{T}\) = Constant
Question 28.
Which one of the following is absolute zero?
(a) 293 K
(b) 273 K
(c) – 273.15°C
(d) 0°C
Answer:
(c) – 273.15°C
Question 29.
\(\frac {P}{T}\) = Constant is known as …………..
(a) Boyle’s law
(b) Charles’ law
(c) Gay Lussac’s law
(d) Dalton’s law
Answer:
(c) Gay Lussac’s law
Question 30.
The ideal gas equation is …………..
(a) PV = RT for 1 mole
(b) P1 V1 = P2V2
(c) \(\frac {P}{T}\) = R
(d) P = P2 + P2 + P2
Answer:
(a) PV = RT for 1 mole
Question 31.
The value of Universal gas constant in a ideal gas equation is equal to ………….
(a) 8.3 14 KJ
(b) 0.082057 dm3 atm mol-1 K-1
(c) 1 Pascal
(d) 8.314 x 10-2Pascal
Answer:
(b) 0.082057 dm3 atm mol-1 K-1
Question 32.
Mathematical expression of Graham’ s law is ……………….

Answer:
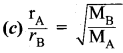
Question 33.
Which law is used in the isotopic separation of deuterium and protium?
(a) Boyle’s law
(b) Charles’ law
(c) Graham’ s law
(d) Gay Lussac’s law
Answer:
(c) Graham’ s law
Question 34.
The value of compression factor Z is equal to ………….
(a) \(\frac {nRT}{PV}\)
(b) \(\frac {PV}{RT}\)
(c) PV x nRT
(d) \(\frac {PV}{nRT}\)
Answer:
(d) \(\frac {PV}{nRT}\)
Question 35.
The value of critical volume is equal in terms of Vander Waals constant is ……….
(a) 3b
(b) \(\frac{8a}{27 Rb}\)
(c) \(\frac{a}{27 b^{2}}\)
(d) \(\frac{2a}{Rb}\)
Answer:
(a) 3b
Question 36.
The value of critical temperature of carbon dioxide is …………
(a) 273 K
(b) 303.98 K
(c) 373 K
(d) – 80°C
Answer:
(b) 303.98 K
Question 37.
Match the List-I and List-II using the correct code given below the list.


Answer:
![]()
Question 38.
The value of critical pressure of CO2 is ……………….
(a) 173 atm
(b) 73 atm
(c) 1 atm
(d) 22.4 atm
Answer:
(b) 73 atm
Question 39.
The temperature below which a gas obey Joule Thomson effect is called …………..
(a) critical temperature
(b) standard temperature
(c) inversion temperature
(d) normal temperature
Answer:
(c) Inversion temperature
Question 40.
The substance used in adiabatic process of liquefaction is ……………
(a) liquid helium
(b) gadolinium sulphate
(c) iron sulphate
(d) liquid ammonia
Answer:
(b) Gadolinium sulphate
Question 41.
The temperature produced in adiabatic process of liquefaction is …………..
(a) zero kelvin
(b) -273 K
(c) 10-4 K
(d) 104 K
Answer:
(c) 10-4 K
Question 42.
The molecules of a gas A travel four times faster than the molecules of gas B at same temperature. The ratio of molecular weight MA/ MB is ………….
(a) 1/16
(b) 4
(c) 1/4
(d) 16
Answer:
(a) 1/16
Question 43.
The compressibility factor for an ideal gas is …………….
(a) 1.5
(b) 2
(c) 1
(d) x
Answer:
(c) 1
Question 44.
Which of the following pair will diffuse at the same rate?
(a) CO2 and N2O
(b) CO2 and NO
(c) CO2 and CO
(d) N2O and NO
Answer:
(a) CO2 and N2O
Question 45.
The value of Vander Waals constant “a” is maximum for ……………….
(a) helium
(b) nitrogen
(c) methane
(d) ammonia
Answer:
(d) Ammonia
Question 46.
A person living in Shimla observed that cooking food with using pressure cooker takes more time. The reason for this observation is that at high altitude …………..
(a) pressure increases
(b) temperature decreases
(c) pressure decreases
(a) temperature decreases
Answer:
(c) pressure decreases
Question 47.
Statement-I : At constant temperature PV vs V plot for real gases is not a straight line.
Statement-II : At high pressure, all gases have Z >1, but at intermediate pressure most gases have Z <1.
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I
(c) Statement-I is correct but Statement-Il is wrong
(d) Statement-I is wrong but Statement-Il is correct .
Answer:
(a) Statement-I and liare correct and Statement-II is the correct explanation of Statement-I
Question 48.
Statement-I: Gases do not liquefy above their critical temperature, even on applying high press ure.
Statement-II: Above critical temperature, the molecular speed is high and intermolecular
attractions cannot hold the molecules together because they escape because of high speed.
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I
(c) Statement-I is correct but Statement-II is wrong
(d) Statement-I is wrong but Statement-II is correct
Answer:
(c) Statement-I and II are correct and Statement-IIs the correct explanation of Statement-I
Question 49.
The rate of diffusion of a gas is ………….
(a) directly proportional to its density
(b) directly proportional to its molecular mass
(c) directly proportional to its square root of its molecular mass
(d) inversely proportional to its square root of its molecular mass
Answer:
(d) inversely proportional to its square root of its molecular mass
Question 50.
In a closed flask of 5 liters, 1.0 g of H2 is heated from 300 to 600 K, which statement is not correct’?
(a) pressure of the gas increases
(b) the rate of the collusion increase
(c) the number of moles of gas increases
(d) the energy of gaseous molecules increases
Answer:
(c) the number of moles of gas increases
Question 51.
Match the List-I and List-II using the correct code given below the list.

Answer:
![]()
Question 52.
Consider the following statements.
(i) All the gases have higher densities than liquids and solids.
(ii) All gases occupy zero volume at absolute zero.
(iii) At very low pressure all gases exhibit ideal behaviour.
Which of the above statement is/are not correct?
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (ii) and (iii) only
Answer:
(a) (i) only
Question 53.
Which of the following gas is present maximum in atmospheric air?
(a) O2
(b) N2
(c) H2
(d) radon
Answer:
(b) N2
Question 54.
Which law is used in the process of enriching the isotope of U235 from other isotopes?
(a) Boyle’s law
(b) Dalton’s law of partial pressure
(c) Graham’s law of diffusion
(d) Charles’ law
Answer:
(c) Graham’s law of diffusion
Samacheer Kalvi 11th Chemistry Gaseous State 2 – Mark Questions
Question 1.
Identify the elements that are in gaseous state under normal atmospheric conditions.
Answer:
- Hydrogen, nitrogen, oxygen, fluorine and chlorine exist as gaseous diatomic molecules.
- Another form of oxygen namely ozone tr iatomic molecule exist as a gas at room temperature.
- Noble gases namely helium, neon, argon, krypton, xenon and radon are mono atomic gases.
Question 2.
Distinguish between a gas and a vapour.
Answer:
- Gas : A substance that is normally in a gaseous state at ordinary temperature and pressure. .,e.g., Hydrogen.
- Vapou r: The gaseous form of any substance that is a liquid or solid at normal temperature and pressure. e.g., At 298 K and 1 atm, water exist as water vapour.
Question 3.
Define pressure. Give its units.
Answer:
- Pressure is defined as the force exerted by a gas on unit area of the wall. Force F
- Pressure = \(\frac {Force}{Area}\) = \(\frac {F}{a}\)
- The SI unit of pressure is Pascal (Pa)
Question 4.
Define atmospheric pressure. What is its value?
Answer:
- The pressure exerted on a unit area of Earth by the colunm of air above it is called atmospheric pressure.
- The standard atmospheric pressure = 1 atm.
- 1 atm = 760 mm Hg.
Question 5.
Deep sea divers ascend slowly and breath continuously by time they reach the surface. Give reason.
Answer:
- For every 10 m of depth, a diver experiences an additional 1 atm of pressure due to the weight of water surrounding him.
- At 20 m, the diver experiences a total pressure of 3 atm. So the most important rule in diving is never hold breath.
- Divers must ascend slowly and breath continuously allowing the regulator to bring the air pressure in their lungs to 1 atm by the time they reach the surface.
Question 6.
Most aeroplanes cabins are artificially pressurized. Why?
Answer:
The pressure decreases with the increase in altitude because there are fewer molecules per unit volume of air. Above 9200 m (30,000 ft), for example, where most commercial aeroplanes fly, the pressure is so low that one could pass out for lack of oxygen. For this reason most aeroplanes cabins arc artificially pressurized.
Question 7.
What is the reason behind the cause of ear pain while climbing a mountain? How it can be rectified?
Answer:
- When one ascends a mountain in a plain, the external pressure drops while the pressure within the air cavities remains the same. This creates an imbalance.
- The greater internal pressure forces the eardrum to bulge outward causing pain.
- With time and with the help of a yawn or two, the excess air within your ear’s cavities escapes thereby equalizing the internal and external pressure and relieving the pain.
Question 8.
State Charles’ law.
Answer:
Charles’ law:
For a fixed mass of a gas constant pressure, the volume is directly proportional to temperature (K).
Mathematically V – T at constant P and n. (or) \(\frac {V}{T}\) = Constant (or) \(\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\) = Constant
Question 9.
What are the applications of Charles’ law?
Answer:
- A hot air inside the balloon rises because of its decreased density and causes the balloon to float inside the balloon rises because of its decreased density and causes the balloon to float.
- If you take a helium balloon outside on a chilly day, the balloon will crumble. Once you get back into warm area, the balloon will return to its original shape. This is because, in accordance with Charles’ law, a gas like helium takes up more space when it is warm.
Question 10.
State Avogadro’s hypothesis.
Answer:
Equal volumes of all gases under the same conditions of temperature and pressure contain equal number of molecules. Mathematically V ∝ n
\(\frac{V_{1}}{n_{1}}=\frac{V_{2}}{n_{2}}\) = Constant
Question 11.
Define Dalton’s law of partial pressure.
Answer:
Dalton’s law of partial pressure:
It states that the total pressure of a mixture of gases is the sum of partial pressures of the gases present.
Ptotal = P1 + P2 + P3
Question 12.
What are the applications of Dalton’s law of partial pressure?
Answer:
1. Physicians report the pressure of the patient’s gases in blood, analyzed by hospital lab, the values are reported as partial pressures.
Gas – Normal range
PCO2 35 – 45mm of Hg
PO2 80 – 100 mm of Hg
2. When gas is collected by downward displacement of water, the pressure of dry vapour collected is computed using Dalton’s law
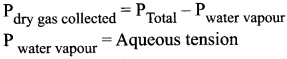
Question 13.
How can you identify a heavy smoker with the help of Dalton’s law?
Answer:
Physicians report the pressure of the patient’s gases in blood, analyzed by hospital lab. The values are reported as partial pressures.
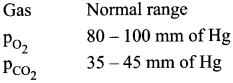
A heavy smoker may be expected to have low O2 and huge CO2 partial pressures.
Question 14.
Define Graham’s law of diffusion.
Answer:
Graham’s law of diffusion:
The rate of diffusion or effusion is inversely proportional to the square root of molecular mass of a gas through an orifice.
\(\frac{\mathrm{r}_{\mathrm{A}}}{\mathrm{r}_{\mathrm{B}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}}\)
rArB = rate of diffusion of gases A, B
MA, MB = Molecular mass of gases A, B
Question 15.
Helium diffuses more than air. Give reason.
Answer:
Take two balloons, one is filled with air and another with helium. After one day, the helium balloon was shrunk, because helium being lighter diffuses out faster than the air
Question 16.
Explain about the applications of Graham’s law of diffusion.
Answer:
- Graham’s law of diffusion is useful to determine the molecular mass of the gas if the rate of diffusion is known.
- Graham’s law forms the basis of the process of enriching the isotopes of U235 from other isotopes and also useful in isotopic separation of deuterium and protium.
Question 17.
What is compression factor?
Answer:
The deviation of real gases from ideal behaviour is measured in terms of a ratio of PV to nRT.
This is termed as compression factor.
Compression factor = Z = \(\frac {PV}{nRT}\)
For ideal gases Z = 1 at all temperature and pressures.
Question 18.
- Define critical temperature.
- What is the critical temperature of CO2 gas?
Answer:
- The temperature below which a gas can be liquefied by application of pressure is known as critical temperature.
- The critical temperature of CO2 gas is 303.98 K.
Question 19.
- Define critical pressure.
- What is the critical pressure of CO2 gas?
Answer:
- Critical temperature (PC) of a gas is defined as the minimum pressure required to liquefy.
- The critical pressure of CO2 is 73 atm.
Question 20.
CO2 gas cannot be liquefied at room temperature. Give reason.
Answer:
Only below the critical temperature, by the application of pressure, a gas can be liquefied. CO2 has critical temperature as 303.98 K. Room temperature means (30 + 273 K) 3O3 K. At room temperature, (critical temperature) even by applying large amount of pressure CO2 cannot be liquefied. Only below the critical temperature, it can be liquefied. At room temperature, CO2 remains as gas.
Question 21.
What is meant by Joule-Thomson effect?
Answer:
The phenomenon of lowering of temperature when a gas is made to expand adiabatically form a region of high pressure into a region of low pressure is known as Joule-Thomson effect.
Question 22.
Define inversion temperature.
Answer:
The temperature below which a gas obey Joule-Thomson effect is called inversion temperature (Ti).
Ti = \(\frac {2a}{Rb}\)
Question 23.
State and explain Boyle’s law. Represent the law graphically.
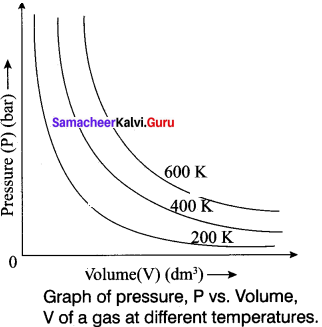
Answer:
It states that, the pressure of a fixed mass of a gas is inversely proportional to its volume if temperature is kept constant.
P – \(\frac {1}{V}\)
PV = Constant (n and T are constant)
P1v1 = P2V2
Graphical Representation:
Question 24.
Give an expression for the van der Waals equation. Give the significance of the constants used in the equation. What are their units?
Answer:
\(\left(P+\frac{n^{2} a}{V^{2}}\right)\) (V- nb) = nRT
Where n is the number of moles present and ‘a’’ b’ are known as van der Waals constants.
Significance of Van der Waals constants:
Van der Waals constant ‘a’:
‘a’ is related to the magnitude of the attractive forces among the molecules of a particular gas. Greater the value of’a’, more will be the attractive forces.
Unit of’a’ = L2 mol-2
Van der Waals constant ‘b’:
‘b’ determines the volume occupied by the gas molecules which depends upon size of molecule.
Unit of ‘b’ = L mol-1
Question 25.
What are ideal and real gases? Out of CO2 and NH3 gases, which is expected to show more deviation from the ideal gas behaviour?
Answer:
Ideal gas:
A gas that follows Boyle’s law, Charles’ law and Avogadro law strictly is called an ideal gas. It is assumed that intermolecular forces are not present between the molecules of an ideal gas.
Real gases:
Gases which deviate from ideal gas behaviour are known as real gases. NH3 is expected to show more deviation. Since NH3 is polar in nature and it can be liquefied easily.
Samacheer Kalvi 11th Chemistry Gaseous State 3 – Mark Questions
Question 1.
Explain the graphical representation of Boyle’s law.
Answer:
Boyle’s law states that at a given temperature the volume occupied by a fixed mass of a gas is inversely proportional to its pressure. V ∝ (T and n are fixed) .
If the pressure of the gas increases, volume will decrease and if the pressure of the gas decreases, the volume will increase. So PV = Constant.
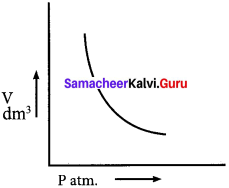
Question 2.
What are the consequences of Boyle’s law?
Answer:
1. if the volume of a fixed mass of a gas is reduced to half at constant temperature the gas pressure doubles.
2. Boyle’s law also helps to relate pressure to density.
P1V1 = P3V3 (Boyle’s law)
\(P_{1} \frac{m}{d_{1}}=P_{2} \frac{m}{d_{2}}\)
Where ‘m’ is the mass, d1 and d2 are the densities of gases at pressure P1 and P2. The density of the gas is directly proportional to pressure.
Question 3.
Explain Charles’ law with an experimental illustration.
Answer:
Charles’ law states that for a fixed mass of a gas at constant pressure, the volume is directly proportional to temperature (K).
V ∝ T (or) \(\frac {V}{T}\) = Constant

Volume vs Temperature:
If a balloon is moved from an ice water bath to a boiling water bath, the gas molecules inside move faster due to increased temperature and hence the volume increases.
Question 4.
Explain the graphical representation of Charles’ law.
Answer:
1. Variation of volume of the gas sample with temperature at constant pressure.
2. Each line (iso bar) represents the variation of volume with temperature at certain pressure. The pressure increases from P1 to P5.
3. i.e. P1<P2 < P3 <P4 < P5 . When these lines are extrapolated to zero volume, they intersect at a temperature of -273.15°C.
4. All gases are becoming liquids, if they are cooled to sufficiently low temperatures.
5. In other words, all gases occupy zero volume at absolute zero. So the volume of a gas can be measured over only a limited temperature range.
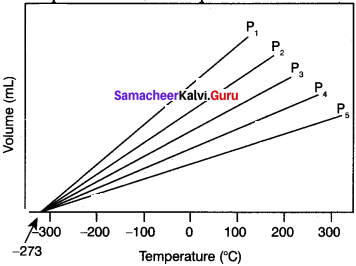
Question 5.
Explain graphicl representation of Gay Lussac’s law
Answer:
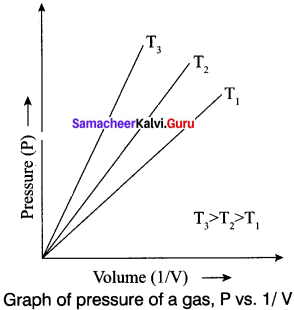
Gay Lussac’s law
At constant volume, the pressure of a fixed mass of a gas is directly proportional to temperature.
P – T (or) \(\frac {P}{T}\) = Constant
It can be graphically represented as shown here:
Lines in the pressure vs temperature graph are known as isochores (constant volume) of a gas.
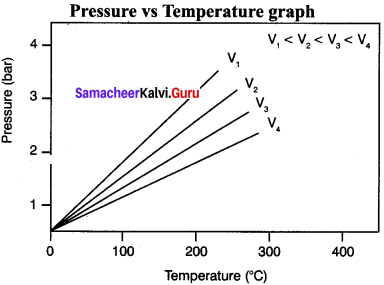
Question 6.
Explain the graphical representation of Avogadro’s hypothesis.
Answer:
Avogadros hypothesis states that equal volumes of all gases under the same conditions of temperature and pressure contain equaLnumbr of molecules.
V ∝ n
\(\frac{V_{1}}{n_{1}}=\frac{V_{2}}{n_{2}}\) = Constant.
Where V1 and are the volume and number 10- of moles of a gas and V2 and n2 are the different set of values of volume and number of moles of the same gas.
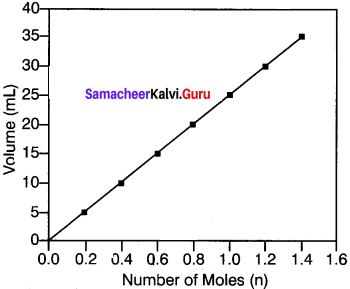
A better example to iflustrate Avogadro’s Number of Moles (n) hypothesis is to observe the effect of pumping more gas into a balloon. When more gas molecules (particularly CO2) are passed, the volume of the balloon increases. The pressure and temperature stay constant as the balloon inflates, so the increase in volume is due to the increase in the quantity of gas inside the balloon.
Question 7.
Derive ideal gas equation.
Answer:
The gaseous state is described completely using the following four variables T, P, V and n. Each gas law relates one variable of a gaseous sample to another while the other two variables are held constant. Therefore, combining all equations into a single equation will enable to account for the change in any or all of the variables.
Boyle’s law: V ∝ \(\frac{1}{P}\)
Charles’ law: V ∝ T
Avogadro’s law: V ∝ n
We can combine these equations into the following general equation that describes the physical
behaviour of all gases.
V ∝ \(\frac{nT}{P}\)
V = \(\frac{nRT}{P}\)
V = , where R = Proportionately constant.
The above equation can be rearranged to give PV = nRT – Ideal gas equation. Where, R is also known as Universal gas constant.
Question 8.
Derive the various values of R, gas constant.
Answer:
1. For standard conditions in which P is 1 atm, volume 22.4 14 dm3 for 1 mole at 273.15 K.
![]()
= 0.08205 7 dm3 atm mol-1 K-1
2. Where P = 105 Pascal, V = 22.71 x 10-3 m3 for I mole of a gas at 273.15 K.
![]()
= 8.314 pa m3 K-1 mol-1
=8.314x 10-2bar dm3 K-1mol-1
R = 8.314 J K-1 mol-1.
Question 9.
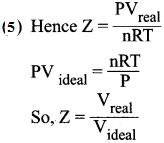
What is meant by Boyle temperature (or) Boyle point? How is it related with compression point?
Answer:
(1) Over a range of low pressures, the real gases can behave ideally at a particular temperature called as Boyle temperature or Boyle point.
(2) The Boyle point varies with the nattirc of the gas.
(3) Above the Boyle point, the compression point Z > 1 for real gases i.e. real gases show positive deviation.
(4) Below the Boyle point, the real gases first show a decrease for Z, reaches a minimum and then increase with increase in pressure. So, it is clear that at low pressure and at high temperature, the real gases behave as ideal gases.
Question 10.
Explain the different methods used for liquefaction of gases.
Answer:
- Linde’s method: Joule-Thomson effect is used to get liquid air or any other gas.
- Claude’s process: In addition to Joule-Thomson effect, the gas is allowed to perform mechanical work so that more cooling is produced.
- Adiabatic process: This method of cooling is produced by removing the magnetic property of magnetic material e.g. Gadolinium sulphate. By this method, a temperature of 10-4 K i.e. as low as zero Kelvin can be achieved.
Samacheer Kalvi 11th Chemistry Gaseous State 5 – Mark Question
Question 1.
How CH4 He and NH3 are deviating from ideal behaviour? (or) Explain how real gases deviate from ideal behaviour.
Answer:
1. The gases which obeys gas equation PV = nRT are known as ideal gases. The gases which do not obey PV = nRT are known as real gases.
2. The gas laws and the kinetic theory are based on the assumption that molecules in the gas phase occupy negligible volume (assumption 1) and that they do not exert any force on one another either attractive or repulsive (assumption 2). Gases whose behaviour is consistent with these assumptions are said to exhibit ideal behaviour.
3. The following graph shows RT plotted against P for three real gases and an ideal gas at a given temperature.
4. According to ideal gas equation, PV/RT is equal to n. Plot PV/RT versus P for ‘n’ moles oigas at 0°C. For1 mole of an ideal gas PV/ RT is equal to 1 irrespective of the pressure of the gas.
5. For real gases, we observe various deviations from ideal behaviour at high pressure. At very low pressure, all gases exhibit ideal behaviour, ie. PV/RT values all converge to n as P approaches zero.
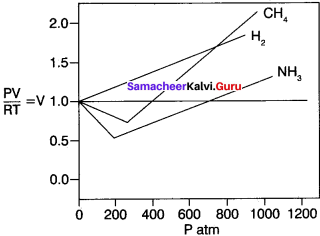
6. For real gases, this is true only at moderate low pressures. (≤ 5 atm) significant variation occurs as the pressure increases. Attractive forces operate among molecules at relatively short deviation.
7. At atmospheric pressure, the molecules in a gas are far apart and attractive forces arc negligible. At high pressure, the density of the gas increases and the molecules are much closer to one another. Intermolecular forces can be significant enough to affect the motion of the molecules and the gas will not behave ideally.
Question 2.
Derive Van der Waals equation of state.
Answer:
1. Consider the effect of intermolecular forces on the pressure exerted by a gas form the following explanation.
2. The speed of a molecule that is moving toward the wall of a container is reduced by the attractive forces exerted by its neighbours. Hence, the measured gas pressure is Q lower than the pressure the gas would exert, if it behave ideally.
Where ‘a’ is the proportionality constant and depends on the nature of the gas and n and V are the number of moles and volume of the container and respectively an2/ V2 is the correction term.
3. The frequency of encounters increases with the square of the number of molecules per unit volume n2/ V2. Therefore an2/ V2 represents the intermolecular interaction that causes non-ideal behaviour.
4. Another correction is concerned with the volume ¿ccupied by the gas molecules. ‘V’ represents the volume of the container. As every individual molecule of a real gas occupies certain volume, the effective volume V- nb which is the actually available for the gas, n is the number of moles and b is a constant of gas.
5. Hence Van der Waals equation of state for real gases are given as \(\left(P+\frac{a n^{2}}{V^{2}}\right)\) (V – nb) = nRT Where a and b are Van der Waals constants.
Question 3.
Explain about Andrew’s experimental isotherms of CO2 gas.
Answer:
1. Andrew plotted isotherms of carbon dioxide at different temperatures. it is then proved that many real gases behave in a similar manner like CO2.
2. At a temperature of 303.98 K, CO2 remains as a gas. Below this temperature, CO2, turns into liquid CO2 at 7 3atm. It is called the critical temperature of CO2.

3. At 303.98 K and 73 atm pressure, CO3,, becomes a liquid but remains a gas at higher temperature.
4. Below the critical temperature, the behaviour of CO2 is different. For example, consider an isotherm of CO2 at 294.5 K, it is a gas until the point B, is reached. At B, a liquid separates along the line BC, both the liquid and gas co-exist. At C, the gas is completely condensed.
5. If the pressure is higher than at C, only the liquid is compressed so, a steep rise in pressure is observed. Thus, there exist a continuity of state.
6. A gas below the critical temperature can be liquefied by applying pressures.
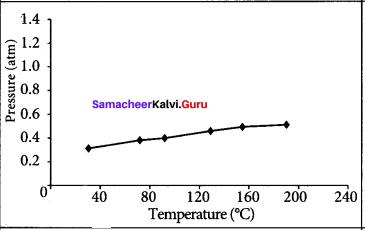
Activity – 1
The table below contains the values of pressure measured at different temperatures for 1 moie of an ideal gas. Plot the values in a graph and verify the Gay Lussac’s law. [Lines in the pressure vs temperature graph are known as iso chores (constant volume) of a gas]

Solution:
Gay Lussac’s law at constant volume = \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
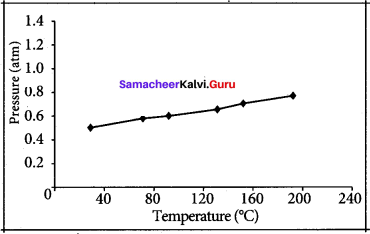
If temperature increases, pressure also increases.
So \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
We believe the provided Tamilnadu State Board for Class 11th Chemistry Solutions Chapter 6 Gaseous State Guide Pdf Free Download will benefit you. In case, do you have any questions regarding Samacheer Kalvi 11th Chemistry Solutions Book Solutions Chapter 6 Gaseous State Pdf, Questions and Answers, leave a comment below and we will get back to you at the earliest. Meanwhile, Bookmark our site for more information on State Board Solutions for various subjects.