Samacheer Kalvi 11th Computer Science Solutions Chapter 2 Number Systems

Students can Download Computer Science Chapter 2 Number Systems Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Computer Science Solutions Chapter 2 Number Systems

Samacheer Kalvi 11th Computer Science Number Systems Text Book Back Questions and Answers

PART – 1
I. Choose The Correct Answer

11th Computer Science Chapter 2 Book Back Answers Question 1.
Which refers to the number of bits processed by a computer’s CPU?
(a) Byte
(b) Nibble
(c) Word length
(d) Bit
Answer:
(c) Word length

Class 11 Computer Science Chapter 2 Question Answer Question 3.
Expansion for ASCII ………………..
(а) American School Code for Information Interchange
(b) American Standard Code for Information Interchange
(c) All Standard Code for Information Interchange
(d) American Society Code for Information Interchange
Answer:
(b) American Standard Code for Information Interchange

11th Computer Science 2nd Lesson Book Back Answers Question 4.
2^50 is referred as
(a) Kilo
(b) Tera
(c) Peta
(d) Zetta
Answer:
(c) Peta

Samacheer Kalvi Guru 11th Computer Science Question 5.
How many characters can be handled in Binary Coded Decimal System?
(a) 64
(b) 255
(c) 256
(d) 128
Answer:
(a) 64

11th Computer Science 2nd Lesson Question 6.
For 1101₂ what is the Hexadecimal equivalent?
(a) F
(b) E
(c) D
(d) B
Answer:
(c) D

Questions On Number System Class 11 Computer Science Question 7.
What is the 1’s complement of 00100110?
(a) 00100110
(b) 11011001
(c) 11010001
(d) 00101001
Answer:
(b) 11011001

Class 11 Computer Science Chapter 2 Pdf Question 8.
Which amongst this is not an Octal number?
(a) 645
(b) 234
(c) 876
(d) 123
Answer:
(c) 876

II. Short Answers

Class 11 Computer Science Chapter 2 Solutions Question 1.
What is data?
Answer:
The data is a fact about people, places, or some object. In a program, a value assigned to a variable is called data.

Samacheer Kalvi Guru 11 Computer Science Question 2.
Write the 1’s complement procedure.
Answer:
Step 1: convert given decimal number into Binary
Step 2: if the binary bit contains 8 bits if less add 0 at the left most bit, to make it 8 bits.
Step 3: Invert all the bits, (i.e.) change 1 as 0 and 0 as 1.

Samacheer Kalvi.Guru 11th Computer Science Question 3.
Convert (46)₁₀ into a Binary number
Answer:
(46)₁₀ into binary = 101110₂

Computer Science Chapter 2 Question 4.
We cannot find 1’s complement for (28)₁₀. State reason.
Answer:
Complement is only for negative numbers. (28)₁₀ is a positive number. So we can’t find 1’s complement.

Class 11 Computer Science Chapter 2 Notes Question 5.
List the encoding systems for characters in memory.
Answer:

1. BCD – Binary Coded Decimal
2. EBCDIC – Extended Binary Coded Decimal Interchange Code
3. ASCII – American Standard Code for Information Interchange
4. Unicode
5. ISCII – Indian standard code for information interchange

III. Explain in Brief

Question 1.
What is the radix of a number system? Give example.
Answer:
The radix refers to the base of a number system: the total number of possible digits. The decimal number system that we all use is base ten, as it has ten distinct digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Example: Binary system – Radix 2

Question 2.
Write a note on the binary number system.
Answer:
In Binary Number System, there are only two digits namely 0 and 1. The numbers in the binary system are represented to the base 2. In the Binary Number, the leftmost bit is the Most Significant Bit (MSB) and the rightmost bit is the Least Significant Bit (LSB). MSB has largest positional weight and LSB has the smallest positional weight.
Example: 110010₂

Question 3.
Convert (150)₁₀ into Binary, then convert that Binary number to Octal.
Step 1:
Change it to Binary.

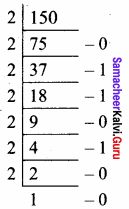
(150)₁₀ = 10010110

Step – 2:
Change it to Octal.

Answer:
Binary 10010110₂
Octal 226_g

Question 4.
Write a short note on ISCII.
Answer:
Indian Standard Code for Information Interchange (ISCII).
ISCII is the system of handling the character of Indian local languages. This is an 8-bit coding system. Therefore it can handle 256 (28) characters.

The supported scripts are:
Assamese, Bengali (Bangla), Devanagari, Gujarati, Gurmukhi, Kannada, Malayalam, Oriya, Tamil, and Telugu. ISCII does not encode the writing systems of India based on Arabic, but its writing system switching codes none the less provide for Kashmiri, Sindhi, Urdu, Persian, Pashto and Arabic. The Arabic – based writing systems were subsequently encoded in the PASCII encoding.

ISCII is an 8 – bit encoding. The lower 128 code points are plain ASCII, the upper 128 code points are ISCII – specific. In addition to the code points representing characters, ISCII makes use of a code point with mnemonic ATR that indicates that the following byte contains one of two kinds of information. One set of values changes the writing system until the next writing system indicator or end – of – line.

Question 5.
Add (a) – 22₁₀ + 15₁₀
(b) 20₁₀ + 25<sub>10

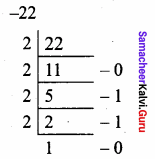
Answer:
(a) – 2210 = 101102
Binary Equivalent = 101102

Answer:
111110012</sub>

(b) 20₁₀ + 25₁₀
Answer:

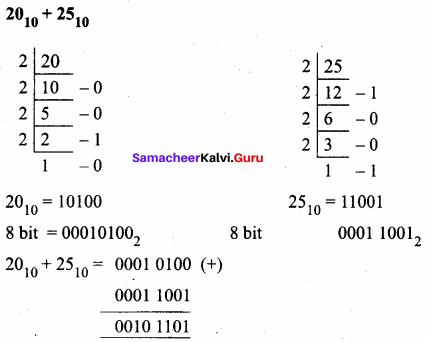
Answer:
00101101₂

IV. Detail Answers

Question 1.
(a) Write the procedure to convert fractional Decimal to Binary.
(b) Convert (98.46)₁₀ to Binary
Answer:
(а) Procedure to convert fractional Decimal to Binary.
Step 1: Multiply the decimal fraction by 2 and note the integer part. The integer part is either 0 or 1.
Step 2: Discard the integer part of the previous product. Multiply the fractional part of the previous product by 2. Repeat step 1 until the same fraction repeats or terminates (0).
Step 3: The resulting integer part forms a sequence of 0’s and 1 ’s that becomes the binary equivalent of a decimal fraction.
Step 4: The final answer is to be written from the first integer part obtained till the last integer part obtained.

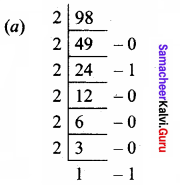
(b) Convert (98.46)₁₀ to Binary

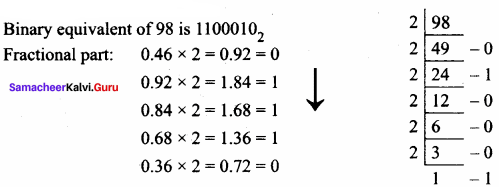
Answer:
1100010.01110 … ₂

Question 2.
Find 1’s Complement and 2’s Complement for the following Decimal number
(a) -98
(b) -135
Answer:

98₁₀ = 01100010
8 bit format = 01100010
1’s complement = 10011101
Add 1 bit = +1 = 10011110

135₁₀ = 10000111
1’st complement = 01111000
Add 1 bit = + 1
= 01111001

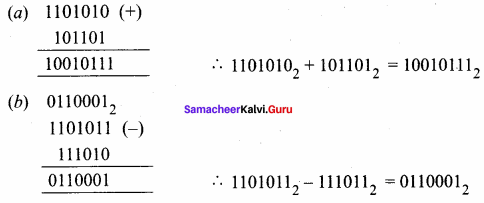
Question 3.
(a) Add 1101010₂ + 101101₂
(b) Subtract 1101011₂ – 111010₂
Answer:

PART – 1
I. Choose the correct answer

Question 1.
Which is a basic electronic circuit which operates on one or more signals?
(a) Boolean algebra
(b) Gate
(c) Fundamental gates
(d) Derived gates
Answer:
(b) Gate

Question 2.
Which gate is called the logical inverter?
(a) AND
(b) OR
(c) NOT
(d) XNOR
Answer:
(c) NOT

Question 3.
A + A = ?
(a) A
(b) O
(c) 1
(d) A
Answer:
(a) A

Question 4.
NOR is a combination of?
(a) NOT(OR)
(b) NOT(AND)
(c) NOT(NOT)
(d) NOT(NOR)
Answer:
(a) NOT(OR)

Question 5.
NAND is called as ……………… Gate.
(a) Fundamental Gate
(b) Derived Gate
(c) Logical Gate
(d) Electronic gate
Answer:
(b) Derived Gate

PART – 2
II. Short Answers

Question 1.
What is Boolean Algebra?
Answer:
Boolean algebra is a mathematical discipline that is used for designing digital circuits in a digital computer. It describes the relationship between inputs and outputs of a digital circuit.

Question 2.
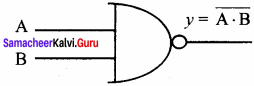
Write a short note on NAND Gate.
Answer:
The NAND gate is the combination of NOT and AND gates. The NAND gate is generated by inverting the output of a AND gate. The algebraic expression of the NAND is Y = \(\overline{\mathrm{A} . \mathrm{B}}\)

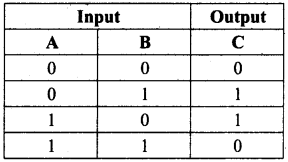
Question 3.
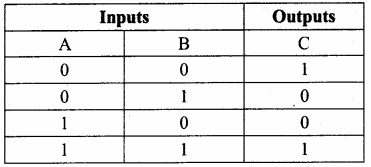
Draw the truth table for the XOR gate.
Answer:
The truth table for XOR gate is

Question 4.
Write the associative laws?
Answer:
Associative Laws:
i) A + (B + C) = (A + B) + C
ii) A . (B . C) = (A . B) . C

Question 5.
What are derived gates?
Answer:
Derived Gates are the gates that are derived from the fundamental gates.
Example: NAND, NOR, XOR, XNOR

PART – 3
III. Explain in Brief

Question 1.
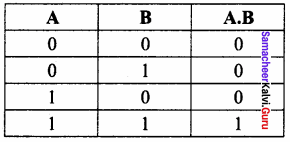
Write the truth table of fundamental gates.
Answer:
(a) AND gate – Truth Table

(b) OR gate – Truth Table

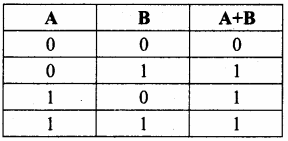
(c) NOT Gate – Truth Table

Question 2.
Write a short note on XNOR gate.
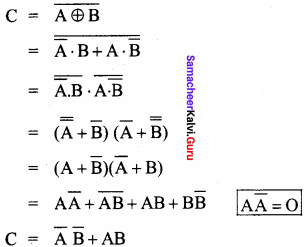
The XNOR (exclusive – NOR) gate is a combination of XOR gate followed by an inverter. Its output is “true” if the inputs are same and false if the inputs are different.
The output of XNOR is C = AB + \(\overline{\mathrm{A}}\) \(\overline{\mathrm{B}}\)
= A \(\odot\) B
Where \(\odot\) indicates included dot.
Truth Table:

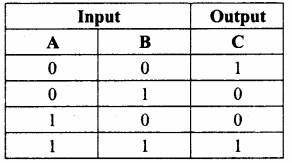
Logic symbol:

Logic circuit:

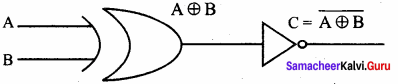
Question 3.
Reason out why the NAND and NOR are called universal gates?
Answer:
NAND and NOR gates are called Universal gates because the fundamental logic gates can be realized through them.

Question 4.
Give the truth table of XOR gate.
Answer:
XOR – Truth Table

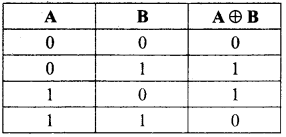
Question 5.
Write the De Morgan’s law.
Answer:
De Morgan’s laws
\(i) \overline{\mathrm{A}+\mathrm{B}}=\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}
ii) (\bar{A} \cdot B)=\bar{A}+\bar{B}\)

PART – 4
IV. Explain in Detail

Question 1.
Explain the fundamental gates with an expression and truth table.
Answer:
the gate is a basic electronic circuit that operates on one or more signals to produce an output signal.
The three fundamental gates are AND, OR, and NOT gates.

AND Gate:
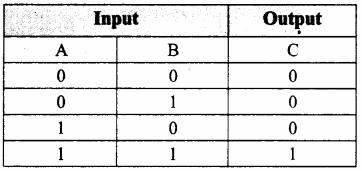
The AND gate can have two or more input signals and produce an output signal. The output is “true” only when both inputs are “true”, otherwise, the output is “false”. In other words, the output will be 1 if and only if both inputs are 1; otherwise, the output is 0. The output of the AND gate is represented by a variable say C, where A and B are two and if input boolean variables. In boolean algebra, a variable can take either of the values ‘0’ or ‘1’. The logical symbol of the AND gate is

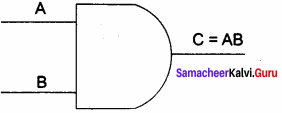
The truth table for AND gate is

OR Gate:
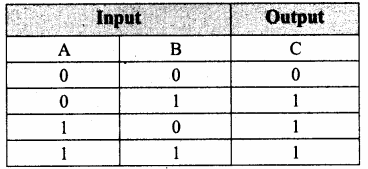
The OR gate gets its name from its behaviour like the logical inclusive “OR”. The output is “true” if either or both of the inputs are “true”. If both inputs are “false” then the output is “false”. In other words the output will be 1 if and only if one or both inputs are 1; otherwise, the output is 0. The logical symbol of the OR gate is

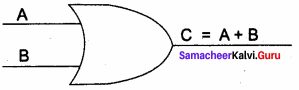
The truth table for OR gate is

NOT Gate:
The NOT gate, called a logical inverter, has only one input. It reverses the logical state. In other words, the output C is always the complement of the input. The logical symbol of the NOT gate is

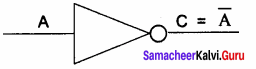
The truth table for NOT gate is

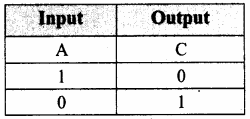
Question 2.
How AND and OR can be realized using NAND and NOR gate.
Bubbled AND Gate
(i) Realized of and using only AND gate:
The Boolean function for AND is C = AB. The same can be realized using only NAND gates.

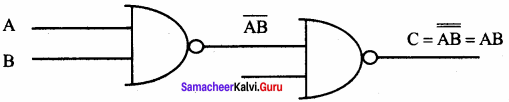
(ii) Realization of or using only NAND’s:
The Boolean function of OR is C = A + B. The same can be realized using only NAND gates.

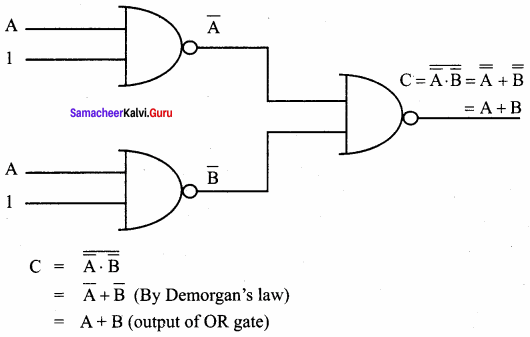
(iii) Realization of AND using NOR:
By using only the NOR gates, we can get the output equivalent to the output of AND gate.
C = A.B

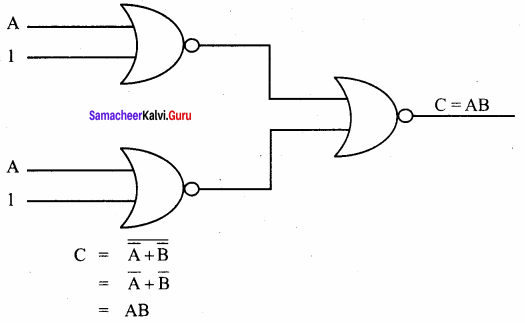
(iv) Realization of OR using NOR’s:
By using only NOR gates we are getting the output equivalent to OR gate.

Question 3.
Explain the Derived gates with expression and truth table.
Answer:
The logic gates like NAND, NOR, XOR, and XNOR are derived gates which are derived from the fundamental gates AND, OR NOT.

(i) NAND gate:
The NAND is the combination of NOT and AND. The NAND is generated by inverting the output of an AND operation.
Output: y = \(\overline{\mathrm{A}\mathrm{B}}\)
Logic circuit

Logic symbol:

Truth table:

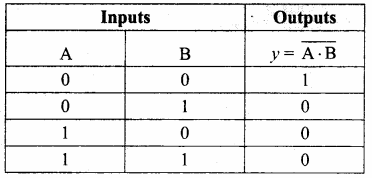
Inputs Outputs
(ii) NOR gate:
The NOR is the combination of NOT and OR. The NOR is generated by inverting the output of an OR operation.
Logic function: y = \(\overline{\mathrm{A}\mathrm{B}}\)
Logic circuit:

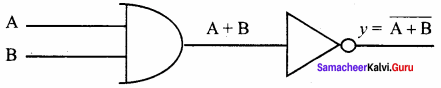
logic symbol:

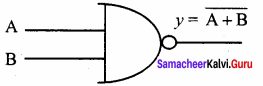
Truth table:

(iii) XOR gate:
The XOR (exclusive – OR) gate acts in the same way as the logical either /or.
Logic symbol:

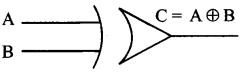
Logic circuit:

Truth table:

(iv) XNOR gate:
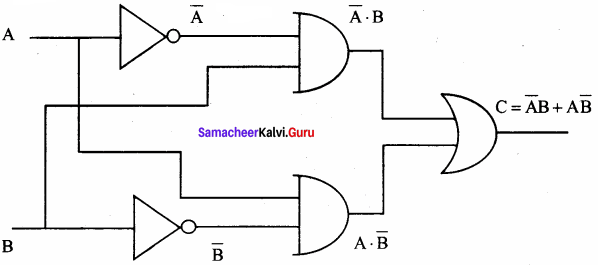
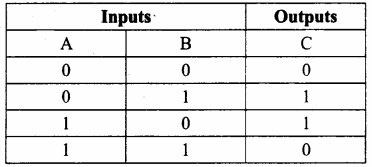
XNOR gate (exclusive – NOR) gate is a combination of XOR gate followed by an inverter.
Logic function: y = \(\overline{\mathrm{A}\mathrm{B}}\)

logic symbol:

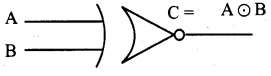
Truth table:

Boolean function:

Samacheer Kalvi 11th Computer Science Number Systems Additional Questions and Answers

PART – 1
I. Choose the correct answer

Question 1.
Computer handles data in the form of ________________
a) 1
b) 0
c) alphabets
d) both A and B
Answer:
d) both A and B

Question 2.
The term data comes from the word ………………..?
(a) number
(b) datum
(c) nibble
(d) bit
Answer:
(b) datum

Question 3.
0 and 1 are called________________
a) BIT
b) BYTE
c) NIBBLE
d) WORD
Answer:
a) BIT

Question 4.
……………….. scheme is denoted by hexadecimal numbers.
(a) binary
(b) Unicode
(c) word length
(d) data
Answer:
(b) Unicode

Question 5.
A_________ is the short form of Binary digit.
a) BIT
b) BYTE
c) NIBBLE
d) WORD
Answer:
a) BIT

Question 6.
A ……………….. number is represented using base 16.
(a) Hexadecimal
(b) octal
(c) binary
(d) decimal
Answer:
(a) Hexadecimal

Question 7.
A________ is a collection of 4 bits.
a) BIT
b) BYTE
c) NIBBLE
d) WORD
Answer:
c) NIBBLE

Question 8.
Octal number system uses digits ………………..
(a) 7
(b) 5
(c) 8
(d) 10
Answer:
(c) 8

Question 9.
The memory size of the computer is measured in the unit called __________
a) BIT
b) BYTE
c) NIBBLE
d) WORD
Answer:
b) BYTE

Question 10.
The NAND gate operates an AND gate followed by a ……………….. gate.
(a) AND
(b) OR
(c) NOT
(d) XOR
Answer:
(c) NOT

Question 11.
The word length of the present day computer is __________ bits.
a) 32
b) 64
c) 8
d) 32 or 64
Answer:
d) 32 or 64

Question 12.
Expand BIT.
(a) Basic Input Term
(b) Binary Input Term
(c) Binary Digit
(d) Binary Inverse Digit
Answer:
(c) Binary Digit

Question 13.
_________is not a valid word length of a computer.
a) 8
b) 12
c) 4
d) both B and C
Answer:
d) both B and C

Question 14.
Identify the wrong pair.
1. 1 YB = 2^80
2. 1 BM = 2^70
3. 1 MB = 2^20
4. 1 TM = 2^40
(a) 2
(b) 3
(c) 4
(d) 1
Answer:
(a) 2

Question 15.
1 MegaByte equals t______ KiloBytes.
a) 1024
b) 256
c) 1000
d) 128
Answer:
a) 1024

Question 16.
The collection of 4 bits is ………………..
(a) bit
(b) byte
(c) nibble
(d) KB
Answer:
(c) nibble

Question 17.
Match the following.

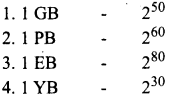
(a) 4 12 3
(b) 12 3 4
(c) 4 3 2 1
(d) 4 2 1 3
Answer:
(a) 4 12 3

Question 17.
1024 GigaByte equals to
a) 1 GigaByte
b) 1 TeraByte
c) 1 YottaByte
d) None of these
Answer:
b) 1 TeraByte

Question 19.
1 MB equals to ________ bytes.
a) 2¹⁰
b) 2²⁰
c) 2³⁰
d) 2⁴⁰
Answer:
b) 2²⁰

Question 20.
What is the decimal value of 1111₂?
(a) 10
(b) 11
(c) 14
(d) 15
Answer:
(d) 15

Question 21.
1 TB equals to_______ bytes
a) 2¹⁰
b) 2²⁰
c) 2³⁰
d) 2⁴⁰
Answer:
d) 2⁴⁰

Question 22.
The decimal value of Binary number 10 is ………………..
(a) 101010
(b) 2
(c) 100
(d) A
Answer:
(b) 2

Question 23.
1 ExaByte (1EB) equals to _________ bytes
a) 2⁵⁰
b) 2⁶⁰
c) 2⁷⁰
d) 2⁸⁰
Answer:
b) 2⁶⁰

Question 24.
Which of the following are data?
(a) Alphabet
(b) Special character
(c) Number
(d) All of these
Answer:
(d) All of these

Question 25.
1 YottaByte equals to_________ bytes.
a) 2⁵⁰
b) 2⁶⁰
c) 2⁷⁰
d) 2⁸⁰
Answer:
d) 2⁸⁰

Question 26.
Pick the odd one.
(a) BCD
(b) ENIAC
(c) ASCII
(d) EBCDIC
Answer:
(b) ENIAC

Question 27.
________are used to represent characters in a text.
a) Bytes
b) Bits
c) Nibbles
d) None of these
Answer:
a) Bytes

Question 28.
Unicode can handles how many characters?
(a) 64
(b) 128
(c) 256
(d) 65536
Answer:
(d) 65536

Question 29.
ASCII is a _________ bit code.
a) 8
b) 7
c) 16
d) 32
Answer:
b) 7

Question 30.
Which one is the rightmost bit?
(a) MSB
(b) LSB
(c) USB
(d) USRB
Answer:
(b) LSB

Question 31.
The ASCII value for Numeric 0(zero) is_______
a) 48
b) 38
c) 128
d) 32
Answer:
a) 48

Question 32.
The leftmost bit of a positive binary number in signed notation is ………………..
(a) 0
(b) 1
(c) 2
(d) A
Answer:
(a) 0

Question 33.
Each number system is uniquely identified by its _________
a) base value
b) radix
c) base value or radix
d) symbols
Answer:
c) base value or radix

Question 34.
The radix for the octal number system is ………………..
(a) 2
(b) 8
(c) 1
(d) 16
Answer:
(b) 8

Question 35.
_________is the general idea behind positional numbering system.
a) base value
b) radix
c) base or radix
d) symbols
Answer:
c) base or radix

Question 36.
Which one of the following companies have formulated EBCDIC?
(a) Microsoft
(b) 1 BM
(c) Sun
(d) Apple
Answer:
(b) 1 BM

Question 37.
The leftmost bit in the binary number is called the _________
a) MSB
b) LSB
c) FSB
d) None of these
Answer:
a) MSB

Question 38.
The base value of a hexadecimal number is ………………..
(a) 2
(b) 8
(c) 16
(d) 18
Answer:
(c) 16

Question 39.
Each octal digit has its own positional value or weight as a power of _________
a) 8
b) 16
c) 4
d) 10
Answer:
a) 8

Question 40.
How many truth values are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(a) 2

Question 41.
_______system is used to represent data in a more compact manner.
a) Hexadecimal
b) Octal
c) Decimal
d) None of these
Answer:
a) Hexadecimal

Question 42.
The variables which can store the truth values are called………………..
(a) logical variable
(b) binary-valued variable
(c) boolean variables
(d) all of these
Answer:
(d) all of these

Question 43.
How many methods are there to convert decimal numbers to binary numbers?
a) only one
b) 2
c) 3
d) many
Answer:
b) 2

Question 44.
Which is not a logical operator?
(a) dot
(b) plus
(c) over bar
(d) command
Answer:
(d) command

Question 45.
Computer can handle _______numbers.
a) positive
b) negative
c) positive and negative
d) None of these
Answer:
c) positive and negative

Question 46.
Which symbol is used in the OR operator?
(a) –
(b) •
(c) *
(d) +
Answer:
(d) +

Question 47.
The simplest method to represent negative binary numbers is called_______method.
a) 1’s complement
b) 2’s complement
c) signed magnitude
d) All the above
Answer:
c) signed magnitude

Question 48.
Which among the following can be replaced by a bubbled AND gate?
(a) AND
(b) NAND
(c) OR
(d) not
Answer:
(b) NAND

Question 49.
How many ways a number can be represented in computers?
a) 3
b) 2
c) only one
d) None of these
Answer:
a) 3

Question 50.
Find the universal gates from the following.
(a) XOR
(b) XNOR
(c) a and b
(d) NOR
Answer:
(d) NOR

Question 51.
If the number has _______sign, it will be considered as positive in signed magnitude representation.
a) +
b) no
c) + or ++
d) A or B
Answer:
d) A or B

Question 52.
Which symbol is used in the XOR gate?
(a) \(\odot\)
(b) \(\otimes\)
(c) \(\oplus\)
(d) –
Answer:
(c) \(\oplus\)

Question 53.
Included dot means ………………..
(a) \(\odot\)
(b) [•]


Answer:
(a) \(\odot\)

Question 53.
1’s complement of (00011000)2 is _______
a) 11100111
b) 00011001
c) 00000011
d) None of these
Answer:
a) 11100111

Question 55.
Identify the statement which is wrong.
(a) A . 1 = A
(b) A . A = A
(c) A + O = A
(d) A . 1 = 0
Answer:
(b) A . A = A

Question 55.
The binary numbers permits _______ computation.
a) addition and subtraction
b) multiplication
c) division
d) all the above
Answer:
d) all the above

Question 57.
Identify the statements which are true.
(i) A + 0 = A
(ii) A.A = A
(iii) A + \(\overline{\mathrm{A}}\) = 1
(iv) A. O = O

(a) (iii) (iv) are true
(b) (i) (ii) are true
(c) (i) (ii) (iii) are true.
(d) all are true
Answer:
(d) all are true

Question 58.
All the characters in the character set are denoted through_______only.
a) numbers
b) alphanumeric
c) alphabet
d) None of these
Answer:
a) numbers

Question 59.
Match the following

(a) 3 4 2 1
(b) 1 2 3 4
(c) 4 3 2 1
(d) 3 4 1 2
Answer:
(a) 3 4 2 1

Question 60.
BCD stands for _______
a) Binary Coded Decimal
b) Binary Character Decoding
c) Basic Coded Decimal
d) Bit Coded Decimal
Answer:
a) Binary Coded Decimal

PART – 2
II. Short Answers

Question 1.
Define data.
Answer:
Data is an unprocessed collection of facts given as input to the computer. In a program, the values assigned to the variables are called data.

Question 2.
Expand ASCII.
Answer:
American Standard Code for Information Interchange

Question 3.
What do you mean by nibble?
Answer:
A nibble is a collection of 4 bits binary digits.

Question 4.
What is MSB and LSB?
Answer:
MSB means Most Significant Bit; LSB-Least Significant Bit

Question 5.
What do you mean by word length?
Answer:
Word length refers to the number of bits processed by a Computer’s CPU. For example, a word length can have 8 bits, 16 bits, 32 bits, and 64 bits.

Question 6.
Define word length?
Answer:
Word length refers to the number of bits processed by a computer’s CPU.

Question 7.
Write note on number system.
Answer:
A numbering system is a way of representing numbers. The most commonly used numbering system in real life is the Decimal number system. Other number systems are Binary, Octal, and Hexadecimal Number System.

Question 8.
How will you convert a number from octal to Binary?
Answer:
For each octal digit in the given number write its 3 digits binary equivalent using positional notation.

Question 9.
Why the computers are working at different speeds?
Answer:
The speed of a computer depends on the number of bits it can process at once. For example, a 64- bit computer can process 64-bit numbers in one operation, while a 32-bit computer breaks 64- bit numbers down into smaller pieces, making it slower.

Question 10.
Write a short note on BCD.
Answer:

1. BCD stands for Binary Coded Decimal system.
2. BCD is a 26-bit encoding system.
3. IT can handle 64 characters.

PART – 3
III. Explain in Brief

Question 1.
What is a binary number system?
Answer:
There are only two digits in the Binary system, namely, 0 and 1. The numbers in the binary system are represented to the base 2 and the positional multipliers are the powers of 2. The leftmost bit in the binary number is called as the Most Significant Bit (MSB) and it has the largest positional weight. The rightmost bit is the Least Significant Bit (LSB) and has the smallest positional weight.

Example:
The binary sequence (11101)₂ has the decimal equivalent:
(1101)₂ = 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2⁰
= 8 + 4 + 0 + 1
= (13)₁₀

Question 2.
Explain the Hexadecimal number system.
Answer:
A hexadecimal number is represented using base 16. Hexadecimal or Hex numbers are used as a shorthand form of a binary sequence. This system is used to represent data in a more compact manner. Since 16 symbols are used, 0 to F, the notation is called hexadecimal.

The first 10 symbols are the same as in the decimal system, 0 to 9, and the remaining 6 symbols are taken from the first 6 letters of the alphabet sequence, A to F, where A represents 10, B is 11, C is 12, D is 13, E is 14 and F is 15.

Question 3.
What is a decimal number system?
Answer:
It consists of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9(10 digits). It is the oldest and most popular number system used in our day to day life. In the positional number system, each decimal digit is weighted relative to its position in the number. This means that each digit in the number is multiplied by 10 raised to a power corresponding to that digit’s position.
Example:
(123)₁₀ = (1 x 10²) + (2 x 10¹) + (3 x 10⁰)
= 100 + 20 + 3
= (123)₁₀

Question 4.
Write the distributive law.
Answer:
A . (B + C) = A . B + A . C
A + (B . C) = (A + B) . (A + C)

Question 5.
What is the truth table?
Answer:
A truth table represents all the possible values of logical variables or statements along with all the possible results of a given combination of truth values.

PART – 4
IV. Explain in Detail

Question 1.
Explain the different types of number systems?
Answer:
Different Types of Number Systems

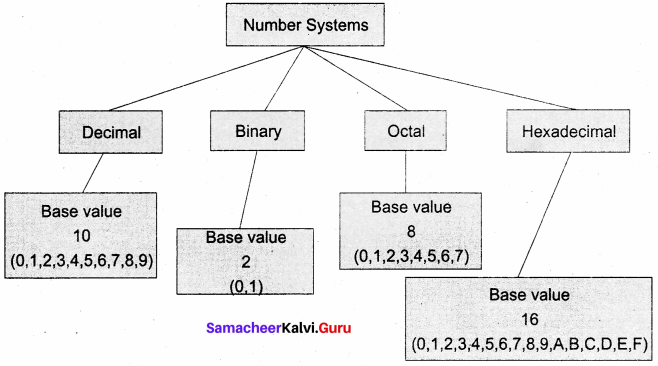
A numbering system is a way of representing numbers. The most commonly used numbering system in real life is the Decimal number system. Other number systems are the Binary, Octal, Hexadecimal number systems. Each number system is uniquely identified by its base value or radix. Radix or base is the count of a number of digits in each number system. Radix or base is the general idea behind the positional numbering system.

Decimal Number System:
It consists of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9(10 digits). It is the oldest and most popular number system used in our day-to-day life. In the positional number system, each decimal digit is weighted relative to its position in the number. This means that each digit in the number is multiplied by 10 raised to a power corresponding to that digit’s position.
Example:
(123)₁₀ = 1 x 10² + 2 x 10¹ + 3 x 10⁰
= 100 + 20 + 3
= (123)₁₀

Binary Number System:
There are only two digits in the Binary system, namely, 0 and 1. The numbers in the binary system are represented to the base 2 and the positional multipliers are the powers of 2. The leftmost bit in the binary number is called the Most Significant Bit (MSB) and it has the largest positional weight. The rightmost bit is the Least Significant Bit (LSB) and has the smallest positional weight.

Example:
The binary sequence (1101)₂ has the decimal equivalent:
(1101)₂ = 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2⁰
= 8 + 4 + 0 + 1
= (13)₁₀

Octal Number System:
Octal number system uses digits 0,1,2,3,4,5,6 and 7 (8 digits). Each octal digit has its own positional value or weight as a power of 8.
Example:
The Octal sequence (547)₈ has the decimal equivalent:
(547)₈ = 5 x 8² + 4 x 8² + 7 x 8⁰
= 5 x 64 + 4 x 8 + 7 x 1
= 320 + 32 + 7
= (359)₁₀

Hexadecimal Number System:
A hexadecimal number is represented using base 16. Hexadecimal or Hex numbers are used as a shorthand form of a binary sequence. This system is used to represent data in a more compact manner. Since 16 symbols are used, 0 to F, the notation is called hexadecimal. The first 10 symbols are the same as in the decimal system, 0 to 9, and the remaining 6 symbols are taken from the first 6 letters of the alphabet sequence, A to F, where A represents 10, B is 11, C is 12, D is 13, E is 14 and F is 15.

Question 2.
Explain the octal to decimal conversion and hexadecimal to decimal conversion.
Answer:
Octal to Decimal Conversion:
To convert Octal to Decimal, we can use the positional notation method.

1. Write down the Octal digits and list the powers of 8 from right to left(Positional Notation).
2. For each positional notation of the digit write the equivalent weight.
3. Multiply each digit with its corresponding weight.
4. Add all the values.

Example:
Convert (1265)₈ to an equivalent Decimal number

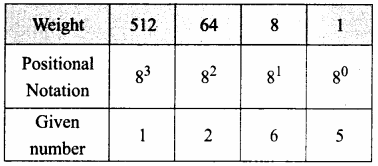
(1265)₈ = 512 x 1 + 64 x 2 + 8 x 6 + 1 x 5
= 512 + 128 + 48 + 5
(1265)₈ = (693)₁₀

Hexadecimal to Decimal Conversion:
To convert Hexadecimal to Decimal we can use the positional notation method.

1. Write down the Hexadecimal digits and list the powers of 16 from right to left (Positional Notation).
2. For each positional notation written for the digit, now write the equivalent weight.
3. Multiply each digit with its corresponding weight.
4. Add all the values to get one final value.

Example:
Convert (25F)₁₆ into its equivalent Decimal number.

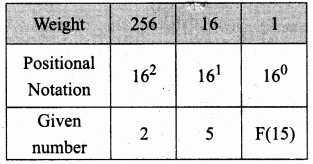
Question 3.
Explain the binary addition and binary subtraction
Answer:
Binary Addition:
The following table is useful when adding two binary numbers.

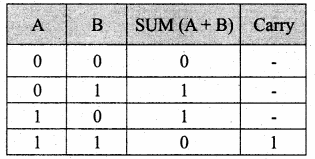
Example Add: 1011₂ + 1001₂

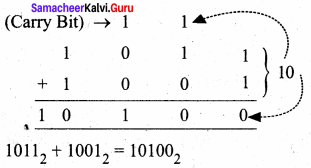
Example: Perform Binary addition for the following:
23₁₀ + 12₁₀
Step 1: Convert 23 and 12 into binary form

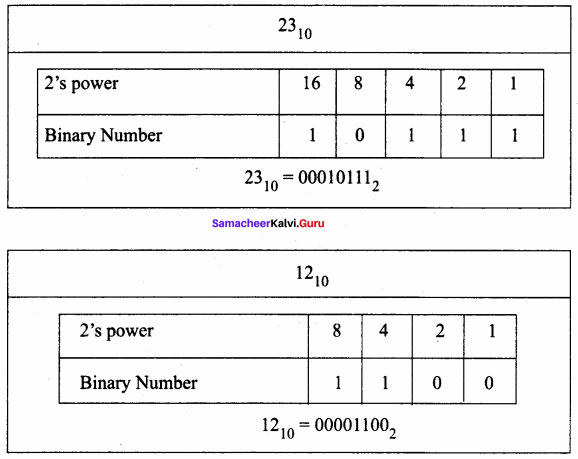
Step 2: Binary addition of 23 and 12:

Binary Subtraction:
The table for Binary Subtraction is as follows:

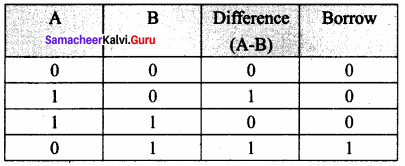
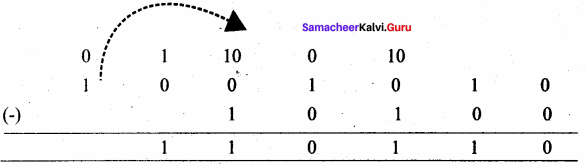
When subtracting 1 from 0, borrow 1 from the next Most Significant Bit, when borrowing from the next Most Significant Bit, if it is 1, replace it with 0. If the next Most Significant Bit is 0, you must borrow from a more significant bit that contains 1 and replace it with 0, and 0s upto that point become 1’s.
Example: Subtract 1001010₂ – 10100₂

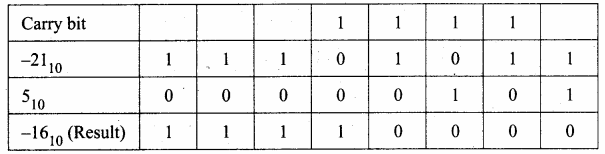
Example Perform binary addition for the following: (-21)₁₀ + (5)₁₀
Step 1: Change – 21 and 5 into binary form

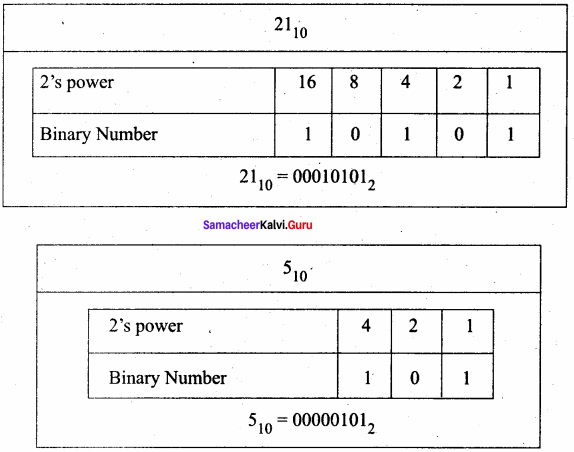
Step 2:

Step 3:
Binary Addition of – 21 and 5:

Question 4.
Explain the theorems of boolean algebra.
Answer:
Theorems of Boolean Algebra:
Identity:
A + 0 = A
A. 1 = A

Complement:
A + \(\overline{\mathrm{A}}\) = 1
A. \(\overline{\mathrm{A}}\) = 0

Commutative:
A + B = B + A
A. B = B .A

Associative:
A + (B + C) = (A + B) + C
A. (B . C) = (A. B). C

Distributive
A. (B + C) = A B + A. C
A + (B . C) = (A + B). (A + C)

Null Element:
A + 1 = 1
A. 0 = 0

Involution
(\(\overset { = }{ A }\)) = A

Indempotence:
A +A = A
A.A = A

Absorption:
A + (A . B) = A
A . (A + B) = A

3rd Distributive:
A + \(\overline{\mathrm{A}}\). B = A + B

De Morgan’s:
\(\overline{\mathrm{A+B}}\) = \(\overline{\mathrm{A}}\).\(\overline{\mathrm{B}}\)
(\(\overline{\mathrm{A.B}}\)) = \(\overline{\mathrm{A}}\) + \(\overline{\mathrm{B}}\)