Samacheer Kalvi 11th Economics Solutions Chapter 12 Mathematical Methods for Economics

Guys who are planning to learn the fundamentals of Economics Solutions can avail the handy study material Samacheer Kalvi Class 11th Economics Solutions Chapter 12 Mathematical Methods for Economics Questions and Answers here. Refer to the Samacheer Kalvi Economics Solutions for Class 11th PDF available and score better grades. Simply click on the quick links available for Samacheer Kalvi 11th Economics Solutions Chapter 12 Mathematical Methods for Economics and prepare all the concepts in it effectively. Take your preparation to the next level by availing the Tamilnadu State Board Solutions for Class 11th Economics Solutions Chapter 12 Mathematical Methods for Economics prepared by subject experts.

Tamilnadu Samacheer Kalvi 11th Economics Solutions Chapter 12 Mathematical Methods for Economics

Do you feel the concept of Economics Solutions difficult to understand? Not anymore with our Samacheer Kalvi for Class 11th Economics Solutions Chapter 12 Mathematical Methods for Economics Questions and Answers. All the Solutions are given to you with detailed explanation and you can enhance your subject knowledge. Use the Samacheer Kalvi Textbook Chapter 12 Mathematical Methods for Economics Solutions PDF free of cost and prepare whenever you want.

Samacheer Kalvi 11th Economics Mathematical Methods for Economic Text Book Back Questions and Answers

Part – A
Multiple Choice Questions

Question 1.
Mathematical Economics is the integration of ____________
(a) Mathematics and Economics
(b) Economics and Statistics
(c) Economics and Equations
(d) Graphs and Economics
Answer:
(a) Mathematics and Economics

Question 2.
The construction of demand line or supply line is the result of using ____________
(a) Matrices
(b) Calculus
(c) Algebra
(d) Analytical Geometry
Answer:
(d) Analytical Geometry

Question 3.
The first person used the mathematics in Economics is ____________
(a) Sir William Petty
(b) Giovanni Ceva
(c) Adam Smith
(d) Irving Fisher
Answer:
(a) Sir William Petty

Question 4.
Function with single independent variable is known as ____________
(a) Multivariate Function
(b) Bivariate Function
(c) Univariate Function
(d) Polvnomial Function
Answer:
(c) Univariate Function

Question 5.
A statement of equality between two quantities is called ____________
(a) Inequality
(b) Equality
(c) Equations
(d) Functions
Answer:
(c) Equations

Question 6.
An incremental change in dependent variable with respect to change in independent variable is known as ____________
(a) Slope
(b) Intercept
(c) Variant
(d) Constant
Answer:
(a) Slope

Question 7.
(y – y₁) = m (x – x₁) gives the ____________
(a) Slope
(b) Straight line
(c) Constant
(d) Curve
Answer:
(b) Straight line

Question 8.
Suppose D = 50 – 5P. When D is zero then ____________
(a) P is 10
(b) P is 20
(c) P is 5
(d) Pis-10
Answer:
(a) Pis 10

Question 9.
Suppose D = 150 – 50P. Then, the slope is
(a) -5
(b) 50
(c) 5
(d) – 50
Answer:
(d) – 50

Question 10.
Suppose determinant of a matrix A = 0, then the solution ____________
(a) Exists
(b) Does not exist
(c) Is infinity
(d) Is zero
Answer:
(b) Does not exist

Question 11.
State of rest is a point termed as ____________
(a) Equilibrium
(b) Non – Equilibrium
(c) Minimum Point
(d) Maximum Point
Answer:
(a) Equilibrium

Question 12.
Differentiation of constant term gives ____________
(a) one
(b) zero
(c) infinity
(d) non – infinity
Answer:
(b) zero

Question 13.
Differentiation of xⁿ is ____________
(a) nx ^{(n – 1)}
(b) nx ^{(n + 1)}
(c) zero
(d) one
Answer:
(a) nx ^{(n – 1)}

Question 14.
Fixed Cost is the ____________ term in cost function represented in mathematical form.
(a) Middle
(b) Price
(c) Quantity
(d) Constant
Answer:
(d) Constant

Question 15.
The first differentiation of Total Revenue function gives ____________
(a) Average Revenue
(b) Profit
(c) Marginal Revenue
(d) Zero
Answer:
(c) Marginal Revenue

Question 16.
The elasticity of demand is the ratio of ____________
(a) Marginal demand function and Revenue function
(b) Marginal demand function to Average demand function
(c) Fixed and variable revenues
(d) Marginal Demand function and Total demand function
Answer:
(b) Marginal demand function to Average demand function

Question 17.
If x + y = 5 and x – y = 3 then, Value of x ____________
(a) 4
(b) 3
(c) 16
(d) 8
Answer:
(a) 4

Question 18.
Integration is the reverse process of
(a) Difference
(b) Mixing
(c) Amalgamation
(d) Differentiation
Answer:
(d) Differentiation

Question 19.
Data processing is done by ____________
(a) PC alone
(b) Calculator alone
(c) Both PC and Calculator
(d) Pen drive
Answer:
(c) Both PC and Calculator

Question 20.
The command Ctrl + M is applied for ____________
(a) Saving
(b) Copying
(c) getting new slide
(d) deleting a slide
Answer:
(c) getting new slide

Part – B
Answer the following questions in one or two sentences

Question 21.
If 62 = 34 + 4x  what is x?
solution:
If 62 = 34 + 4x what is x
Given:
62 = 34 + 4x
34 + 4x = 62
4x = 62-34
4x = 28
x = \(\frac { 28 }{ 4 }\)
x = 7

Question 22.
Given the demand function q = 150 – 3p, derive a function for MR.
Solution:
Given:
q = 150 – 3p
\(\frac { dq }{ dq }\) = 0 – 3 (1)
\(\frac { dq }{ dq }\) = – 3
Revenue = price × quantity = p (150 – 3p)
= p (150 – 3p)
= 150p – 3p²
MR = \(\frac { dq }{ dq }\) = 150 \(\frac { dq }{ dq }\) -6p \(\frac { dq }{ dq }\)
= 150 (\(\frac { – 1 }{ 3 }\)) – 6p (\(\frac { – 1 }{ 3 }\))
= – 50 + 2p
= – 50 = 2 (\(\frac { 150 – q }{ 3 }\))
= 50 + 100 + \(\frac { – 2 q }{ 3 }\)
= 50 – \(\frac { 2 q }{ 3 }\)
= 50 – \(\frac { 2 }{ 3 }\) (150 – 3p)
MR = 2p – 50

Question 23.
Find the average cost function where TC = 60 + 10x +15x²
Solution:
Given:
TC = 60 + 10x +15x²
Average Cost = \(\frac { TC }{ x }\)
= \(\frac{60+10 x+15 x^{2}}{x}\)
= \(\frac { 60 }{ x }\) + \(\frac { 10x }{ x }\) + \(\frac{15 x^{2}}{x}\)
AC = \(\frac { 60 }{ x }\) + 10 + 15x

Question 24.
The demand function is given by x = 20 – 2p – p² where p and x are the price and the quantity respectively. Find the elasticity of demand for p = 2.5.
Solution:
Given:
x = 20 – 2p – p²
p = 2.5
e_d = (\(\frac { p }{ x }\)) (\(\frac { dx }{ dp }\))
If p = 2.5 then x,
x = 20 – 2 (2.5) – (2.5)²
= 20 – 5 – (6.25)
= 15 – 6.25
x = 8.75
Here x = 20 – 2p – p²
\(\frac { dx }{ dp }\) = 0 – 2 (1) – 2p
= -2 – 2p
If P = 2.5 then
\(\frac { dx }{ dp }\) = -2 – 2 (2.5)
= -2 – 5
\(\frac { dx }{ dp }\) = – 7
e_d = \(\frac { -2.5 }{ 8.75 }\) × – 7
= 0.2857 × – 7
e_d = 2

Question 25.
Suppose the price p and quantity q of a commodity are related by the equation q = 30 – 4p – p²
find :

1. e_d at p = 2
2. MR

Solution:
Given:
q = 30 – 4p – p²
1. e_d = (\(\frac { p }{ x }\))(\(\frac { dx }{ dp }\))
If P = 2 then
x = 30 – 4 (2) – 2²
= 30 – 8 – 4
=20 – 12
x = 18
\(\frac { dx }{ dp }\) =30 – 4p – p²
= 0 – 4 – 2p
= 0 – 4 – 2 (2)
= -4 -4
= -8
e_d = \(\frac { 2 }{ 18 }\) (-8)
x = – \(\frac { 16 }{ 18 }\)
e_d = – 0.88

2. MR
TR = p ×q
TR = p (30 – 4p – p²)
= 30p – 4p² – p³
MR = \(\frac { d(TR) }{ dp }\)
= 30 – 8p – 3p²
If p = 2
MR = 30 – 8 (2) – 3 (2)²
= 30 – 16 12
MR = 2

Question 26.
What is the formula for elasticity of supply if you know the supply function?
Solution:
Elasticity of supply = (\(\frac { p }{ q }\)) (\(\frac { dq }{ dp }\))

Question 27.
What are the Main menus of MS Word?
Answer:

1. Home menu
2. Insert
3. Page layout
4. Reference
5. Review
6. View
7. Print layout
8. Outline
9. Task pane
10. Tool bars
11. Header and footer
12. Foot notes

Part – C
Answer the following questions in one Paragraph

Question 28.
Illustrate the uses of Mathematical Methods in Economics.
Answer:

1. Mathematical methods help to present the economic problems in a more precise form.
2. Mathematical methods help to explain economic concepts.
3. Mathematical methods help to use a large number of variables in economic analyses.
4. Mathematical methods help to quantify the impact or effect of any economic activity implemented by government or anybody.

Question 29.
Solve for A: quantity demanded if 16x – 4 = 68 + 7x.
Solution:
Given:
16x  – 4 = 68 + 1x
16x – 7x = 68 + 4
9x = 72
x = (\(\frac { 72 }{ 9 }\))
x = 8

Question 30.
A firm has the revenue function R = 600q – 0.03q² and the cost function is C = 150q + 60,000, where q is the number of units produced. Find AR, AC, MR and MC.
Solution:
Given:
R = 600q – 0.03q²
C = 150q + 60000

(i) AR = \(\frac { R }{ q }\)
= \(\frac{600 q-0.03 q^{2}}{q}\)
= \(\frac { 600q }{ q }\) – \(\frac{0.03 \mathrm{q}^{2}}{\mathrm{q}}\)
= AR = 600 – 0.0.q

(ii) AC = \(\frac { c }{ q }\)
= \(\frac { 150q + 60000 }{ q }\)
= \(\frac { 150q }{ q }\) + \(\frac { 60000 }{ q }\)
AC = 150 + (\(\frac { 60000 }{ q }\))

(iii) MR = \(\frac { dr }{ dq }\)
R = 600q – 0.03q
\(\frac { dR }{ dq }\) = 600 (1) – 0.03 (2q)
MR = 600 – 0.06q

(iv) MC = \(\frac { dc }{ dq }\)
C = 150q + 60000
\(\frac { dc }{ dq }\) = 150 (1) + 0
MC = 150

Question 31.
Solve the following linear equations by using Cramer’s rule.
x₁ – x₂ + x₃ = 2
– x₁ – x₂ – x₃ = 0
– x₁ – x₂ – x₃ = – 6
Solution:

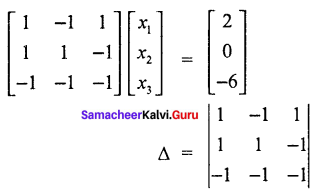
= 1 (- 1 – 1) + 1 (- 1 – 1) + 1 (- 1 + 1)
= 1(- 2) + 1 (0)
∆ = – 2 – 2
∆ = – 2 – 2
∆ = – 4

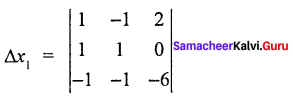
= 2 (- 1 – 1) + 1 (0 + 6) + 1 (0 – 6)
= 2 (- 2) + 1(6) + 1 (- 6)
= – 4 + 6 – 6
∆ = – 4

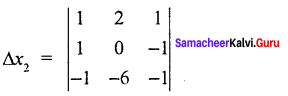
= 1 (0 – 6) – 2 (- 1 – 1)+1(- 6 + 0)
= 1 (- 6) – 2 (- 2) + 1 (- 6)
= – 6 + 4 – 6
= – 12 + 4
∆x₃ = -8

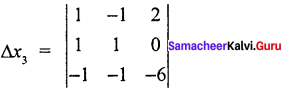
1 (- 6 + 0) + 1 (- 6 + 0) + 2 (- 1 + 1)
= 1 (- 6) + 1 (- 6) + 2 (0)
= – 6 – 6
∆x₃ = – 12

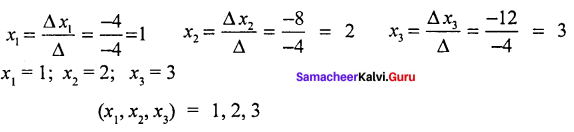
Question 32.
If a firm faces the total cost function TC = 5+ x² where x is output, what is TC when x is 10?
Solution:
Given:
TC = 5 + x²
If x = 10
TC = 5 + 10²
= 5 + 100
TC = 105

Question 33.
If TC = 2.5q³ – 13q² + 50q + 12 derive the MC function and AC function.
solution:
Given:
TC= 2.5q³ – 13q² + 50q + 12
Marginal cost function
MC = \(\frac { d(TC) }{ dQ }\)
= \(\frac { d }{ dq }\) [2.5q³ – 13q² + 50q + 12]
= 2.5 (3q²) – 13 (2q) + 50 (1) + 0
MC = 7.5q – 26q + 50
Average cost AC =\(\frac { TC }{ q }\)
= \(\frac{2.5 q^{3}-13 q^{2}+50 q+12}{q}\)
= \(\frac{2.5 q^{3}}{q}\) – \(\frac{13 q^{2}}{q}\) + \(\frac { 50q }{ q }\) + \(\frac { 12 }{ q }\)
AC = 2.5q – 13q + 50 + \(\frac { 12 }{ q }\)

Question 34.
What are the steps involved in executing a MS Excel Sheet?
Answer:
MS excel is used in data analysis by using formula. A spread sheet is a large sheet of paper which contains rows and columns.
To start a excel there are various options.
Click Start → Program → Microsoft Excel
Double click the MS Excel Icon from the Desktop.

Part – D
Answer the following questions in about a page

Question 35.
A Research scholar researching the market for fresh cow milk assumes that Qt = f (Pt, Y, A, N, Pc) where Qt is the quantity of milk demanded, Pt is the price of fresh cow milk, Y is average household income, A is advertising expenditure on processed pocket milk, N is population and Pc is the price of processed pocket milk.

1. What does Qt= f (Pt, Y,A,N, Pc) mean in words?
2. Identify the independent variables.
3. Make up a specific form for this function. (Use your knowledge of Economics to deduce whether the coefficients of the different independent variables should be positive or negative.)

Solution:
1. Qt is the function of Pt, Y, A, N, Pc
The determinants of demand are
Pt = Price of fresh cow milk.
Y = Average household income
A = Advertising expenditure on processed pocket milk
N = Population
Pc = Price of processed pocket milk.

2. Y and N are independent variables

3. Average household income and population are directly proportional to quantity demanded of cow’s milk (ie if Y and N increases Qt also increase)
Price of fresh cow milk, advertising expenditure on pocket milk and price of processed pocket milk are inversely proportional to Qt.
There
Qt = – aPt + by – CA + dN – ePc

Question 36.
Calculate the elasticity of demand for the demand schedule by using differential calculus method P = 60 – 0.2 Q where price is

1. zero
2. Rs.20
3. Rs.40

Solution:
P = 60 – 0.2 Q
0.2 Q = 60 – P
(0.2 Q) 10 = (60 – p) 10
2 Q = 600 – 10p
Q = 300 – 5p
Given demand function Q = 300 – 5p
1. If P = 0 then Q = 300 – 5 (0)
= 300
\(\frac { dq }{ dp }\) = 300 – 5p
= 0 – 5
\(\frac { dq }{ dp }\) = – 5
e_d = \(\frac { p }{ p }\)(\(\frac { dq }{ dp }\))
= \(\frac { 0 }{ 300 }\)(-5)
e_d = 0

2. If p = 20 then Q = 300 = 5 (20)
= 200
e_d = \(\frac { 20 }{ 200 }\) (-5)
= – \(\frac { 100 }{ 200 }\)
e_d = – 0.5

3. If = 40 then Q = 300 – 5 (40)
= 300 – 200
Q = 100
e_d = \(\frac { p }{ q }\)(\(\frac { dq }{ dp }\))
= \(\frac { 40 }{ 100 }\) (-5)
e_d = – \(\frac { 200 }{ 100 }\)
e_d = -2

Question 37.
The demand and supply functions are pd=1600 – x² and ps = 2x² + 400 respectively. Find the consumer’s surplus and producer’s surplus at equilibrium point.
Answer:
At equilibrium p_d = p_s
1600 – x² = 2x² + 400
– x² – 2x² = 400 – 1600
– 3x² = – 1200
x² = \(\frac { 1200 }{ 3 }\)
x² = 400
x = 20
If x = 20 p_o = 1600 – (20)²
= 1600 – 400
p_o = 1200
p_o x_o = 1200 × 20
= 24000

= 8000 – \(\frac { 8000 }{ 3 }\)
= \(\frac { 24000 – 8000 }{ 3 }\)
= \(\frac { 16000 }{ 3 }\)
C.S = 5333.3

Question 4.
What are the ideas of information and communication technology used in economics?
Answer:
Information and Communication Technology (ICT) is the infrastructure that enables computing faster and accurate

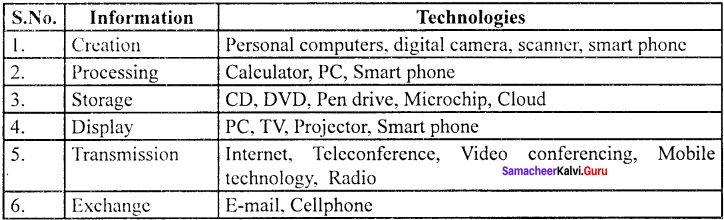
In economics the uses of mathematical and statistical tools need the support of ICT for data compiling, editing, manipulating and presenting the results.

Samacheer Kalvi 11th Economics Introduction To Micro-Economics Additional Questions and Answers

Match the following and choose the answer using the codes given below

Question 1.

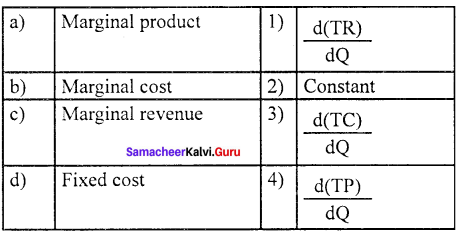
(a) 1 2 3 4
(b) 2 3 4 1
(c) 3 4 2 1
(d) 4 3 1 2
Answer:
(c) 3 4 2 1

Question 2.

(a) 4 3 1 2
(b) 2 3 4 1
(c) 1 2 3 4
(d) 3 2 1 4
Answer:
(a) 4 3 1 2

Question 3.

(a) 1 2 3 4
(b) 3 4 1 2
(c) 4 3 1 2
(d) 2 3 4 1
Answer:
(b) 3 4 1 2

Choose the incorrect statement

Question 4.
(a) Differentiation of constant is zero
(b) Differentiation of xn is x
(c) Constant value is known as fixed cost
(d) x° = 1 when x = 0
Answer:
(d) x° = 1 when x = 0

Question 5.
(a) The population density of T.N is 480 as per 2011 census.
(b) There are 30 national highways in Tamil Nadu.
(c) Tamil Nadu has the highest installed wind energy capacity in India.
(d) The headquarters of southern railway is at Trichy
Answer:
(b) There are 30 national highways in Tamil Nadu.

Pick the odd one out

Question 6.
(a) Arithmetic
(b) Comparison
(c) Text concatenation
(d) Foot note
Answer:
(d) Foot note

Question 7.
(a) X = independent variable
(b) Y = dependent variable
(c) X = f (y)
(d) M – slope
Answer:
(c) X = f (y)

Choose the correct statement

Question 8.
(a) X + Y = 6 and X – Y = 2 then X = 4
(b) If D = 60 – 6P when D is 0 then P is 20
(c) In the equation 0.1 X² + 1 OX + 100 constant = 10
(d) If Y = 6X³ then slope is 9X:
Answer:
(a) X + Y = 6 and X – Y = 2 then X = 4

Choose the incorrect pair

Question 9.

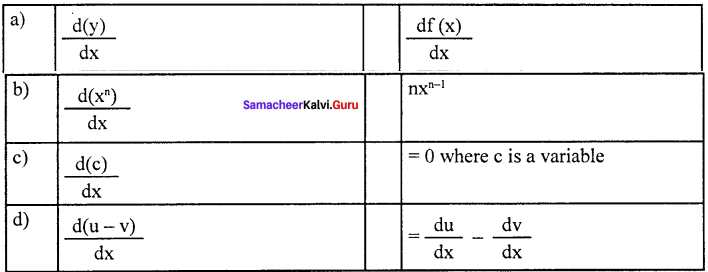
Answer:
(c) \(\frac { d(c) }{ dx }\) = 0 where c is a variable

Question 10.

Answer:
(a) ∫f(x) dx – (i) F (x) + C

Fill in the blanks with suitable option given below

Question 11.
__________ is the first to use mathematics in economics.
(a) Giovanni Ceva
(b) William petty
(c) J.M.Keynes
(d) None
Answer:
(b) William petty

Question 12.
The formula for constructing a straight line is __________
(a) \(\mathrm{m}=\frac{\mathrm{y}_{2}-\mathrm{y}_{1}}{\mathrm{x}_{2}-\mathrm{x}_{1}}\)
(b) y = mx
(c) \(\frac { Change in x }{ Change in y }\)
(d) (y -y₁) = m (x – x₁)
Answer:
(d) (y -y₁) = m (x – x₁)

Question 13.
If the determinant ∆ = ?, then solution does not exist
(a) 1
(b) 0
(c) 2
(d) -1
Answer:
(b) 0

Question 14.
Power rule ∫xdx ______
(a) \(\frac{x^{2}}{n+1}\) + C
(b) \(\frac { pq }{ n + 1 }\) + C
(c) \(\frac{\mathrm{x}^{(\mathrm{n}+1)}}{\mathrm{n}+1}\) + C
(d) None
Answer:
(c) \(\frac{\mathrm{x}^{(\mathrm{n}+1)}}{\mathrm{n}+1}\) + C

Question 15.
______ is a rectangular array of numbers systematically arranged in rows and columns within brackets.
(a) Matrix
(b) Determinants
(c) Function
(d) None
Answer:
(a) Matrix

Choose the best option

Question 16.
__________ provides the solution of a system of linear equations with ‘n’ variables and ‘n’ equations
(a) Demand function
(b) Consumer’s surplus
(c) Equilibrium
(d) Cramer’s rule
Answer:
(d) Cramer’s rule

Question 17.
The first known writer to apply mathematical method to economic problems was __________
(a) Giovanni ceva
(b) William petty
(c) Keynes
(d) None
Answer:
(a) Giovanni ceva

Question 18.
In y = f (x) which is the independent variable
(a) f
(b) y
(c) x
(d) None
Answer:
(c) x

Question 19.
Formula for marginal cost is
(a) MC = \(\frac { d(TC) }{ dQ }\)
(b) MC = \(\frac { d(TC) }{ dP }\)
(c) MC = \(\frac { d(TC) }{ dQ }\)
(d) None
Answer:
(a) MC = \(\frac { d(TC) }{ dQ }\)

Question 20.
Function with a single independent variable are called _____
(a) Multivariate function
(b) Consumption function
(c) Simple univariate function
(d) None
Answer:
(c) Simple univariate function

Part – B
Answer the following questions in one or two sentences

Question 1.
What is economic analysis?
Answer:
Economic analysis is a systematic approach to determine the optimum use of scare resources and choose available alternatives and select the best alternative to achieve a particular objective.

Question 2.
What is the slope of a straight line ?
Answer:
Slope or gradient of the line represents the ratio of the changes in vertical and horizontal lines

Question 3.
State the phases of evolution of ICT?
Answer:

1. Computer
2. PC
3. Micro Processor
4. Internet and
5. Wireless links.

Question 4.
What are determinants ?
Answer:
The determinant is an arrangement of same elements of the corresponding matrix into rows and columns by enclosing vertical lines.

Question 5.
State the application of differential calculus.
Answer:

1. To find the rate of change in demand with respect to price.
2. To find the rate of change in income with respect to the investment.

Question 6.
What is ICT?
Answer:
Information and Communication Technology (ICT) is the infrastructure that enables computing faster and accurate.

Question 7.
What is a work sheet?
Answer:
A worksheet is a table like document containing rows and columns with data and formula

Part – C
Answer the following questions in one Paragraph

Question 1.
The marginal cost function for producing x units is y = 23 + 16.x – 3.x2 and the total cost for producing zero unit is Rs. 40. Obtain the total cost function and the average cost function.
Solution:
Given Marginal cost functions
y = 23 + 16x – 3x²
C = 40

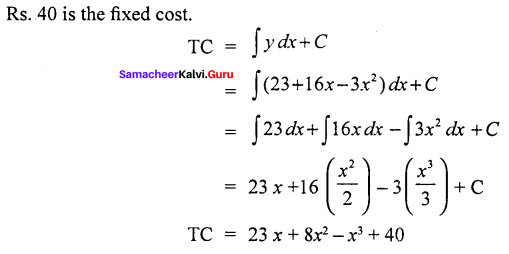
Average cost function = \(\frac { TC }{ x }\)
= \(\frac{23 x+8 x^{2}-x^{3}+40}{x}\)
AC = 23 + 8x – x + \(\frac { 40 }{ x }\)

Question 2.
Find the solution of the system of equations
5x₁ + 3x₂ = 30
6x₁ – 2X₂ = 8
Solution :

Question 3.
If the demand function is p = 35 – 2x – x² and the demand x_o is 3, what will be the consmer’s surplus
Solution:
Given:
p = 35 – 2x – x²
If x = 3 then
p = 35-2 (3) – 3²
= 35 – 6 – 9
p = 20

= 35 (3) – 9 – 9 – 60
= 105 – 9 – 9 – 60
CS = 27 units

Question 4.
Given the total cost function TC = 15 + 3Q2 + 7Q3 drive the marginal cost function.
Solution:
Given:
TC = 15 + 3Q² + 7Q²
MC = \(\frac { d(15) }{ dQ }\) + \(\frac{\mathrm{d}\left(3 \mathrm{Q}^{2}\right)}{\mathrm{d} \mathrm{Q}}\) + \(\frac{\mathrm{d}\left(7 \mathrm{Q}^{3}\right)}{\mathrm{d} \mathrm{Q}}\)
= 0+ 3 (2) Q + 7 (3) Q + (3) Q²
MC = 6Q + 21 Q²

Question 5.
Find the value of the determinant of the matrix
Solution:
Given:

= 3 (-5) -4 (-19) +7 (-3)
= -15 + 76 – 21
A = 40

Question 6.
Find the value of the determinant of the matrix A =.
Solution:
Given:

Part – D
Answer the following questions in about a page

Question 1.
Find the equation of a straight line which passes through two points (2,2) and (4, -8) which are (x₁, y₁) and (x₂, y₂) respectively.
Note : For drawing a straight line, at least two points are required. Many straight lines can pass through a single point.
Solution:
Here x₁ = 2 y_1- = 2 and x₂ = 4 y₂ = – 8
Formula for constructing a straight line.

Slope (m) = – 5
y intercept = 12
Constant = C
This is of this from y = mx + C
y = 12 – 5x
When x = 0
y = 12
When y = 0
x = \(\frac { 12 }{ 5 }\) = 2.4

Question 2.
Find the solution of the equation system
Solution:
7x₁ – x₂ – x₃ = 0
10x₁ – 2x₂ + x₃ = 8
6x₁ + 3x₂ – 2x₃ = 7

= 7 (4 – 3) + 1 (-20 -6) -1 (30 + 12)
= 7 (1) + 1 (-26) -1 (42)
+ 7 -26 – 42
∆ = – 61

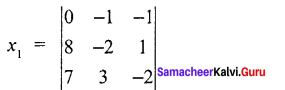
= 0 (4 -3) + 1 (-16 -7) – 1 (24+14)
= 0 + 1 (-23) – 1 (38)
= -23 – 38
= -61

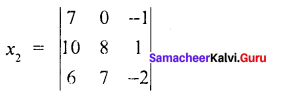
= 7 (-16 – 7) – 0 (- 20 – 6) – 1 (70 – 48)
= 7 ( -23) + 0 (-20 – 6) – 1(70 – 48)
= – 161 – 22
= – 183

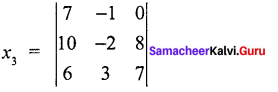
= 7(-14 -24) + 1 (70 – 48) + 1 (30 + 12)
= 7 (-38) + 1 (22) + 0
= – 266 + 22
= – 244

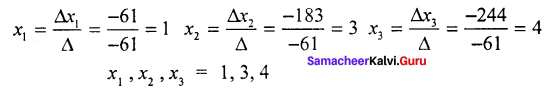
We wish the knowledge shared regarding Samacheer Kalvi for Class 11th Economics Solutions Chapter 12 Mathematical Methods for Economics Questions and Answers has been helpful to you. If you need any further help feel free to ask us and we will get back to you with the possible solution. Bookmark our site to avail the latest updates on different state boards solutions in split seconds.