Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 1.2 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 1.2
கேள்வி 1.
கீழ்க்காணும் தொடர்புகளுக்கு தற்சுட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க.
(i) மிகை முழு எண்களில் தொடர்பு R ஆனது “n-ன் வகுத்தி m ஆக இருந்தால் mR n” என வரையறுக்கப்படுகிறது.
தீர்வு:
மிகை முழு எண்களில் தொடர்பு R ஆனது “‘n-ன் வகுத்தி m ஆக இருந்தால் mRn”.
தற்சுட்டு:
m ஆனது m ஆல் வகுபடும்பொழுது m என்பது அனைத்து மிகை முழுக்கள் ஆகும்.
∴ R என்பது தற்சுட்டுத் தொடர்பு ஆகும்.
சமச்சீர் தொடர்பு:
m R n ⇒ n R m
m ஆனது n -ன் வகுத்தி ⇒ 4-ன் வகுத்தி
2 ≠ 2-ன் வகுத்தி 4
∴ R என்பது சமச்சீர் அல்ல.
கடப்புத் தொடர்பு:
m R n, n R p ⇒ m R p
m ஆனது n -ன் வகுத்தி, n ஆனது p -ன் வகுத்தி
⇒ m ஆனது p -ன் வகுத்தி.
∴ R ஒரு கடப்புத் தொடர்பு எனப்படும்.
∴ R ஒரு தற்சுட்டு, சமச்சீர் மற்றும் கடப்புத் தொடர்பு ஆகும்.
![]()
(ii) P என்பது தளத்திலுள்ள அனைத்து நேர்க்கோடுகளின் கணத்தைக் குறிப்பதாகக் கொள்க. தொடர்பு R என்பது ” ஆனது m-க்குச் செங்குத்தாக இருந்தால் l R m” என வரையறுக்கப்படுகிறது.
தீர்வு:
l, m, n ∈ P என்க.
தற்சுட்டு:
l ஆனது l ற்கு செங்குத்தாக இருக்க முடியாது.
![]()
சமச்சீர் தொடர்பு:
l R m ⇒ m R l
l ஆனது m ற்குச் செங்குத்து
m ஆனது l ற்குச் செங்குத்து.
∴ R என்பது ஒரு சமச்சீர் தொடர்பு.
கடப்புத் தொடர்பு:
l R m மேலும் m R n ≠ l R n
l ஆனது m ற்குச் செங்குத்து
m ஆனது n ற்குச் செங்குத்து
ஆனால் l ஆனது n ற்குச் செங்குத்து ஆக இருக்க முடியாது.
∴ R ஆனது ஒரு கடப்புத் தொடர்பு அல்ல.
⇒ R என்பது சமச்சீர் தொடர்பு மட்டுமே.
(iii) A என்பது ஒரு குடும்பத்தின் உறுப்பினர்கள் அனைவரையும் கொண்ட கணமாகக் கருதுக. “a என்பவர் உன் சகோதரி இல்லையெனில் தொடர்பு ‘Rஆனது aRb” என வரையறுக்கப்படுகிறது.
தீர்வு:
A என்பது ஒரு குடும்பத்தில் உறுப்பினர்கள் அனைவரையும் கொண்ட கணம்.
தொடர்பு R என்பது “a என்பவர் b -ன் சகோதரி இல்லை. a, b, c ∈ A
தற்சுட்டு:
aRa ⇒ a -ஆனது-a-ன் சகோதரி ஆக இருக்க முடியாது.
∴ R ஒரு தற்சுட்டு தொடர்பு.
சமச்சீர் தொடர்பு:
aRb ⇒ bRa
a ஆனது b -ன் சகோதரி அல்ல. b ஆனது a -ன் சகோதரி
∴ R ஒரு சமச்சீர் தொடர்பு அல்ல.
கடப்புத் தொடர்பு:
aRb மற்றும் bRc ⇒ aRc
a ஆனது b -ன் சகோதரி அல்ல.
b ஆனது C-ன் சகோதரி அல்ல.
⇒ a ஆனது C -ன் சகோதரி.
∴ R ஒரு கடப்புத் தொடர்பு அல்ல.
![]()
(iv) A என்பது ஒரு குடும்பத்தின் பெண் உறுப்பினர்கள் அனைவரையும் கொண்ட கணம் என்க. தொடர்பு R என்பது “a என்பவர் -ன் சகோதரி இல்லையெனில் தொடர்பு R ஆனது aRb” என வரையறுக்கப்படுகிறது.
தீர்வு:
a, b, c ∈ A என்க
தற்கட்டு:
a R a ⇒ a ஆனது a -ன் சகோதரி அல்ல.
∴ R ஒரு தற்சுட்டு
சமச்சீர் தொடர்பு:
aRb ⇒ bRa
a-ன் சகோதரி அல்ல.
b -ன் சகோதரி அல்ல.
∴ R ஒரு சமச்சீர் தொடர்பு
கடப்புத் தொடர்பு:
aRb , bRc = aRc
a ஆனவர் b -ன் சகோதரி அல்ல.
b ஆனவர் C -ன் சகோதரி அல்ல.
a ஆனவர் C -ன் சகோதரி ஆவார்.
(எடு) தாய் மகளின் சகோதரி அல்ல, மகள் சித்தியின் சகோதரி அல்ல, ஆனால் தாய் சித்தியின் சகோதரி.
∴ R ஒரு தற்சுட்டு, சமச்சீர், கடப்புத் தொடர்பு ஆகும்.
(v) அனைத்து இயல் எண்களின் கணத்தில் தொடர்பு R என்பது “x + 2y = 1” எனில் xRy என வரையறுக்கப்படுகிறது.
தீர்வு:
x, y ∈ N என்க.
தற்சுட்டு:
x R x ⇒ x + 2x = 1 ⇒ 3x = 1 ⇒ x = \(\frac{1}{3}\) ∉ N
∴ R என்பது தற்சுட்டு தொடர்பு அல்ல.
சமச்சீர் தொடர்பு:
x R x ⇒ y R x, x, y ∈ N
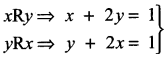
இது x,y-ன் வெவ்வேறு மதிப்புகளுக்கு பொருந்தாது.
∴ R ஒரு சமச்சீர் தொடர்பு அல்ல.
கடப்புத் தொடர்பு:
xRy, yRz ⇒ xRE
xRy, yRz, x, y, z ∈ N மதிப்புகளுக்கு பொருந்தாது.
∴ R ஒரு கடப்புத் தொடர்பு அல்ல.
⇒ R என்பது தற்சுட்டுத் தொடர்பும் அல்ல.
சமச்சீர் தொடர்பும் அல்ல.
கடப்புத் தொடர்பும் அல்ல.
![]()
கேள்வி 2.
X = {a,b,c,d} மற்றும் R = {(a,a), (b, b), (a,c)} என்க. தொடர்பு R-ஐ
(i) தற்சுட்டு
(ii) சமச்சீர்
(iii) கடப்பு
(iv) சமானத் தொடர்பு என உருவாக்க R-உடன் சேர்க்கப்பட வேண்டிய குறைந்தபட்ச உறுப்புகளை எழுதுக.
தீர்வு:
X = {a, b, c, d}
R = {(a, a), (b, b), (a, c)}
(i) R ஒரு தற்சுட்டு ஆக இருக்க (c, c), (d, d) R – ல் சேர்க்கப்பட வேண்டும்.
(ii) R ஒரு சமச்சீர் தொடர்பு ஆக இருக்க R-ல் (c, a) இருக்க வேண்டும்.
(iii) R ஒரு கடப்புத் தொடர்பு ஆக இருக்க R-ல் (c, d), (a, d) இருக்க வேண்டும்.
∴ (a, c), (c, d) ∈ R = (a, d) ∈ R
(iv) R ஒரு தற்சுட்டு, சமச்சீர், கடப்புத் தொடர்பு ஆக இருக்குமேயானால் அது ஒரு சமானத் தொடர்பு ஆகும்.
R-ல் இருக்க வேண்டிய குறைந்த பட்ச உறுப்புகள் {(c,c); (d, d), (c, a)}.
கேள்வி 3.
A = {a,b,c} மற்றும் R = {(a,a), (b, b), (a,c)} என்க. தொடர்பு R-ஐ
(i) தற்சுட்டு
(ii) சமச்சீர்
(iii) கடப்பு
(iv) சமானத் தொடர்பு என உருவாக்க R-உடன் சேர்க்க வேண்டிய குறைந்தபட்ச உறுப்புகளை எழுதுக.
தீர்வு:
(i) ⇒ R = {(a, a), (b, b), (c, c)} ஒரு தற்சுட்டு ஆக இருக்க முடியும்.
(c, c) என்ற உறுப்பு R-ல் சேர்க்கப்பட வேண்டும்.
(ii) R = {(a, a), (b, b), (a, c)} உடன் (c,a) சேர்த்தால் அது ஒரு சமச்சீர் தொடர்பு உடையதாகும்.
(iii) R = {(a, a), (b, a), (a, c)} ஒரு கடப்புத் தொடர்பு ஆகும்.
(iv) R ஒரு சமானத் தொடர்பு ஆக இருக்க அது ஒரு தற்சுட்டு, சமச்சீர், கடப்பு தொடர்பு ஆக இருக்க வேண்டும்.
எனவே குறைந்த பட்ச உறுப்புகள் (c, c) மற்றும் (c, a).
![]()
கேள்வி 4.
ஒரு தளத்திலுள்ள அனைத்து முக்கோணங்களின் கணத்தை P என்போம். P-ல் R என்ற தொடர்பானது “a ஆனது மீன் வடிவொத்ததாக இருப்பின் aRb” என வரையறுக்கப்படுகிறது. R என்பது சமானத் தொடர்பு என நிறுவுக.
தீர்வு:
P ஒரு தளத்திலுள்ள அனைத்து முக்கோணங்களின் கணம் என்க.
P -ல் R என்ற தொடர்பானது ” ஆனது -ன் வடிவொத்தவையாக இருப்பின் aRb” என வரையறுக்கப்படுகிறது.
a, b, c ∈ P என்க.
தற்சுட்டு:
aRa ⇒ a ஆனது a க்கு வடிவொத்தது. a ∈ P
∴ R ஒரு தற்சுட்டு.
சமச்சீர் தொடர்பு:
aRb ⇒ bRa
a ஆனது b க்கு வடிவொத்தது. b ஆனது a க்கு வடிவொத்தது. a, b ∈ P ∴ R ஒரு சமச்சீர் தொடர்பு.
கடப்புத் தொடர்பு:
aRb , bRC ⇒ aRc
a ஆனது b க்கு வடிவொத்தது.
b ஆனது C க்கு வடிவொத்தது.
∴ a ஆனது C க்கு வடிவொத்தது.
a, b, c ∈ P ∴ R ஒரு கடப்புத் தொடர்பு
∴ R ஒரு சமானத் தொடர்பு ஆகும்.
கேள்வி 5.
இயல் எண்களில் கணத்தில் R என்பது “2a + 3b = 30 எனில் aRb” என வரையறுக்கப்படுகிறது. R-ல் உள்ள உறுப்புகளை எழுதுக. அது
(i) தற்சுட்டு
(ii) சமச்சீர்
(iii) கடப்பு
(iv) சமானத் தொடர்பா என்பதை சரிபார்க்க.
தீர்வு:
இயல் எண்க ளின் கணத்தில் R என்பது “2a + 3b = 30 எனில் aRb” என வரையறுக்கப்படுகிறது.
a, b ∈ N ⇒ 2a + 3b= 30
2a + 3b = 30
2a = 30 – 3b
a = \(\frac{30-3 b}{2}\)
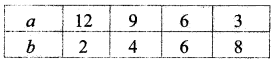
வரிசைச் சோடிகள்: (12, 2), (9, 4), (6, 6), (3, 8)
தற்சுட்டு:
(12, 12) ∉ R ⇒ R ஒரு தற்சுட்டு அல்ல.
சமச்சீர் தொடர்பு:
(9, 4) ∈ R ⇒ (4, 9) ∉ R
∴ R ஒரு சமச்சீர் தொடர்பு அல்ல.
கடப்புத் தொடர்பு: R ஒரு கடப்புத் தொடர்பு ஆக இருக்க முடியாது.
∴ R ஒரு சமானத் தொடர்பாக இருக்க முடியாது.
![]()
கேள்வி 6.
சென்னையில் உள்ள மக்களின் கணத்தில் “நட்பு” ஒரு சமானத் தொடர்பன்று என்பதை நிரூபிக்க.
தீர்வு:
a, b, c ∈ P, P சென்னையில் உள்ள மக்களின் கணம்.
தற்சுட்டு:
a -ஆனது a க்கு நட்பு எனக்கூற இயலாது.
![]()
சமச்சீர் தொடர்பு:
a ஆனது b க்கு நட்பு ⇒ a R b
b ஆனது a க்கு நட்பு ⇒ b R a
∴ R ஒரு சமச்சீர் தொடர்பு கடப்புத்
தொடர்பு:
a ஆனது b க்கு நட்பு ⇒ a R b
b ஆனது C க்கு நட்பு ⇒ b R c
a ஆனது C க்கு நட்பு ஆக இருக்க வேண்டியது இல்லை.
∴ R ஒரு கடப்புத் தொடர்பு அல்ல.
∴ Rஒரு சமானத் தொடர்பன்று என நிரூபிக்கப்பட்டது.
கேள்வி 7.
இயல் எண்களில் கணத்தில் தொடர்பு R ஆனது
“a + b ≤ 6 ஆக இருந்தால் aRb” என வரையறுக்கப் படுகிறது. R-ல் உள்ள உறுப்புகளை எழுதுக. அது
(i) தற்சுட்டு
(ii) சமச்சீர்
(iii) கடப்பு
(iv) சமானத் தொடர்பு என்பதை சரிபார்க்க.
தீர்வு:
a + b ≤ 6,a,b ∈ N; a R b எனத் தொடர்புபடுத்தப்படுகிறது.
a + b ≤ 6 ⇒ a ≤ 6 – b
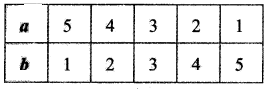
வரிசைச் சோடிகள் (5, 1), (4,12), (3, 3), (2, 4), (1, 5)
தற்சுட்டு : (5, 5) ∉ R
∴ R ஒரு தற்சுட்டு அல்ல.
சமச்சீர் தொடர்பு:
(5,1) ∈ R (1,5) ∈ R
(2,4) ∈ R (4,2) ∈ R
∴ R ஒரு சமச்சீர்.
கடப்புத் தொடர்பு:
(4, 2) ∈ R
(2,4) ∈ R ⇒ (4,4) ∉ R
∴ R ஒரு கடப்புத் தொடர்பு அல்ல;
∴ R ஒரு சமானத் தொடர்பு அல்ல.
![]()
கேள்வி 8.
A = {a,b,c} என்க. A-ன் மீதான மிகச்சிறிய செவ்வெண்மையுடைய சமானத் தொடர்பு என்ன? A-ன் மீதான மிகப் பெரிய செவ்வெண்மையுடைய சமானத் தொடர்பு என்ன?
தீர்வு:
A = {a, b, c} என்க .
(i) R = {(a, a), (b, b), (c,c)}
R ஒரு தற்சுட்டு, சமச்சீர் மற்றும் கடப்புத் தொடர்பு
R ஒரு சமானத் தொடர்பு ஆகும்.
n(R) = Aன் மீதான மிகச்சிறிய செவ்வெண்மை உடைய சமானத் தொடர்பு n(R) = 3
(ii) R = {(a, a), (a , b), (a, c), (b, b), (b, a), (b, c), (c, a), (c, b), (c, c) } என்க
R ஒரு தற்சுட்டு ∵ (a, a), (b, b), (c, c) ∈ R
R ஒரு சமச்சீர் தொடர்பு
∵ (a, b) ∈ R ⇒ (b, a) ∈ R
(b, c) ∈ R ⇒ (c, b) ∈ R
(c, a) ∈ R ⇒ (a, c) ∈ R
R ஒரு கடப்புத் தொடர்பு
∵ (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R
∵ R என்பது A-ன்
மீதான மிகப்பெரிய செவ்வெண்மையுடைய சமானத் தொடர்பு ஆகும்.
n(R) = 9.
![]()
கேள்வி 9.
Zல் “m- n ஆனது 7 ஆல் வசப்படுமெனில் mRn” எனத் தொடர்பு R வரையறுக்கப்பட்டால் R என்பது சமானத் தொடர்பு என நிரூபிக்க.
தீர்வு:
m – m = 0
m – m ஆனது 7 ஆல் வகுபடும் ⇒ m Rm
∴ R ஒரு தற்சுட்டு.
m R n எனில் m – n = 7k, K ∈ Z
n – m = 7 ( – K), – K ∈ Z
∴ R ஒரு சமச்சீர் தொடர்பு.
mRn, nRp
⇒ m – n = 7k ⇒ m = 7K + n
n – p = 7l ⇒ – p = 7l – n
![]()
m = p + 7(K + l) ⇒ m R p
∴ R ஒரு கடப்புத் தொடர்பு;
∴ R ஒரு சமானத் தொடர்பு