Samacheer Kalvi 11th Maths Guide Chapter 1 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 1.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 1.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 1.4

கேள்வி 1.
கொடுக்கப்பட்டுள்ள படத்தில் y = x³ என்ற வளை வரையின் படத்தினைப் பயன்படுத்தி அச்சு மதிப்பு மாறாமல் ஒரே தளத்தில் கீழ்க்காணும் சார்புகளை வரைக.
(i) y = -x³
(ii) y = x³ + 1
(iii) y = x³ – 1
(iv) y = (x + 1)³

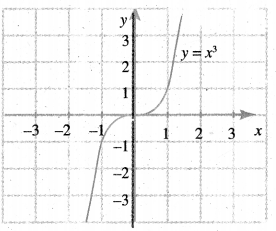
தீர்வு:
(i) y = -x³

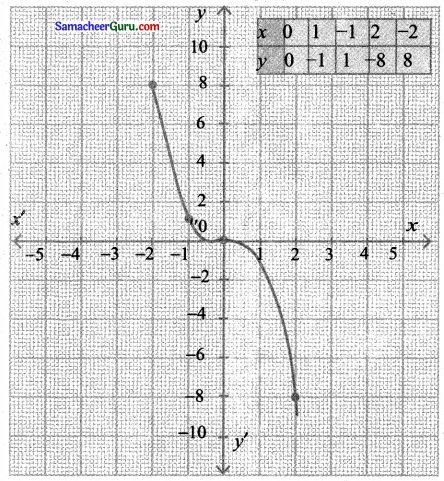
y = f(x) = x³
y = – f(x) = – x³
இது y = f(x) -ன் x ஐப் பொறுத்து நேர்மாறு வரைபடம் ஆகும்.

(ii) y = x³ + 1

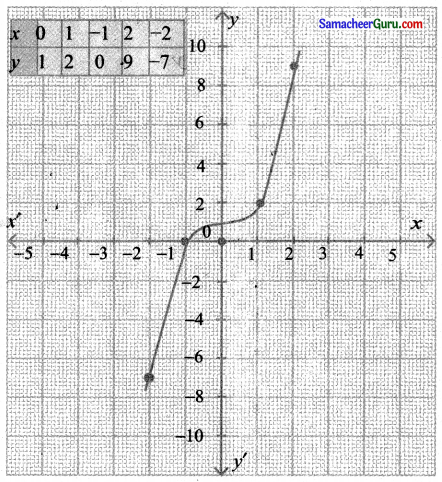
f(x) = x³
y = f(x) + 1
இது f(x)-ன் வரைபடத்தில் ஓரலகு மேல்நோக்கி நகர்வால் கிடைப்பது ஆகும்.

(iii) y = x³ – 1

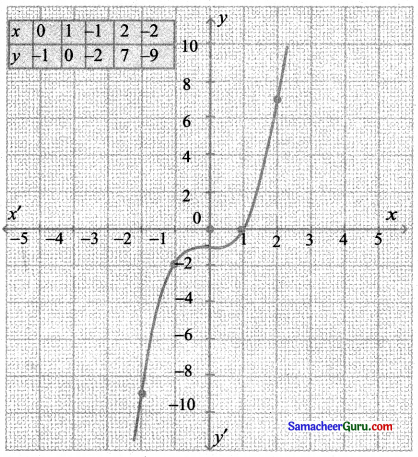
f(x) = x³
y = f(x) – 1
இந்த வரைபடம் f(x) -ன் வரைபடத்தில் ஓரலகு கீழ்நோக்கி நகர்வால் கிடைப்பது ஆகும்.

(iv) y = (x + 1)³

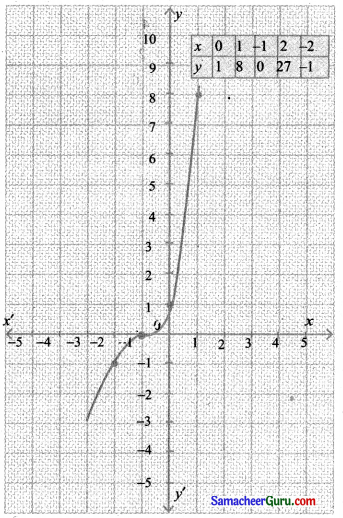
f(x) = x³
y = (x + 1)³ இதன் வரைபடம் f(x) வரைபடத்தை ஓரலகு இடப்பக்க நகர்வால் கிடைக்கப் பெறுவது ஆகும்.

கேள்வி 2.
கொடுக்கப்பட்டுள்ள படத்தில் y = \(x^{\left(\frac{1}{3}\right)}\) என்ற வளை
வரையைப் பயன்படுத்திக் கீழ்க்காணும் சார்புகளை ! ஒரே தளத்தில் வரைக.
(i) y = –\(x^{\left(\frac{1}{3}\right)}\)
(ii) y = \(x^{\left(\frac{1}{3}\right)}\) + 1
(iii) y = \(x^{\left(\frac{1}{3}\right)}\) – 1
(iv) y = \((x+1)^{\left(\frac{1}{3}\right)}\)
தீர்வு:
(i) y = –\(x^{\left(\frac{1}{3}\right)}\)

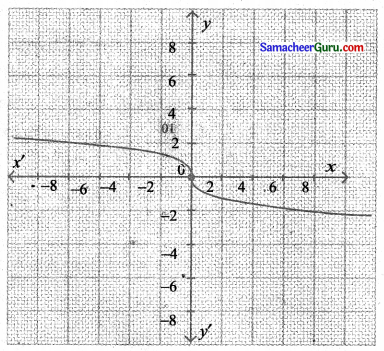
y = –\(x^{\left(\frac{1}{3}\right)}\) என்பது x அச்சினைப் பொறுத்து y = \(x^{\left(\frac{1}{3}\right)}\) -ன் பிரதிபலிப்பு ஆகும்.

(ii) y = \(x^{\left(\frac{1}{3}\right)}\) + 1

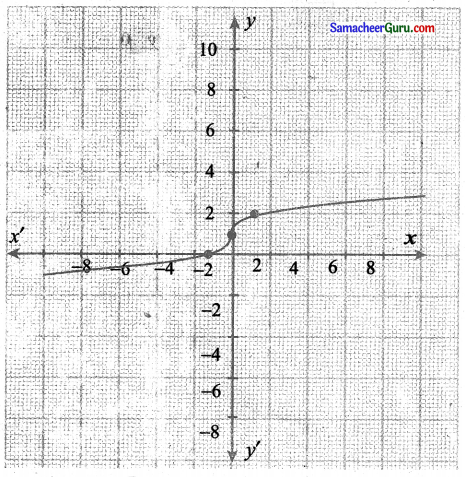
y = \(x^{\left(\frac{1}{3}\right)}\)
y = \(x^{\left(\frac{1}{3}\right)}\) + 1 என்பது y = \(x^{\left(\frac{1}{3}\right)}\) + 1 வரைபடத்தை நோக்கி நகர்வால் கிடைக்கப்பெறுவது ஆகும்.

(iii) y = \(x^{\left(\frac{1}{3}\right)}\) – 1

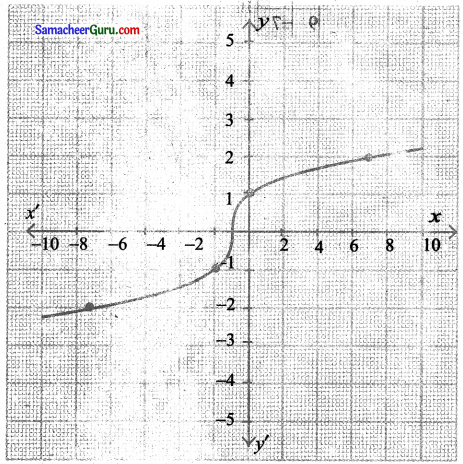
y = \(x^{\left(\frac{1}{3}\right)}\)
ன் y = \(x^{\left(\frac{1}{3}\right)}\) – 1 ன் வரைபடம் \(x^{\left(\frac{1}{3}\right)}\) வரைபடத்தை ஓரலகு மேல் கீழ்நோக்கி நகர்வால் கிடைக்கப் பெறுவதாகும்.

(iv) y = \((x+1)^{\left(\frac{1}{3}\right)}\)

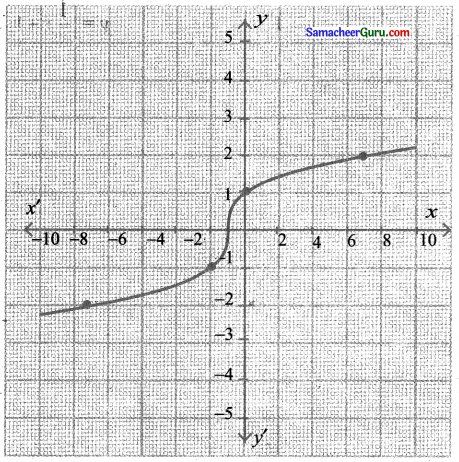
இதன் வரைபடம் y = \(x^{\left(\frac{1}{3}\right)}\) வரைபடத்தை ஓரலகு தூரம் கிடைமட்டமாக இடப்பக்கம் நோக்கி நகர்த்துகிறது.

கேள்வி 3.
ஒரே தளத்தில் f(x) = x³ மற்றும் g(x) = \(\sqrt[3]{x}\) சார்புகளை வரைபடமாக்குக. fog -ஐ கணித்து அதே தளத்தில் வரைபடமாக்குக. முடிவுகளை ஆய்வு செய்க.
தீர்வு:
கொடுக்கப்பட்டது: f(x) = x³ g(x) = \(x^{\left(\frac{1}{3}\right)}\)


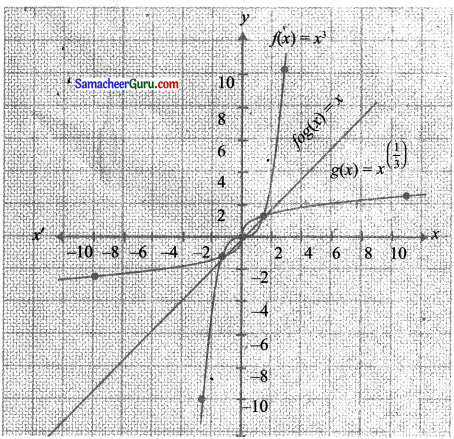
fog (x) = x ஆனது y = x நேர்க்கோட்டைப் பொறுத்து சமச்சீராக இருக்கும். g(x) ஆனது f(x)-ன் நேர் மாறாகும்.
∴ g(x) = f¹ (x)

கேள்வி 4.
y = x² என்ற வளைவரையிலிருந்து y = 3 (x – 1)² + 5 என்ற வளைவரையை காணும் படிநிலைகளை எழுதுக.
தீர்வு:
படி 1:
y = x² யின் வரைபடம் வரைக.

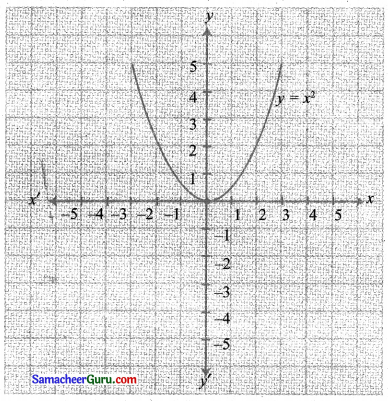
படி 2: y = (x – 1)² ஓரலகு வலது புறத்தில் நகர்த்த ப்பட்டு
வரையப்படுகிறது.

படி 3: y = 3(x – 1)² – ன் வரைபடம் y -அச்சை நோக்கி
அழுத்தப்பட்டு அதாவது x அச்சிலிருந்து விலகுவதால் வரையப்படுகிறது. ஏனென்றால் (x – 1)² ஆனது 3 ஆல் பெருக்கப்பட்டு பெறப்படுகிறது. 3 > 1

படி 4 : y = 3(x – 1)² + 5-ன் வரைபடம் 5 அலகுகள் மேல்நோக்கி நகர்வதால் பெறப்படுகிறது.

கேள்வி 5.
y = sin x என்ற சார்பினை வரைந்து அதன் மூலம்
(i) y = sin (-x)
(ii) y = -sin (-x)
(i) y = sin\(\left(\frac{\pi}{2}+x\right)\)
(iv) y = sin\(\left(\frac{\pi}{2}-x\right)\)
ஆகியவற்றை வரைக. (இங்கு (iii), (iv), என்பவை cos X
என்பது முக்கோணவியல் மூலம் தெரிந்து கொள்ளலாம்).
தீர்வு:
(i) y = sin (-x)

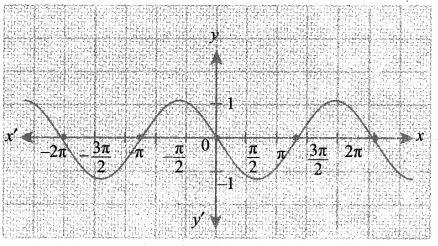
y = -sin x-ன் வரைபடம் y = sin x- வரைபடத்தின் y – அச்சை பொறுத்த பிரதிபலிப்பு வரைபடமாகும்.

(ii) y = -sin (-x)

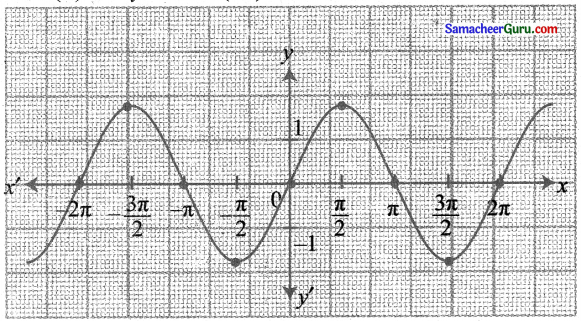
y = – sin (-x)-ன் வரைபடம் x அச்சைப் பொறுத்து sin (-x) ன் பிரதிபலிப்பு வரைபடமாகும்.

(iii) y = sin\(\left(\frac{\pi}{2}+x\right)\)
y = sin x
sin \(\left(\frac{\pi}{2}+x\right)\) -ன் வரைபடம் sin x வரைபடத்தை \(\frac{\pi}{2}\) அலகுகள் இடப்பக்க நகர்வினால் பெறப்படுகிறது.

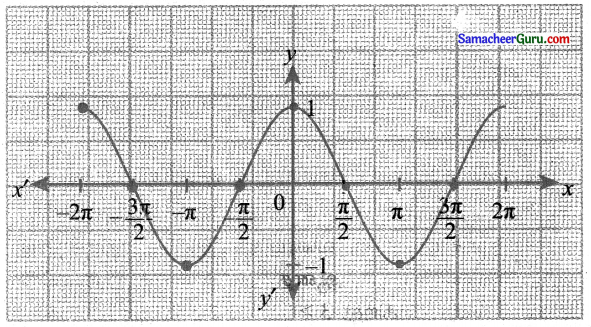
(iv) y = sin\(\left(\frac{\pi}{2}-x\right)\)

y = sin x
sin\(\left(\frac{\pi}{2}-x\right)\) -ன் வரைபடம் sin (-x)-ன் வரைபடத்தை \(\frac{\pi}{2}\) அலகுகள் வலப்பக்க நகர்வினால் பெறப்படுகிறது.

கேள்வி 6.
y = x என்ற நேர்கோட்டின் மூலம்
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y = \(\frac{1}{2}\)x + 1
(v) 2x + y + 3 = 0 ஆகியவற்றைத் தோராயமாக வரைக.
தீர்வு:
(i) y = -x

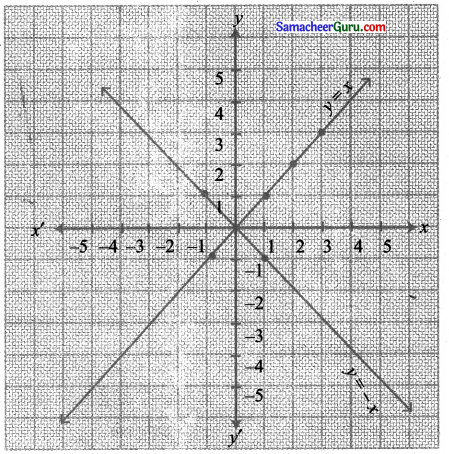
y = – x-ன் வரைபடம்
y = x வரைபடத்தின் x அச்சை ஒத்த பிரதிபலிப்பு ஆகும்.

(ii) y = 2x

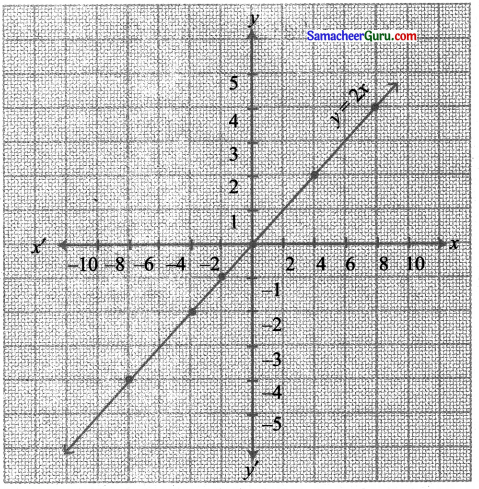
y = 2x என்பது y அச்சை நோக்கி அழுத்தப்படுவதால் வரையப்படுகிறது. ஏனென்றால் இங்கு பெருக்கும் காரணி 2
∵ 2 > 1

(iii) y = x + 1

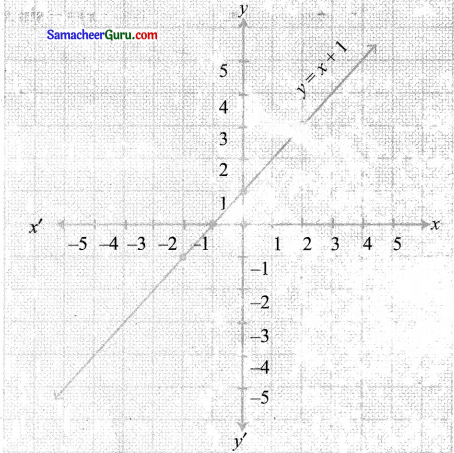
y = x + 1 வரைபடம் ஓர் அலகு மேல்நோக்கி நகர்வதால் பெறப்படுகிறது.

(iv) y = \(\frac{1}{2}\)x + 1

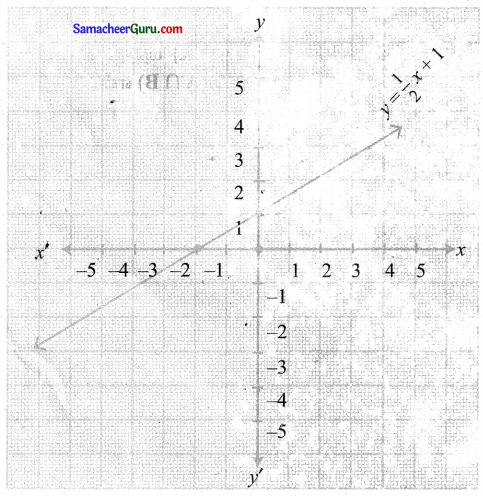
வரைபடம் x அச்சை நோக்கி பெறப்படுகிறது ஏனென்றால் பெருக்கப்படும் காரணி \(\frac{1}{2}\) < 1 மேலும் ஓரலகு மேல் நோக்கி நகர்வதால் பெறப்படுகிறது.

(v) 2x + y + 3 = 0 ⇒ y = – 2x – 3

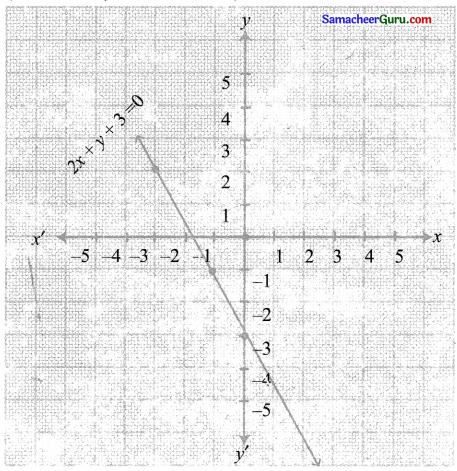
வரைபடம் – 2 < 1
∴ x அச்சை நோக்கி 3 அலகுகள் கீழ்நோக்கி நகர்வதால் பெறப்படுகிறது.

கேள்வி 7.
y = |x| என்ற வளைவரையின் மூலம்
(i) y = |x – 1| + 1
(ii) y = |x + 1| – 1
(iii) y = |x + 2| + 3 ஆகியவற்றை வரைக.
தீர்வு:
(i) y = |x – 1| + 1

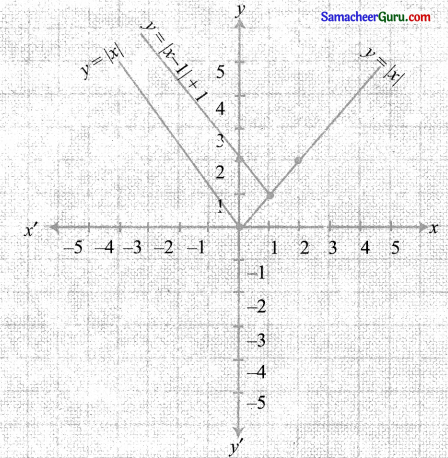
வரைபடம் ஓரலகு வலப்புறமாக மேல்நோக்கி நகர்வதால் பெறப்படுகிறது.

(ii) y = |x + 1| – 1

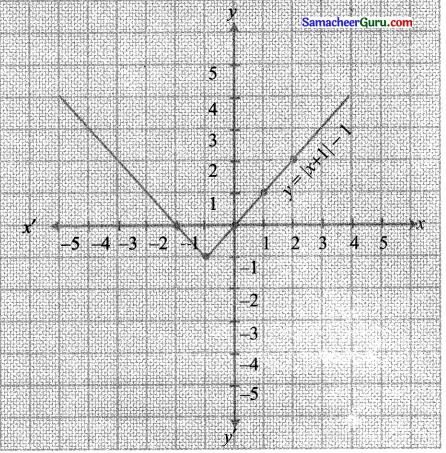
வரைபடம் ஓரலகு இடப்புறமாக கீழ்நோக்கி நகர்வதால் பெறப்படுகிறது.

(iii) y = |x + 2| + 3

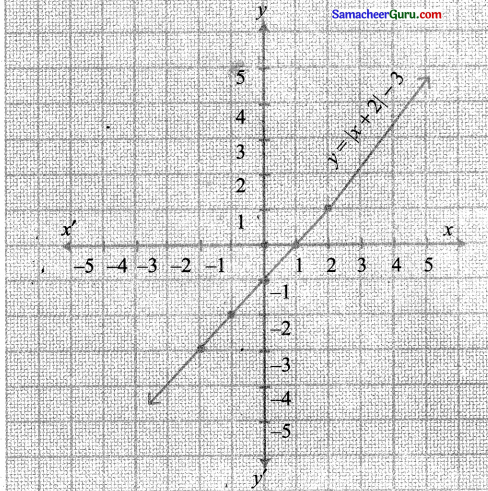
வரைபடம் 2 அலகுகள் இடது புறமாக மற்றும் 3 அலகுகள் கீழ்ப்புறமாக நகர்த்துவதால் பெறப்படுகிறது.

கேள்வி 8.
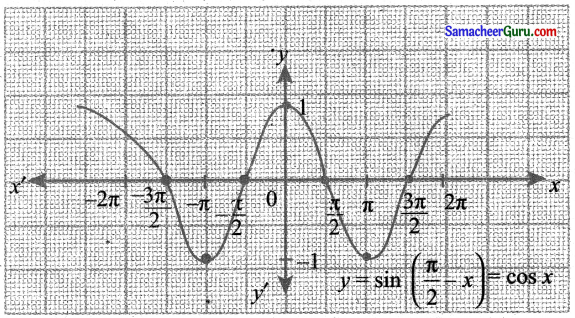
y = sin x என்ற வளைவரை மூலம் y = sin|x| என்பதன் வரைபடத்தை வரைக. [இங்கு sin(-x)= – sin x].
தீர்வு:
y = sin |x|


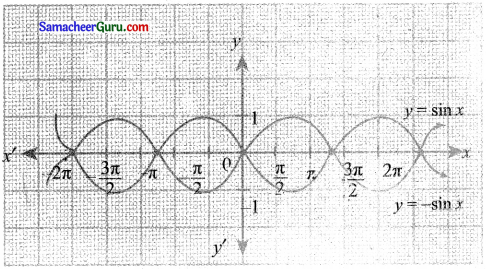
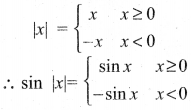
y = sin (-x) என்ற வரைபடமானது –sinx வரைபடத்தின் பிரதிபலிப்பாகும்.