Samacheer Kalvi 11th Maths Guide Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 10 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 10.4 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.4

கீழ்க்காண்பவற்றை வகையிடுக (1 – 18) :

Question 1.
y = x^{cos x}
தீர்வு :
log y = log x^{cos x}
⇒ log y = cos x. logx
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = cos x . \(\frac{d}{d x}\) (log x) + log x . \(\frac{d}{d x}\)(cos x)

\(\frac{1}{y} \cdot \frac{d y}{d x}\) = cos x × \(\frac{1}{x}\) + log x(-sin x)

= \(\frac{\cos x}{x}\) – sin x . log x

⇒ \(\frac{d y}{d x}\) = y[\(\frac{\cos x}{x}\) – sin x . log x]
⇒ \(\frac{d y}{d x}\) = x^{cos x}[\(\frac{\cos x}{x}\) – sin x . log x]

Question 2.
y = x^{log x} + (log x)^x
தீர்வு :
y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\) ………..(1)
u = x^{log x} என்க .
இரு புறமும் மடக்கை எடுக்க
log u = log x^{log x} = log x. log x = (log x)²
\(\frac{1}{u} \frac{d u}{d x}\) = 2 log x × \(\frac{1}{x}\)
= \(\frac{2 \log x}{x}\)

⇒ \(\frac{d u}{d x}\) = u(\(\frac{2 \log x}{x}\))
= x^{log x} \(\frac{2 \log x}{x}\) …………..(2)
மற்றும் v = (log x)^x
இருபுறமும் மடக்கை எடுக்க
log v = log ((log x}^x) = x. log (log x)

\(\frac{1}{v} \frac{d v}{d x}\) = x . \(\frac{d}{d x}\) (log(log x)) + log(log x) × \(\frac{d}{d x}\)(1)

= x . \(\frac{1}{log x}\) × \(\frac{1}{x}\) + log(log x)
= \(\frac{1}{log x}\) + log(log x)

⇒ \(\frac{d v}{d x}\) = v[\(\frac{1}{log x}\) + log(log x)] + (log x)^x(\(\frac{1}{log x}\) + log(log x)) ……………(3)
(2), (3) ஐ (1) ல் பிரதியிட
\(\frac{d y}{d x}\) = x^{log x}(\(\frac{2 \log x}{x}\)) + (log x)^x [\(\frac{1}{log x}\) + log(log x)]

Question 3.
\(\sqrt{x y}\) = e^{(x – y)}
தீர்வு :
\(\sqrt{x y}\) = e^{(x – y)}
⇒ (xy)^{\(\frac{1}{2}\)} = e^{(x – y)}
இருபுறமும் மடக்கை எடுக்க.
\(\frac{1}{2}\) log xy = (x – y) log_e e
⇒ \(\frac{1}{2}\) [log x + log y] = x – y [∵ log_e e = 1]

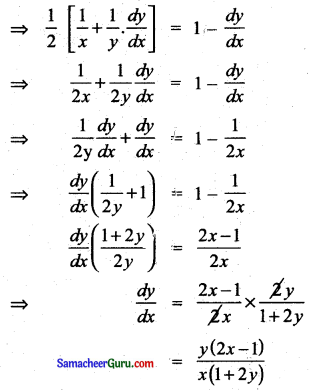
Question 4.
x^y = y^x
தீர்வு :
இருபுறமும் மடக்கை எடுக்க,
y log x = x log y
⇒ y × \(\frac{1}{x}\) × \(\frac{d y}{d x}\) = x × \(\frac{1}{y}\) \(\frac{d y}{d x}\) + log y(1)

⇒ \(\frac{y}{x}\) + log x(\(\frac{d y}{d x}\)) = \(\frac{x}{y}\) \(\frac{d y}{d x}\) + log y

⇒ \(\frac{d y}{d x}\) (log x – \(\frac{x}{y}\)) = log y – \(\frac{y}{x}\)

⇒ \(\frac{d y}{d x}\) (\(\frac{y \log x-x}{y}\)) = \(\frac{x \log y-y}{x}\)

⇒ \(\frac{d y}{d x}\) = \(\frac{y(x \log y-y)}{x(y \log x-x)}\)

Question 5.
(cos x)^logx
தீர்வு :
y = (cos x)^{log x}
இருபுறமும் மடக்கை எடுக்க
log y = log x. log (cos x)
\(\frac{1}{y}\) \(\frac{d y}{d x}\) = log x . \(\frac{d}{d x}\) log(cos x) + log(cos x) \(\frac{d}{d x}\) (log x)

⇒ \(\frac{1}{y}\) \(\frac{d y}{d x}\) = log x × \(\frac{1}{\cos x}\) (-sin x) + log(cos x) × \(\frac{1}{x}\)

⇒ \(\frac{1}{y}\) \(\frac{d y}{d x}\) = -log x tan x + \(\frac{\log (\cos x)}{x}\)

⇒ \(\frac{d y}{d x}\) = y[\(\frac{\log (\cos x)}{x}\) – log x . tan x]

⇒ \(\frac{d y}{d x}\) = (cos x)^{log x} [\(\frac{\log (\cos x)}{x}\) – log x . tan x]

Question 6.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
தீர்வு :

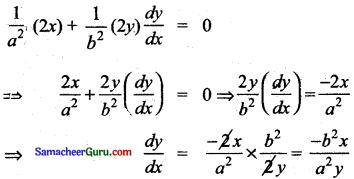
Question 7.
\(\sqrt{x^{2}+y^{2}}\)) = tan^-1 (\(\frac{y}{x}\))
தீர்வு :
\(\sqrt{x^{2}+y^{2}}\)) = tan^-1 (\(\frac{y}{x}\))

Question 8.
tan(x + y) + tan(x – y) = x
தீர்வு :
sec² (x + y) \(\frac{d}{d x}\) (x + y) + sec² (x – y) . \(\frac{d}{d x}\) (x – y) = 1

⇒ sec² (x + y) [1 + \(\frac{d y}{d x}\)] + sec² (x – y) [1 – \(\frac{d y}{d x}\)] = 1

⇒ sec²(x + y) + sec² (x + y) . \(\frac{d y}{d x}\) + sec² (x – y) – sec² (x – y) \(\frac{d y}{d x}\) = 1

⇒ \(\frac{d y}{d x}\) [sec² (x + y) – sec² (x – y)] = 1 – sec² (x + y) – sec² (x – y)

⇒ \(\frac{d y}{d x}\) = \(\frac{1-\sec ^{2}(x+y)-\sec ^{2}(x-y)}{\sec ^{2}(x+y)-\sec ^{2}(x-y)}\)

Question 9.
cos (xy) = x எனில் \(\frac{d y}{d x}\) = \(\frac{-(1+y \sin (x y))}{x \sin x y}\) எனக்காட்டுக. x தீர்வு :
cos (xy) =x
‘x’ ஐப் பொறுத்து உட்படு வகையிடல் காண
– sin (xy). \(\frac{d}{d x}\)(xy) = 1

⇒ -sin(xy) . \(\frac{d}{d x}\) (xy) = 1

⇒ x sin (xy) \(\frac{d y}{d x}\) – y sin (xy) = 1

⇒ x sin (xy) \(\frac{d y}{d x}\) = 1 + y sin (xy)

⇒ \(\frac{d y}{d x}\) = \(\frac{-(1+y \sin (x y))}{\dot{x} \sin (x y)}\)
எனவே நிருபிக்கப்பட்டது.

Question 10.
\(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\)
தீர்வு :
y = \(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\) என்க.
[∵ 2 sin² \(\frac{x}{2}\) = 1 – cos x மற்றும் 2 cos² \(\frac{x}{2}\) = 1 + cos x]

⇒ y = \(\tan ^{-1} \sqrt{\frac{2 \sin ^{2} \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}}\)

= \(\tan ^{-1} \sqrt{\tan ^{2} \frac{x}{2}}=\tan ^{-1}\left(\tan \frac{x}{2}\right)\)

⇒ y = \(\frac{x}{2}\)

∴ \(\frac{d y}{d x}\) = \(\frac{1}{2}\) (1) = \(\frac{1}{2}\)

Question 11.
\(\tan ^{-1}\left(\frac{6 x}{1-9 x^{2}}\right)\)
தீர்வு :
y = \(\tan ^{-1}\left(\frac{6 x}{1-9 x^{2}}\right)\) என்க.

Question 12.
\(\cos \left(2 \tan ^{-1} \sqrt{\frac{1-x}{1+x}}\right)\)
தீர்வு :
y = cos(2 \(\tan ^{-1} \sqrt{\frac{1-x}{1+x}}\)) என்க.
x = cos θ என்க.

⇒ y = cos(2 tan^-1 \(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}\))

⇒ y = cos(2 tan^-1 \(\sqrt{\frac{2 \sin ^{2} \frac{\theta}{2}}{2 \cos ^{2} \frac{\theta}{2}}}\))

⇒ y = cos(2 tan^-1\(\sqrt{\tan ^{2} \frac{\theta}{2}}\))

⇒ y = cos(2 tan^-1 \(\left(\tan \frac{\theta}{2}\right)\))

⇒ y = cos()

⇒ y = cos θ [x = cos θ]

⇒ y = x ⇒ \(\frac{d y}{d x}\) = 1

Question 13.
x = acos³ t; y = a sin³ t
தீர்வு :
\(\frac{d x}{d t}\) = a . 3 cos² t \(\frac{d}{d t}\) (cos t)
= 3a cos² t (-sin t)
= -3a sin t cos² t

y = a sin³ t
\(\frac{d y}{d t}\) = 3a sin² t . \(\frac{d}{d t}\) (sin t)
= 3a sin² t cos t

∴ \(\frac{d y}{d x}\) = \(\frac{d y}{d t}\) × \(\frac{d t}{d x}\)
= \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\)
= \(\frac{3 a \sin ^{2} t \cos t}{-3 a \sin t \cos ^{2} t}\)
= – \(\frac{\sin t}{\cos t}\) = -tan t

Question 14.
x = a(cos t + t sin t); y = a(sin t – t cos t)
தீர்வு :
x = a(cos t + t sin t); y = a(sin t – t cos t)
\(\frac{d x}{d t}\) = a(-sin t + t cos t + sin t) = a . (t cos t)
y = a (sin t – t cos t)
\(\frac{d y}{d t}\) = a(cos t – t(-sin t) – cos t)
= a(cos t + t sin t – cos t) = at sin t
∴ \(\frac{d y}{d x}\) = \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\) = tex]\frac{a t \sin t}{a t \cos t}[/latex] = tan t

Question 15.
x = \(\frac{1-t^{2}}{1+t^{2}}\), y = \(\frac{2 t}{1+t^{2}}\)
தீர்வு :
\(\frac{d x}{d t}\) = \(\frac{\left(1+t^{2}\right)(-2 t)-\left(1-t^{2}\right)(2 t)}{\left(1+t^{2}\right)^{2}}\)

= \(\frac{-2 t-2 t^{3}-2 t+2 t^{3}}{\left(1+t^{2}\right)^{2}}\)

= \(\frac{-4 t}{\left(1+t^{2}\right)^{2}}\)

y = \(\frac{2 t}{1+t^{2}}\)

\(\frac{d y}{d t}\) = \(\frac{\left(1+t^{2}\right)(2)-2 t(2 t)}{\left(1+t^{2}\right)^{2}}\)

= \(\frac{2+2 t^{2}-4 t^{2}}{\left(1+t^{2}\right)^{2}}\)

= \(\frac{2-2 t^{2}}{\left(1+t^{2}\right)^{2}}\)

= \(\frac{2\left(1-t^{2}\right)}{\left(1+t^{2}\right)^{2}}\)

∴ \(\frac{d y}{d x}\) =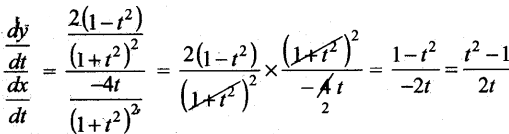

Question 16.
cos^-1 (\(\frac{1-x^{2}}{1+x^{2}}\))
தீர்வு :
y = cos^-1 (\(\frac{1-x^{2}}{1+x^{2}}\))
x = tan θ என்க
⇒ θ = tan^-1 x
∴ y = cos^-1(\(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\))

= cos^-1 (cos 2θ) [∵ cos 2θ = \(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\)]
y = 2θ

⇒ y = 2. tan^-1 x
\(\frac{d y}{d x}\) = 2 × \(\frac{1}{1+x^{2}}\) = \(\frac{2}{1+x^{2}}\)

Question 17.
sin^-1(3x – 4x³)
தீர்வு :
y = sin^-1(3x – 4x³) என்க
x = sin θ
θ = sin^-1 x
∴ y = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1(sin 3θ)
[∵ sin 3θ = 3 sin θ – 4 sin³ θ]
y = 3θ = 3 sin^-1 x
∴ \(\frac{d y}{d x}\) = 3 × \(\frac{1}{\sqrt{1-x^{2}}}\)
= \(\frac{3}{\sqrt{1-x^{2}}}\)

Question 18.
\(\tan ^{-1}\left(\frac{\cos x+\sin x}{\cos x-\sin x}\right)\)
தீர்வு :
y = \(\tan ^{-1}\left(\frac{\cos x+\sin x}{\cos x-\sin x}\right)\) ………..(1)
tan y = \(\frac{\cos x+\sin x}{\cos x-\sin x}\)
தொகுதி, பகுதியை cos x- ஆல் வகுக்க
=
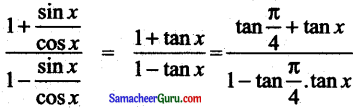
[∵ tan \(\frac{pi}{4}\) = 1] ………….(2)
= tan (\(\frac{pi}{4}\) + x)
(2) ஐ(1) ல் பிரதியிட,
y = tan^-1 (tan(\(\frac{pi}{4}\) + x))
y = \(\frac{pi}{4}\) + x
∴ \(\frac{d y}{d x}\) = 0 + 1 = 1

Question 19.
x² -ஐபொறுத்து sin x² -ன் வகைக்கெழுவைக் காண்க.
தீர்வு :
u = sin x² மற்றும் v = x²
⇒ \(\frac{d u}{d x}\) = cos(x²) . \(\frac{d}{d x}\) (x²) = 2x cos x²

மற்றும் \(\frac{d v}{d x}\) = 2x
\(\frac{d u}{d x}\) = \(\frac{d u}{d x}\) / \(\frac{d v}{d x}\)
= \(\frac{2 x \cdot \cos x^{2}}{2 x}\)

\(\frac{d u}{d v}\) = cos x²

Question 20.
tan^-1 x-ஐ பொறுத்து sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\) கெழுவைக் காண்க.
தீர்வு :
u = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
v = tan^-1 x
u = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
x = tan θ என்க
θ = tan^-1 x
∴ u = sin^-1 (\(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\))
= sin^-1(sin 2θ) = 2θ
= 2 tan^-1 x

∴ \(\frac{d u}{d x}\) = \(\frac{2}{1+x^{2}}\) மற்றும்
\(\frac{d u}{d x}\) = \(\frac{1}{1+x^{2}}\)

∴ \(\frac{d u}{d v}\) = \(\frac{d u}{d x}\) / \(\frac{d v}{d x}\) = \(\frac{\frac{2}{1+x^{2}}}{\frac{1}{1+x^{2}}}\)

∴ \(\frac{d u}{d v}\) = \(\frac{2}{1+x^{2}} \times \frac{1+x^{2}}{1}\) = 2

∴ \(\frac{d u}{d v}\) = 2

Question 21.
u = tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), v = tan^-1 x களில் \(\frac{d u}{d v}\) காண்க.
தீர்வு :
u = tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\) பொறுத்து v = tan^-1 x

x = tan θ என்க

⇒ θ = tan^-1 x

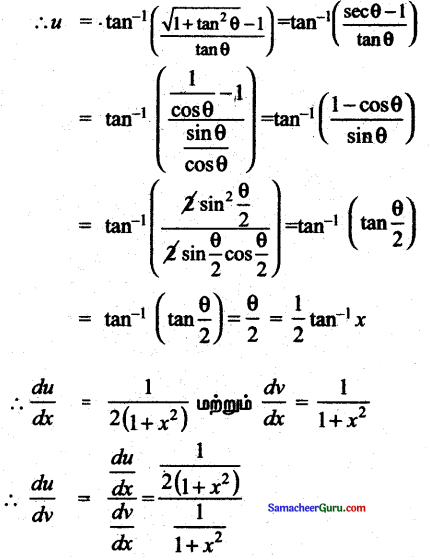
= \(\frac{1}{2\left(1+x^{2}\right)} \times \frac{1+x^{2}}{1}\)

∴ \(\frac{d u}{d v}\) = \(\frac{1}{2}\)

Question 22.
\(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)\) x’-ஐப் பொறுத்து \(\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)\) வகைக்கெழுவைக் காண்க.
தீர்வு :
u = \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)\)

v = \(\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)\) என்க

u = tan^-1 (\(\frac{2 \sin \frac{x}{2} \cos \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}\))

[∵ sin 2θ = 2 sin θ cos θ, 1 + cos 2θ = 2 cos² θ]

u = tan^-1 (tan \(\frac{x}{2}\))
⇒ u = \(\frac{1}{2}\)

∴ \(\frac{d u}{d x}\) = \(\frac{1}{2}\)
மற்றும் v = \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)\)

v = \(\tan ^{-1} \frac{\sin \left(\frac{\pi}{2}+x\right)}{1-\cos \left(\frac{\pi}{2}+x\right)}\)

Question 23.
y = sin^-1 x எனில், y” காண்க.
தீர்வு :
y = sin^-1 x
y’ = \(\frac{1}{\sqrt{1-x^{2}}}\) = (1 – x²)^{\(-\frac{1}{2}\)}

∴ y” = \(-\frac{1}{2}\) (1 – x²)^{\(-\frac{1}{2}\) – 1} \(\frac{d}{d x}\) (1 – x²)

y” = \(-\frac{1}{2}\) (1 – x²)^{\(-\frac{3}{2}\)} (-2x)

= x(1 – x²)^{\(-\frac{3}{2}\)}
y” = \(\frac{x}{\left(1-x^{2}\right)^{\frac{3}{2}}}\)

Question 24.
y = e^tan-1 எனில், (1 + x²) y” + (2x -1)y’ = 0 எனக்காட்டுக.
தீர்வு :
y = e^tan-1
y’ = e^tan-1 . \(\frac{d}{d x}\)(tan^-1 x)
⇒ y’ = e^tan-1\(\frac{1}{1+x^{2}}\)

⇒ (1 + x²) y’ = y [∵ y = e^tan-1]
‘x’-ஐப் பொறுத்து வகைப்படுத்த
(1 + x²)y” + y'(2x) = y’
⇒ (1 + x²)y” + 2xy’ – y’ = 0
⇒ (1 + x²)y” + (2x – 1)y’ = 0
எனவே நிருபிக்கப்பட்டது.

Question 25.
y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\) எனில், (1 – x²)y₂ – 3xy₁ – y = 0 வகைப்படுத்த.
தீர்வு :
y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\)
⇒ y\(\sqrt{1-x^{2}}\) = sin^-1 x
ஆல் இருபுறமும் வகுக்க’
y²(1 – x²) = (sin^-1 x)²
x-ஐப் பொறுத்து மீண்டும் வகைப்படுத்த
y²(-2x) + (1 – x²) 2yy’ = 2 . sin^-1 x . \(\frac{d}{d x}\) (sin^-1 x)
⇒ -2xy² + (1 – x²) 2yy’ = 2 . sin^-1 x . \(\frac{1}{\sqrt{1-x^{2}}}\)

⇒ -2xy² + (1 – x²) 2yy’ = 2y [∵ y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\)]
2y ஆல் இருபுறமும் வகுக்க’

-xy + (1 – x²)y’ = 1
x-ஐப் பொறுத்து மீண்டும் வகைப்படுத்த
⇒ -[xy’ + y(1)] + (1 – x²)y” + y'(-2x) = 0
⇒ -xy’ – y + (1 – x²)y” – 2xy” = 0
⇒ (1 – x²)y” – 3xy’ – y = 0
(1 – x²)y₂ – 3xy₁ – y = 0
எனவே நிருபிக்கப்பட்டது.

Question 26.
x = a(θ + sin θ), y = a(1 – cos θ) எனில், θ = \(\frac{pi}{2}\) மேலும் போது y” = \(\frac{1}{a}\) என நிரூபிக்க.
தீர்வு :
x = a(θ + sin θ)
⇒ \(\frac{d x}{d \theta}\) = a(1 + cosθ)
⇒ \(\frac{d x}{d \theta}\) = a(2 cos² \(\frac{\theta}{2}\)) [∵ y = e^tan-1]
மேலும் y = a(1 – cos θ)
⇒ \(\frac{d y}{d \theta}\) = a(sin θ) = 2a sin \(\frac{\theta}{2}\) cos \(\frac{\theta}{2}\)

∴ y’ = \(\frac{d y}{d x}\) = \(\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}\)
= \(\frac{2 a \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 a \cos ^{2} \frac{\theta}{2}}\)
= tan \(\frac{\theta}{2}\)

‘x’-ஐப் பொறுத்து மீண்டும் வகைப்படுத்த,

y” = sec² \(\frac{\theta}{2}\) . \(\frac{1}{2}\) . \(\frac{d \theta}{d x}\)

= sec² \(\frac{\theta}{2}\) . (\(\frac{1}{2}\)) . (\(\frac{1}{2 a \cos ^{2} \frac{\theta}{2}}\))

= \(\frac{1}{4 a} \sec ^{4} \frac{\theta}{2}\)

∴ θ = \(\frac{pi}{2}\) -ல்
y” = \(\frac{1}{4 a} \cdot\left[\sec \left(\frac{\pi}{4}\right)\right]^{4}\)
= \(\frac{1}{4 a}\) . (√2)⁴
= \(\frac{4}{4 a}\) = \(\frac{1}{a}\)
எனவே நிருபிக்கப்பட்டது.

Question 27.
siny = x sin(a + y) எனில், \(\frac{d y}{d x}\) = \(\frac{\sin ^{2}(a+y)}{\sin a}\) என் நிரூபிக்க. இங்கு a ≠ nπ.
தீர்வு :
sin y = x sin (a + y) ……………(1)
‘x’ ஐப் பொறுத்து வகைப்படுத்த
cos y \(\frac{d y}{d x}\) = x cos (a + y) \(\frac{d y}{d x}\) + sin (a + y) (1)
[பெருக்கல் விதிப்படி]
⇒ cos y \(\frac{d y}{d x}\) = x cos(a + y) \(\frac{d y}{d x}\) + sin (a + y)
⇒ \(\frac{d y}{d x}\) (cos y – x cos (a + y)) = sin (a +y)
⇒ \(\frac{d y}{d x}\) = \(\frac{\sin (a+y)}{\cos y-x \cos (a+y)}\)

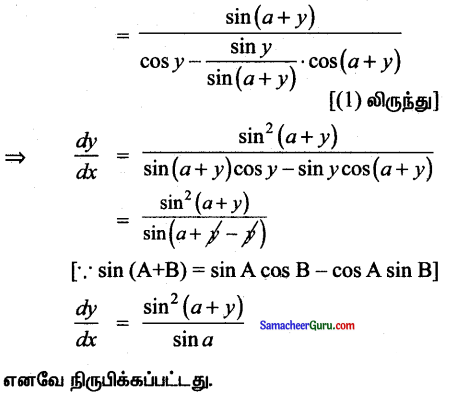
Question 28.
y= (cos^-1 x)² எனில், (1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – 2 = 0 என நிரூபிக்க. மேலும் x = 0-ன் போது y₂ மதிப்பைக் காண்க.
தீர்வு :
y = (cos^-1 x)²
‘x’-ஐப் பொறுத்து வகைப்படுத்த
y’ = 2. cos^-1 x. \(\frac{d}{d x}\) (cos^-1 x)

⇒ y’ = 2 . cos^-1 x \(\frac{-1}{\sqrt{1-x^{2}}}\) …………(1)

(y’)² \(\sqrt{1-x^{2}}\) = 4(cos^-1 x)²

இருபுறமும் வர்க்கப்படுத்த

(y’)² (1 – x²) = 4 (cos^-1 x)²

‘x’-ஐப் பொறுத்து மீண்டும் வகைப்படுத்த,

(y’)² (-2x) + (1 – x²) 2 y’ y” = 4(2) cos^-1 x . (cos^-1 x)
⇒ -2x(y’)² + 2(1 – x²)y’ . y” = 8 cos^-1 x .

= 8 cos^-1 x . \(\frac{-1}{\sqrt{1-x^{2}}}\)

⇒ -2x(y’)² + 2(1 – x²)y’ . y” = 4 \(\left(\frac{-2 \cos ^{-1} x}{\sqrt{1-x^{2}}}\right)\)

⇒ -2x(y’)² + 2(1 – x²)y’ . y” = 4 y’ [(1) லிருந்து]
2y ஆல் இருபுறமும் வகுக்க

⇒ -xy’ + (1 – x²) y” = 2
⇒ (1 – x²)y” – xy’ – 2 = 0
⇒அதாவது (1 – x²) \(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) – 2 = 0
எனவே நிருபிக்கப்பட்டது.