Samacheer Kalvi 11th Maths Guide Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 10 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 10.5 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 10 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 10.5

சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.

Question 1.
\(\frac{d}{d x}\left(\frac{2}{\pi} \sin x^{\circ}\right)\)

(1) \(\frac{\pi}{180}\) cos x°
(2) \(\frac{1}{90}\) cos x°
(3) \(\frac{\pi}{180}\) cos x°
(4) \(\frac{2}{\pi}\) cos x°
குறிப்பு :
\(\frac{d}{d x}\left(\frac{2}{\pi} \sin x^{\circ}\right)\) = \(\frac{2}{\pi}\) cos x°
= \(\frac{2}{180}\) cos x°
= \(\frac{1}{90}\) cos x°
விடை :
(2) \(\frac{1}{90}\) cos x°

Question 2.
y = f(x² + 2) மற்றும் f'(3) = 5 எனில், x = 1-ல் \(\frac{d}{d x}\) என்பது
(1) 5
(2) 25
(3) 15
(4) 10
குறிப்பு :
y = f(x² + 2)
y’ = f'(x² + 2) (2x)
⇒ f'(x² + 2) = \(\frac{y^{\prime}}{2 x}\) ……….(1)
f'(3) = 5 (1), (2)ஐ ஒப்பிட ……….(2)
x² + 2 = 3

⇒ x² = 1 ⇒ x = 1 மற்றும் \(\frac{y^{\prime}}{2 x}\) = 5
⇒ y’ = 10x
⇒ y = 10(1) = 10
விடை :
(4) 10

Question 3.
y = \(\frac{1}{4}\)u⁴, u = \(\frac{2}{3}\) x³ + 5 எனில், \(\frac{d y}{d x}\) என்பது
(1) \(\frac{1}{27}\) x² (2x³ + 15)³
(2) \(\frac{2}{27}\) x (2x³ + 5)³
(3) \(\frac{2}{27}\) x² (2x³ + 15)³
(4) \(-\frac{1}{27}\) x (2x³ + 5)³
குறிப்பு :
y = \(\frac{1}{4}\)u⁴ மற்றும் u = \(\frac{2}{3}\) x³ + 5 ……(1)
⇒ \(\frac{d y}{d u}\) = \(\frac{1}{90}\) × 4 u³
= u³ மற்றும்
\(\frac{d u}{d x}\) = \(\frac{2}{3}\) × 3x² = 2x²

∴ \(\frac{d y}{d x}\) = y’ = \(\frac{d y}{d u}\) × \(\frac{d u}{d x}\)

= u³ × 2x² = (\(\frac{2}{3}\) × x³ + 5) 2x²

= \(\frac{\left(2 x^{3}+15\right)^{3}}{3^{3}}\) × 2x²

= \(\frac{2}{27}\) x²(2x³ + 15)³
விடை :
(3) \(\frac{2}{27}\) x² (2x³ + 15)³

Question 4.
f (x) = x² – 3x எனில் , f (x) = f ‘(x) என அமையும் புள்ளிகள்
(1) இரண்டும் மிகை முழு எண்களாகும்
(2) இரண்டும் குறை முழு எண்களாகும்
(3) இரண்டுமே விகிதமுறா எண்களாகும்
(4) ஒன்று விகிதமுறு எண்ணாகவும் மற்றொன்று விகிதமுறா எண்ணாகவும் இருக்கும்.
குறிப்பு :
f(x) = x² – 3x
f’ (x) = 2x – 3
f(x) = f'(x)
x² – 3x = 2 – 3x
x² – 5x + 3 = 0
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

x = \(\frac{5 \pm \sqrt{25-12}}{2}=\frac{5 \pm \sqrt{13}}{2}\)
விடை :
(3) இரண்டுமே விகிதமுறா எண்களாகும்

Question 5.
y = \(\frac{1}{a-z}\) எனில், \(\frac{d z}{d y}\) -ன் மதிப்பு
(1) (a – z)²
(2) -(z – a)²
(3) (z + a)²
(4) -(z + a)²
குறிப்பு:
y = \(\frac{1}{a-z}\)

⇒ \(\frac{d y}{d z}\) = \(\frac{1}{(a-z)^{2}}\)
⇒ \(\frac{d z}{d y}\) = (a – z)²
விடை :
(1) (a – z)²

Question 6.
y = cos (sin x²) எனில், x = \(\sqrt{\frac{\pi}{2}}\) -உஅ மதிப்பு
(1) -2
(2) 2
(3) -2\(\sqrt{\frac{\pi}{2}}\)
(4) 0
குறிப்பு :
y = cos (sin x²)
2 = – sin (sin x²). \(\frac{d}{d x}\)(sin x²)
= – sin (sin x²) . cos x² . \(\frac{d}{d x}\)(2x)
= – sin (sin x²) . cos x² . 2
= – 2 sin (sin x²) . cos x²
x = \(\sqrt{\frac{\pi}{2}}\)
\(\frac{d y}{d x}\) = -2 sin (sin \(\frac{pi}{2}\)) cos \(\frac{pi}{2}\)
= – 2 (sin 1) × 0 = 0
விடை :
(4) 0

Question 7.
y = mx + c மற்றும் f (0) = f'(0) = 1 எனில், f (2) என்பது
(1) 1
(2) 2
(3) 3
(4) -3
குறிப்பு :
y = mx + c
y’ = m ⇒ f’ (0) = m
f(0) = c
f(0) = f’ (0) = 1 m = c = 1
∴ y = x + 1
⇒ f(2) = (2) = 2 + 1 = 3
விடை :
(3) 3

Question 8.
f (x) = x tan^-1x எனில், f'(1) என்பது
(1) 1 + \(\frac{\pi}{4}\)
(2) \(\frac{1}{2}\) + \(\frac{\pi}{4}\)
(3) \(\frac{1}{2}\) – \(\frac{\pi}{4}\)
(4) 2
குறிப்பு :
f (x) = x tan^-1 x
f'(x) = x . \(\frac{1}{1+x^{2}}\) + tan^-1 x
f'(1) = 1\(\left(\frac{1}{1+1}\right)\) + tan^-1 (1)
= \(\frac{1}{2}\) + \(\frac{pi}{4}\)
விடை :
(2) \(\frac{1}{2}\) + \(\frac{\pi}{4}\)

Question 9.
\(\frac{d}{d x}\) (e^{x + 5 log x}) என்பது
(1) e^x . x⁴ (x + 5)
(2) e^x . x(x + 5)
(3) e^x + \(\frac{5}{x}\)
(4) e^x – \(\frac{5}{x}\)
குறிப்பு:
\(\frac{d}{d x}\) (e^{x + 5 log x}) = \(\frac{d}{d x}\) (e^{x + log x5})

= \(\frac{d}{d x}\)(e^x . e^{log x5})
= \(\frac{d}{d x}\)(e^x . x⁵)
= e^x . 5x⁴ + x⁵ . e^x [பெருக்கல் விதிப்படி)
= e^x . x⁴(5 + x)
விடை :
(1) e^x . x⁴ (x + 5)

Question 10.
x = 0-ல் (ax – 5)e^3x -ன் வகைக்கெழு -13 எனில், ‘a’-ன் மதிப்பு
(1) 8
(2) -2
(3) 5
(4) 2
குறிப்பு :
(\(\frac{d}{d x}\)(ax – 5) e^3x) = (ax – 5) e^3x (3) + e^3x (a)
x = 0-ல் -13 = -15 (e⁰) + ae⁰
= -15 + a
-15 + a = -13
⇒ a =-13 + 15 = a= 2
விடை :
(4) 2

Question 11.
x = \(\frac{1-t^{2}}{1+t^{2}}\), y = \(\frac{2 t}{1+t^{2}}\) எனில், \(\frac{d y}{d x}\) என்பது
(1) –\(\frac{y}{x}\)
(2) \(\frac{y}{x}\)
(3) –\(\frac{x}{y}\)
(4) \(\frac{x}{y}\)
குறிப்பு :

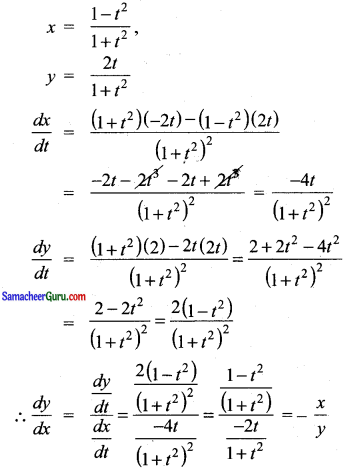
விடை :
(3) –\(\frac{x}{y}\)

Question 12.
x = a sin θ மற்றும் y = b cos θ எனில், 4\(\frac{d^{2} y}{d x^{2}}\) என்பது
(1) \(\frac{a}{b^{2}}\) sec² θ
(2) – \(\frac{b}{a}\) sec² θ
(3) \(-\frac{b}{a^{2}}\) sec³ θ
(4) \(-\frac{b^{2}}{a^{2}}\) sec³ θ
குறிப்பு :
x = a sin θ மற்றும் y = b cos θ

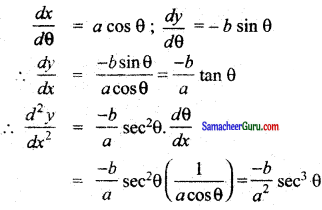
விடை :
(3) \(-\frac{b}{a^{2}}\) sec³ θ

Question 13.
log_x 10-ஐ பொறுத்து log₁₀ x -ன் வகைக்கெழு
(1) 1
(2) -(log₁₀ x)²
(3) (log_x 10)²
(4) \(\frac{x^{2}}{100}\)
குறிப்பு :
u = log₁₀ x,
v = log_x 10

விடை :
(2) -(log₁₀ x)²

Question 14.
f(x) = x + 2 எனில், x = 4. f'(f(x))-ன் மதிப்பு
(1) 8
(2) 1
(3) 4
(4) 5
குறிப்பு :
f(x) = x + 2
f'(f(x)) = f'(x + 2) = 1
விடை :
(2) 1

Question 15.
y = \(\frac{(1-x)^{2}}{x^{2}}\) எனில், \(\frac{d y}{d x}\) -ன் மதிப்பு
(1) \(\frac{2}{x^{2}}+\frac{2}{x^{3}}\)

(2) \(-\frac{2}{x^{2}}+\frac{2}{x^{3}}\)

(3) \(-\frac{2}{x^{2}}-\frac{2}{x^{3}}\)

(4) \(-\frac{2}{x^{3}}+\frac{2}{x^{2}}\)
குறிப்பு :
\(\frac{d y}{d x}\) = \(\frac{x^{2} \cdot 2(1-x)(-1)-(1-x)^{2} \cdot 2 x}{x^{4}}\)

Question 16.
pv = 81 எனில், v = 9-ல் \(\frac{d p}{d v}\)-“உன் மதிப்பு
(1) 1
(2) – 1
(3) 2
(4) -2
குறிப்பு :
pv = 81
⇒ p = \(\frac{81}{v}\)
⇒ \frac{d p}{d v}=\frac{-81}{v^{2}}
v = 9-ல்
\(\frac{d p}{d v}=\frac{-81}{81}\) = -1
விடை :
(2) -1

Question 17.
f(x) = \(\left\{\begin{array}{rr}
x-5 & , \quad x \leq 1 \\
4 x^{2}-9 & , \quad 1<x<2 \\
3 x+4, & x \geq 2
\end{array}\right.\) எனில், x = 2-ல் f(x)-ன் வலப்பக்க வகைக்கெழு
(1) 0
(2) 2
(3) 3
(4) 4
குறிப்பு :

(விடை :
(3) 1

Question 18.
f'(a) உள்ளது எனில், \(\lim _{x \rightarrow a} \frac{x f(a)-a f(x)}{x-a}\) ல்ள்பதி
(1) f (a) – af'(a)
(2) f'(a)
(3) -f'(a)
(4) f (a) + af'(a)
குறிப்பு :
\(\lim _{x \rightarrow a} \frac{x f(a)-a f(x)}{x-a}\)

f'(a) = \(\lim _{x \rightarrow a} \frac{a f(x)-a f(a)}{x-a}\)
⇒ af'(a) = \(\lim _{x \rightarrow a} \frac{a f(x)-a f(a)}{x-a}\)

∴ f(a) – f'(a) = f(a) – \(\lim _{x \rightarrow a} \frac{a f(x)-a f(a)}{x-a}\)

∴ f(a) – f'(a) = \(\lim _{x \rightarrow a}\) f(a) – \(\frac{a f(x)-a f(a)}{x-a}\)

= \(\lim _{x \rightarrow a} \frac{x f(a)-a f(a)-a f(x)+a f(a)}{x-a}\)

= \(\lim _{x \rightarrow a} \frac{x f(a)-a f(x)}{x-a}\)
[விடை :
(1) f (a) – af'(a)

Question 19.
f(x) = \(\left\{\begin{array}{cl}
x+1, & x<2 \\
2 x-1 & x \geq 2
\end{array}\right.\), எனில் எனில், f'(2) என்பது
(1) 0
(2) 1
(3) 2
(4) கிடைக்கப்பெறாது
குறிப்பு :
f(x) = \(\left\{\begin{array}{cl}
x+1, & x<2 \\
2 x-1 & x \geq 2
\end{array}\right.\)
குறிப்பு :

விடை :
(4) கிடைக்கப்பெறாது

Question 20.
g(x) = (x² + 2x + 3) f(x), f(0) = 5 மற்றும் \(\lim _{x \rightarrow \infty} \frac{f(x)-5}{x}\) = 4 எனில்,g ‘(0) என்பது
(1) 20
(2) 14
(3) 18
(4) 12
விடை :
(2) 14

Question 21.
f(x) = \(\left\{\begin{array}{rr}
x+2 & -1<x<3 \\ 5 & x=3 \\ 8-x & x>3
\end{array}\right.\) x = 3ல் f'(x) என்பது 18-x x>3
(1) 1
(2) -1
(3) 0
(4) கிடைக்கப்பெறாது
குறிப்பு :
f(x) = \(\left\{\begin{array}{rr}
x+2 & -1<x<3 \\ 5 & x=3 \\ 8-x & x>3
\end{array}\right.\)

[∵ f(x) = 8 – x; f(3) = 5]

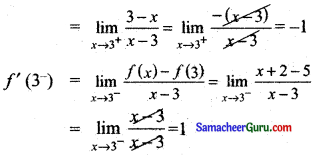
∴ f'(3⁺) ≠ f'(3^–)
∴ f’ (x) ஆனது x = 3-ல் கிடைக்கப்பெறாது
விடை :
(4) கிடைக்கப்பெறாது

Question 22.
x = -3-ல் f(x) = x|x| – ன் வகையிடலின் மதிப்பு
(1) 6
(2) -6
(3) கிடைக்கப்பெறாது.
(4) 0
குறிப்பு :
f(x) = x|x| = x², x ≥ 0 = -x², x < 0
f'(3⁺) = \(\lim _{x \rightarrow-3^{+}} \frac{f(x)-f(3)}{x-3}\)

= \(\lim _{x \rightarrow-3^{+}} \frac{x^{2}-9}{x-3}\)

= \(\lim _{x \rightarrow-3^{+}} \frac{(x+3)(x-3)}{x-3}\)

= 3 + 3 = 6
(விடை :
(1) 6

Question 23.
f(x) = \(\left\{\begin{array}{lr}
2 a-x, & -a<x<a \\
3 x-2 a & x \geq a
\end{array}\right.\) எனில் கீழ்க்காணும் கூற்றுகளில் எது மெய்யானது?
(1) x = a-ல் f(x) வகைமை இல்லை
(2) x= a-ல் f (x) தொடர்ச்சியற்று உள்ளது
(3) R-ல் உள்ள X-க்கும் f (x) தொடர்ச்சியானது.
(4) அனைத்து x ≥ a-க்கும் f(x) வகைமையாகிறது
குறிப்பு :
f(x) = \(\left\{\begin{array}{lr}
2 a-x, & -a<x<a \\
3 x-2 a & x \geq a
\end{array}\right.\)

விடை :
(1) x = a-ல் f (x) வகைமை இல்லை

Question 24.
f(x) = \(\left\{\begin{array}{cl}
x^{2}-b, & -1<x<1 \\
\frac{1}{|x|}
\end{array}\right.\) x = 1-ல் வகைமையாகிறது என்பதால்
(1) a = \(\frac{1}{2}\), b = –\(\frac{3}{2}\)
(2) a = \(-\frac{1}{2}\), b = \(\frac{1}{2}\)
(3) a = \(-\frac{1}{2}\), b = \(-\frac{3}{2}\)
(4) a = \(\frac{1}{2}\), b = \(\frac{3}{2}\)
குறிப்பு :
f(x) = \(\left\{\begin{array}{cl}
x^{2}-b, & -1<x<1 \\
\frac{1}{|x|} & பிற
\end{array}\right.\)
f(x) ஆனது x = 1-ல் வகைமையாகிறது என்பதால்
f'(1⁺) = f ‘(¹)

\(\lim _{x \rightarrow 1^{+}} \frac{f(x)-f(1)}{x-1}=\lim _{x \rightarrow 1^{-}} \frac{f(x)-f(1)}{x-1}\)

⇒ \(\lim _{x \rightarrow 1^{+}} \frac{\frac{1}{|x|}-1}{x-1}=\lim _{x \rightarrow 1^{-}} \frac{a x^{2}-b-1}{x-1}\)

⇒ \(\frac{1-1}{x-1}=\lim _{x \rightarrow 1^{-}} \frac{a x^{2}-b-1}{x-1}\)

⇒ a – b – 1 = 0
⇒ a – b = 1

a = \(-\frac{1}{2}\), b = \(-\frac{3}{2}\) ஆனது

a – b = 1 ஐ பூர்த்தி செய்கிறது.

விடை :
(3) \(-\frac{1}{2}\), b = \(-\frac{1}{2}\)

Question 25.
f(x) = |x – 1| + |x – 3 | + sin x எனும் சார்பு R ல் வகைமையாகாத புள்ளிகளின் எண்ணிக்கை
(1) 3
(2) 2
(3) 1
(4) 4
குறிப்பு:
f(x) = |x – 1|+ |x – 3| + sin x ஆனது
x = 1, x = 3-ல் வகைமை ஆகாது. ஏனெனில்
x = 1, x = 3-ல் f(x)க்கு செங்குத்து தொடுகோடு உண்டு…
விடை :
(2) 21