Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 11 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 11.10 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.10
சன் வற்றைத் தொகையிடுக.
Question 1.
\(\frac{1}{4-x^{2}}\)
தீர்வு :
I = ∫ \(\frac{1}{4-x^{2}}\) dx
= ∫ \(\frac{1}{2^{2}-x^{2}}\) dx என்க
∴ I = \(\frac{1}{2 \times 2} \log \left|\frac{2+x}{2-x}\right|\) + c
I = \(\frac{1}{4} \log \left|\frac{2+x}{2-x}\right|\) + c
(ii) \(\frac{1}{25-4 x^{2}}\)
I = ∫ \(\frac{1}{25-4 x^{2}}\) dx
= ∫ \(\frac{d x}{5^{2}-(2 x)^{2}}\) என்க
t = 2x என்க
⇒ dt = 2 dx
⇒ \(\frac{d t}{2}\) = dx
∴ I = \(\frac{1}{2}\) ∫ \(\frac{d t}{5^{2}-t^{2}}\)
= \(\frac{1}{2}\) × \(\frac{1}{2 \times 5} \log \left|\frac{5+t}{5-t}\right|\) + c
= \(\frac{1}{20} \log \left|\frac{5+2 x}{5-2 x}\right|\) + c [∵ t = 2x]
(iii) \(\frac{1}{9 x^{2}-4}\)
தீர்வு :
I = ∫ \(\frac{1}{9 x^{2}-4}\) dx
= ∫ \(\frac{d x}{(3 x)^{2}-2^{2}}\) என்க
t = 3x ⇒ \(\frac{d t}{3}\) = dx என்க
∴ I = \(\frac{1}{3}\) ∫ \(\frac{d t}{t^{2}-2^{2}}\)
\(\int \frac{d x}{x^{2}-a^{2}}=\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|+c\)∴ I = \(\frac{1}{3} \times \frac{1}{2 \times 2} \log \left|\frac{t-2}{t+2}\right|\) + c
= \(\frac{1}{12} \log \left|\frac{3 x-2}{3 x+2}\right|\) + c [∵ t = 3x]
![]()
Question 2.
(i) \(\frac{1}{6 x-7-x^{2}}\)
(ii) \(\frac{1}{(x+1)^{2}-25}\)
(iii) \(\frac{1}{\sqrt{x^{2}+4 x+2}}\)
தீர்வு :
I = ∫ \(\frac{1}{6 x-7-x^{2}}\) dx
= -∫ \(\frac{d x}{x^{2}-6 x+7}\)
I = – ∫ \(\frac{d x}{x^{2}-6 x+9-9+7}\)

(ii) \(\frac{1}{(x+1)^{2}-25}\)
தீர்வு :
I = ∫ \(\frac{d x}{(x+1)^{2}-25}\)
= ∫ \(\frac{d x}{(x+1)^{2}-5^{2}}\) என்க
t = x + 1 ⇒ dt = dx என்க
∴ I = ∫ \(\frac{d t}{t^{2}-5^{2}}\)
= \(\frac{1}{2 \times 5} \log \left|\frac{t-5}{t+5}\right|\) + c
= \(\frac{1}{10} \log \left|\frac{x+1-5}{x+1+5}\right|\) + c
I = \(\frac{1}{10} \log \left|\frac{x-4}{x+6}\right|\) + c
(iii) \(\frac{1}{\sqrt{x^{2}+4 x+2}}\)
தீர்வு :
I = ∫ \(\frac{1}{\sqrt{x^{2}+4 x+2}}\)
= ∫ \(\frac{d x}{\sqrt{x^{2}+4 x+4-4+2}}\)
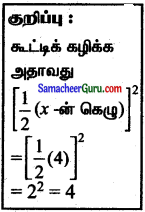
= ∫ \(\frac{d x}{\sqrt{(x+2)^{2}-2}}\)
= ∫ \(\frac{d x}{\sqrt{(x+2)^{2}-(\sqrt{2})^{2}}}\)
∫ \(\frac{d x}{\sqrt{x^{2}-a^{2}}}\) = log |x + \(\sqrt{x^{2}-a^{2}}\)| + c
I = log |x + 2 + \(\sqrt{x^{2}+4 x+2}\)| + c
![]()
Question 3.
(i) \(\frac{1}{\sqrt{(2+x)^{2}-1}}\)
(ii) \(\frac{1}{\sqrt{x^{2}-4 x+5}}\)
(iii) \(\frac{1}{\sqrt{9+8 x-x^{2}}}\)
தீர்வு :
(i) \(\frac{1}{\sqrt{(2+x)^{2}-1}}\)
I = ∫ \(\frac{1}{\sqrt{(2+x)^{2}-1}}\) dx
= ∫ \(\frac{1}{\sqrt{(x+2)^{2}-1}}\) dx
[∵ ∫ \(\frac{d x}{\sqrt{x^{2}-a^{2}}}\) = \(\frac{1}{2a}\) log |x + \(\frac{d x}{\sqrt{x^{2}-a^{2}}}\)| + c
= \(\frac{1}{2}\) [log(x + 2) + \(\sqrt{(x+2)^{2}}\) – 1| + c
(ii) \(\frac{1}{\sqrt{x^{2}-4 x+5}}\)
I = ∫ \(\frac{1}{\sqrt{x^{2}-4 x+5}}\) dx
= ∫ \(\frac{d x}{\sqrt{x^{2}-4 x+4-4+5}}\)
= ∫ \(\frac{d x}{\sqrt{(x-2)^{2}+1^{2}}}\)
\(\int \frac{d x}{\sqrt{x^{2}+a^{2}}}\) = log |x + \(\sqrt{x^{2}+a^{2}}\)|
I = log |x – 2 + \(\sqrt{x^{2}-4 x+5}\)|
(iii) \(\frac{1}{\sqrt{9+8 x-x^{2}}}\)
தீர்வு :
I = ∫ \(\frac{1}{\sqrt{9+8 x-x^{2}}}\) dx
= ∫ \(\int \frac{d x}{\sqrt{-\left(x^{2}-8 x+16-16\right.}}\)
= ∫ \(\frac{d x}{\sqrt{-\left[(x-4)^{2}-25\right]}}\)
= ∫ \(\frac{d x}{\sqrt{25-(x-4)^{2}}}\)
= ∫ \(\frac{d x}{\sqrt{5^{2}-(x-4)^{2}}}\)
∫ \(\frac{d x}{\sqrt{a^{2}-x^{2}}}\) = sin-1 \(\left(\frac{x}{a}\right)\)
I = sin-1 \(\left(\frac{x-4}{5}\right)\) + c