Samacheer Kalvi 11th Maths Guide Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 11 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 11.4 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.4

Question 1.
f'(x) = 4x – 5 மற்றும் f(2) = 1 எனில், f(x) காண்க.
தீர்வு :
f'(x) = 4x – 5
f(2) = 1
இருபுறமும் தொகையீடு காண
∫ f'(x) = ∫(4x – 5) dx
f(x) = 4 ∫ xdx – 5 ∫ dx = 4 . \(\frac{x^{2}}{2}\) – 5x + c
f(x) = 2x² – 5x + c …………(1)
f(2) = 1
⇒ f(2) = 2(2)² – 5(2) + c
⇒ 1 = 8 – 10 + c
⇒ 1 = – 2 + c
⇒ c = 3
c = 3 என (1)-ல் பிரதியிட,
f(x) = 2x² – 5x + 3

Question 2.
f'(x) = 9x² – 6x மற்றும் f(0) = -3 எனில் f (x) காண்க.
தீர்வு :
f'(x) = 9x² – 6
f(0) = -3
இருபுறமும் தொகையீடு காண
∫ f'(x) dx = ∫ 9x² – 6x dx
f(x) =9 ∫ x² – 6 ∫ x dx
f(x) =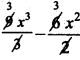+ c
= 3x³ – 3x² + c …………. (1)
fo) = -3 என்பதால்
⇒ f(0) = 3(0) – 3(0) + c
⇒ c = -3
c = – 3 என (1)-ல் பிரதியிட
f(x) = 3x³ – 3x² – 3
f(x) = 3(x³ – x² – 1)

Question 3.
f”(x) = 12x – 6 மற்றும் f(1) = 30, f'(1) = 5 எனில் f(x) காண்க.
தீர்வு :
f”(x) = 12x – 6
f(1) = 30
f'(1) = 5
இருபுறமும் தொகையீடு காண
∫ f”(x) = ∫ (12x – 6) dx
⇒ f'(x) = 12 ∫ x dx – 6 ∫ dx = \(\frac{12 x^{2}}{2}\) – 6x + c
f'(x) = 6x² – 6x + c
f'(1) = 5 என்பதால்
⇒ f'(1) = 6(1)² – 6(1) + c
⇒ 5 = 6 – 6 + c
c = 5
∴ f'(x) = 6x² – 6x + c [(1) லிருந்து]
x – ஐப் பொறுத்து மீண்டும் தொகையீடு காண
∫ f'(x) = ∫ (6x² – 6x + 5) dx
= 6 ∫ x² dx – 6 ∫ x dx + 5 ∫ dx
⇒ f(x) =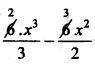+ 5x + k ………… (2)
f(1) = 30 என்பதால்
f(1) = 2(1)³ – 3(1)² + 5(1) + k
⇒ 30 = 2 – 3 + 5 + k
⇒ 30 = 4 + k
∴ k = 26
k = 26 என (2)-ல் பிரதியிட
f (x) = 2x³ – 3x² + 5x + 26

Question 4.
ஒரு பந்து 39.2 மீ/வினாடி ஆரம்பதிசை வேகத்தில் தரையிலிருந்து மேல் நோக்கி எறியப்படுகிறது. இங்கு முடுக்கத்தை ஈர்ப்பு விசையைப் பொறுத்து மட்டும் கருதும் போது (அ) எவ்வளவு நேரம் கழித்துப் பந்து தரையை வந்து மோதும்? (ஆ) எந்த வேகத்தில் பந்தானது தரையை மோதும்? (இ) பந்தானது எவ்வளவு தூரம் மேல் நோக்கிச் செல்லும் என்பதனைக் காண்க.
தீர்வு :
ஆரம்ப திசை வேகம் u = 39.2 மீ/வினாடி.
தொலைவு d = ut – \(\frac{1}{2}\)gt²,
g = 9.8 மீ/வினாடி
⇒ x = 39.2t – \(\frac{1}{2}\)(9.8)t²
∴ x = 39.2t – 4.9t² …. (1)
(அ) பந்து தரையை மோத, x = 0
⇒ 39.2t – 4.9t² = 0
⇒ 39.2t = 4.9t² [∵ t ≠ 0]
t = \(\frac{39.2}{4.9}\)
∴ t = 8 வினாடி
(ஆ) பந்து தரையை மோதும் போது உள்ள வேகம்
t = 8 வினாடி
x = 39.21 – 4.9
dx = 39.2t – 4.9(2t)
t = 8 வினாடி
v = 39.2 – 9.8 (8)
= 39.2 – 78.4
= – 39.2 மீ/வினாடி.
திசைவேகம் குறையெண்ணாக இருக்க முடியாது.
ஆதலால் v = 39.2 மீ/வினாடி
(இ) பந்து மேல்நோக்கி செல்லும் உயரம் காண v = 0
39.2 – 9.8t = 0
39.2 = 9.8t
t = \(\frac{39.2}{9.8}\) = 4 வினாடி
அதிகபட்ச உயரம் x = 39.2(4) – 4.9 (16)
[(1) லிருந்து)]
= 156.8 – 78.4 = 18.4 மீ

Question 5.
ஒருவருக்கு ஏற்பட்ட காயம் ஆனது \(-\frac{6}{(t+2)^{2}}\) செ.மீ2 0 < t < 8 நாள் என்ற வீதத்தில் ஞாயிற்றுக்கிழமை முதல் குணமடையத் தொடங்குகிறது. திங்கட்கிழமை அன்று காயப்பகுதியின் பரப்பு 1.4 செ.மீ2 எனில் (இங்கு என்பது நாட்களைக் குறிக்கிறது)
(அ) ஞாயிற்றுக்கிழமையன்று காயப்பகுதியின் பரப்பளவு எவ்வளவாக இருந்திருக்கும்? –
(ஆ) இதே வீதத்தில் தொடர்ந்து குணமாகிக் கொண்டிருக்கும் போது வியாழக்கிழமையன்று எதிர்பார்க்கும் காயப் பகுதியின் பரப்பு எவ்வளவு?
தர்வு :
ஞாயிற்றுக்கிழமையை துவக்க நாளாகக் கொள்வோம்.

\(\frac{d A}{d t}=\frac{-6}{(t+2)^{2}}\) கொடுக்கப்பட்டுள்ளது.

(இங்கு A என்பது காயத்தின் பரப்பு]

⇒ dA = -6(t + 2)^-2 dt

இருபக்கமும் தொகை காண கிடைப்பது,
∫ dA = -6 ∫ (t + 2)^-2 dt

⇒ A = -6 \(\frac{(t+2)^{-2+1}}{-2+1}\) + c

⇒ A = -6 \(-6 \frac{(t+2)^{-1}}{-1}\) + c

⇒ A = \(\frac{6}{t+2}\) + c ………..(1)

t = 1 எனில் A = 1.4 செ.மீ2 என கொடுக்கப்பட்டுள்ளது.
(ஞாயிற்றுக்கிழமையிலிருந்து திங்கட்கிழமை என்பது ஒரு நாள் ∴ t = 1]

⇒ 1.4 = \(\frac{6}{1+2}\) + c
⇒ 1.4 = \(\frac{6}{3}\) + c
⇒ 1.4 = 2 + c ⇒ c = 1.4 – 2
⇒ c = -0.6
∴ சமன்பாடு (1)
A = – \(\frac{6}{t+2}\) – 0.6 என்றாகிறது ………… (2)

(i) ஞாயிற்றுகிழமையன்று காயப்பகுதி பரப்பளவைக் காண t = 0 என (2)ல் பிரதியிட
∴ A = \(\frac{6}{0+2}\) – 0.6
= \(\frac{6}{2}\) – 0.6 = 3 – 0.6
A = 2.4 சதுர செ.மீ
∴ ஞாயிற்றுக்கிழமையன்று காயப்பகுதியில் பரப்பு 2.4 சதுர செ.மீ.

(ii) வியாழக்கிழமையன்று எதிர்பார்க்கும் பரப்பளவு காண t = 4 என (2)ல் பிரதியிட்டால்
[∵ ஞாயிற்றுக்கிழமையிலிருந்து வியாழக்கிழமை வரை 4 நாட்கள்]
∴ t = 4 எனில் சமன்பாடு (2)
A = \(\frac{6}{2+4}\) – 0.6 = \(\frac{6}{6}\) – 0.6 = 1 – 0.6 = 0.4
சதுர செ.மீ எனவே வியாழக்கிழமை எதிர்பார்க்கப்படும் காயப்பகுதியின் பரப்பளவு 0.4 சதுர செ.மீ.