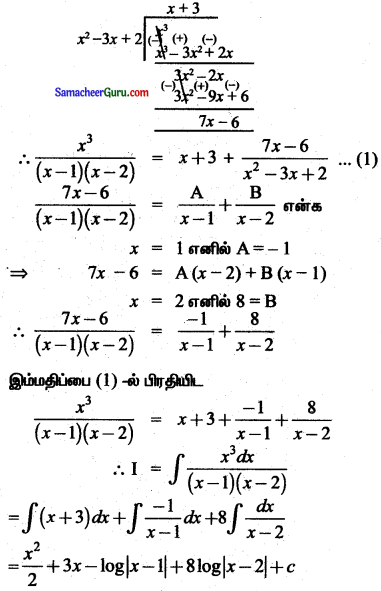Samacheer Kalvi 11th Maths Guide Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 11 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 11.5 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.5

கீழ்க்காண்பவற்றைத் தொகையிடுக.

Question 1.
\(\frac{x^{3}+4 x^{2}-3 x+2}{x^{2}}\)
தீர்வு :
∫ (\(\frac{x^{3}+4 x^{2}-3 x+2}{x^{2}}\)) dx

= ∫ \(\left(\frac{x^{3}}{x^{2}}+\frac{4 x^{2}}{x^{2}}-\frac{3 x}{x^{2}}+\frac{2}{x^{2}}\right)\) dx

= ∫ (x + 4 – \(\frac{3}{x}\) + \(\frac{2}{x^{2}}\)) dx

= ∫ x dx + 4 ∫ dx – 3 ∫ \(\frac{1}{x}\) dx + 2 ∫ \(\frac{1}{x^{2}}\) dx

= \(\frac{x^{2}}{2}\) + 4x – 3 log|x| + 2 ∫ x^-2 dx + c

= \(\frac{x^{2}}{2}\) + 4x – 3 log|x| + 2\(\frac{x^{-1}}{-2+1}\) + c

= \(\frac{x^{2}}{2}\) + 4x – 3 log|x| – \(\frac{2}{x}\) + c

Question 2.
\(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\)
தீர்வு :
∫ \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\) dx = ∫ (x + \(\frac{1}{x}\) + 2 . √x . \(\frac{1}{\sqrt{x}}\) ) dx

= ∫ (x + \(\frac{1}{x}\) + 2)dx
= ∫ x dx + ∫ \(\frac{1}{x}\) dx + 2 ∫ dx
= \(\frac{x^{2}}{2}\) + log|x| + 2x + c

Question 3.
(2x -5) (36 + 4x)
தீர்வு :
∫ (2x -5) (36 + 4x) dx = ∫ (72x + 8x² – 180 – 20x)dx
= ∫ (8x² + 52x – 180) dx
= 8 ∫ x² dx + 52 ∫ xdx – 180 ∫ dx
= \(\frac{8 x^{3}}{3}+\frac{52 x^{2}}{2}\) – 180x + cos

= \(\frac{8 x^{3}}{3}\) + 26x² – 180x + c

Question 4.
cot² x + tan² x
தீர்வு :
∫ (cot² x + tan² x) dx

= ∫ (cosec² x – 1 + sec² x – 1) dx
[∵ 1 + tan² x = sec² x, 1 + cot² x = cosec² x]

= ∫ (cosec² x + sec² x – 2) dx

= ∫ cosec² x dx + ∫ sec² x dx – 2 ∫ dx

= – cot x + tan x – 2x + c

= tan x – cot x – 2x + c

Question 5.
\(\frac{\cos 2 x-\cos 2 \alpha}{\cos x-\cos \alpha}\)
தீர்வு :
∫ \(\frac{2 \cos ^{2} x-1-\left(2 \cos ^{2} \propto-1\right)}{\cos x-\cos \propto}\) dx
[∵ cos 2θ = cos² θ – 1]

=

= 2 ∫ (cos x + cos ∝) dx = 2 [ ∫ cos x dx + cos ∝ ∫ dx]
= 2[sin x + x cos ∝] + c
= 2[sin x + x cos ∝] + c

Question 6.
\(\frac{\cos 2 x}{\sin ^{2} x \cos ^{2} x}\)
தீர்வு :
∫ \(\frac{\cos 2 x}{\sin ^{2} x \cos ^{2} x}\) dx

4 ஆல் பெருக்கி 4 ஆல் வகுக்க 4f_cos 2x

= 4 ∫ \(\frac{\cos 2 x}{4 \sin ^{2} x \cos ^{2} x}\)

= 4 ∫ \(\frac{\cos 2 x}{(2 \sin x \cos x)^{2}}\) dx

= 4 ∫ \(\frac{\cos 2 x}{(\sin 2 x)^{2}}\) dx [∵ sin 2x = 2 sin x cos x]

= 4 ∫ \(\frac{\cos 2 x}{\sin 2 x} \cdot \frac{1}{\sin 2 x}\) dx

= 4 ∫ cot 2x . cosec 2x dx

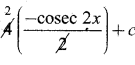= = -2 cosec 2x + c

Question 7.
\(\frac{3+4 \cos x}{\sin ^{2} x}\)
தீர்வு :
∫ \(\frac{3+4 \cos x}{\sin ^{2} x}\) dx
= ∫ \(\frac{3}{\sin ^{2} x}\) dx + ∫ \(\frac{4 \cos x}{\sin ^{2} x}\) dx

= 3 ∫ cosec² x dx + 4 ∫ \(\frac{\cos x}{\sin x} \times \frac{1}{\sin x}\) dx

= 3(-cot x) + 4 ∫ cot x cosec x dx + c

= -3 cot x + 4 (cosec x) + c

Question 8.
\(\frac{\sin ^{2} x}{1+\cos x}\)
தீர்வு :
∫ \(\frac{\sin ^{2} x}{1+\cos x}\) dx

= ∫ \(\frac{\left(1-\cos ^{2} x\right)}{1+\cos x}\) dx
[∵ sin² x + cos² x = 1]

= 2 ∫ \(\frac{(1+\cos x)(1-\cos x)}{1+\cos x}\) dx = ∫ (1 – cos x) dx

= ∫ dx – ∫ cos dx = x – sin x + c

Question 9.
\(\frac{\sin 4 x}{\sin x}\)
தீர்வு :
∫ \(\frac{\sin 4 x}{\sin x}\) dx = ∫ 2 \(\frac{\sin 2 x \cdot \cos 2 x}{\sin x}\) dx
[∵ sin 4x = 2 sin 2x cos 2x]

= 2 ∫ \(\frac{2 \sin x \cos x \cdot \cos 2 x}{\sin x}\) dx
[∵ sin 2x = 2 sin x cos x]

= 2 ∫ 2 cos x cos 2x dx
= 2 ∫ [cos(x + 2x) + cos(x – 2x)] dx
[∵ 2 cos A cos B = cos(A + B) + cos(A – B)]
= 2 ∫ cos 3x + cos (-x) dx
= 2 ∫cos 3x dx + ∫ cos x dx
= 2[\(\frac{\sin 3 x}{3}\) + sin x] + c

Question 10.
cos 3x cos 2x.
தீர்வு :
I = ∫ cos3x cos 2x dx என்க.
2 ஆல் பெருக்கி 2 ஆல் வகுக்க
I = \(\frac{1}{2}\) ∫ 2cos 3x cos 2x dx
= \(\frac{1}{2}\) ∫ cos(3x + 2x) + cos(3x – 2x)dx
[∵ 2cosA cosB = cos (A + B) + cos (A – B)]
= \(\frac{1}{2}\) ∫ cos 5x dx + cos x dx
= \(\frac{1}{2}\) [ ∫ cos 5x dx + ∫ cos x dx]
= \(\frac{1}{2}\) [\(\frac{\sin 5 x}{5}\) + sin x] + c

Question 11.
sin² 5x
தீர்வு :
∫ sin² 5x = \(\frac{1}{2}\) ∫ 1 – cos 2(5x) dx
[∵ cos 2x = 1 – 2 sin² x
⇒ sin² x = \(\frac{1}{2}\) (1 – cos 2x)]
= \(\frac{1}{2}\) [∫ (1 – cos 10x) dx] = \(\frac{1}{2}\) [∫ dx – ∫ cos 10x dx]
= \(\frac{1}{2}\) [x – \(\frac{\sin 10 x}{10}\)] + c

Question 12.
\(\frac{1+\cos 4 x}{\cot x-\tan x}\)
தீர்வு :

= ∫ sin 2x . cos 2x dx
2 ஆல் பெருக்கி வகுக்க
1 = \(\frac{1}{2}\) ∫ 2 sin 2x cos 2x dx
= \(\frac{1}{2}\) ∫ sin 4x dx
= \(\frac{1}{2}\) [- \(\frac{\cos 4 x}{4}\)] + c
= \(\frac{1}{8}\) cos 4x + c

Question 13.
e^{x log a} e^x
தீர்வு :
I = ∫ e^{x log a} . e^x . dx
= ∫ e ^{log ax} . e^x dx
= ∫ a^x × e^x dx
= ∫ (ae)^x dx [∵ e^{log x} = x]
= \(\frac{(a e)^{x}}{\log (a e)}\) + c
[∫ a^x dx = \(\frac{a^{x}}{\log a}\) + c]

Question 14.
(3x + 4)\(\sqrt{3 x+7}\)
தீர்வு :
I = ∫ (3x + 4)\(\sqrt{3 x+7}\) dx என்க
= ∫ (3x + 7 – 3) \(\sqrt{3 x+7}\) dx
= ∫ ((3x + 7)\(\sqrt{3 x+7}\)) – 3\(\sqrt{3 x+7}\) dx
= ∫ (3x + 7) \(\sqrt{3 x+7}\) dx – 3 ∫ (3x + 7)^{\(\frac{1}{2}\)} dx

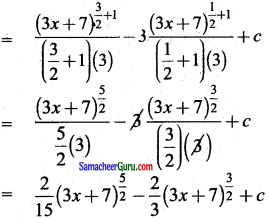
Question 15.
\(\frac{8^{1+x}+4^{1-x}}{2^{x}}\)
தீர்வு :
I = ∫ \(\frac{8^{1+x}+4^{1-x}}{2^{x}}\) dx

= ∫ \(\frac{\left(2^{3}\right)^{1+x}+\left(2^{2}\right)^{1-x}}{2^{x}}\) dx

= ∫ \(\frac{2^{3+3 x}+2^{2-2 x}}{2^{x}}\) dx

= ∫ \(\frac{2^{3+3 x}}{2^{x}}\) dx + ∫ \(\frac{2^{2-2 x}}{2^{x}}\) dx

= ∫ 2^{3 + 3x – x} dx + ∫ 2^{2 – 2x – x} dx

= ∫ 2^{3 + 2x} dx + ∫ 2^{2 – 3x} dx

= \(\frac{2^{3+2 x}}{\log 2}-\frac{2^{2-3 x}}{-3 \log 2}\) + c

= \(\frac{2^{3+2 x}}{\log 2}-\frac{2^{2-3 x}}{3 \log 2}\) + c

Question 16.
I = \(\frac{1}{\sqrt{x+3}-\sqrt{x-4}}\)
தீர்வு :
I = \(\frac{1}{\sqrt{x+3}-\sqrt{x-4}}\)
பகுதியை விகிதப்படுத்த விகிதப்படுத்தும் காரணி

(\(\sqrt{x+3}+\sqrt{x-4}\) ) ஆல் பெருக்கி வகுக்க

I = ∫ \(\frac{\sqrt{x+3}+\sqrt{x-4}}{(\sqrt{x+3}-\sqrt{x-4})(\sqrt{x+3}+\sqrt{x-4})}\) dx

Question 17.
\(\frac{x+1}{(x+2)(x+3)}\)
தீர்வு :
I = ∫ \(\frac{x+1}{(x+2)(x+3)}\) dx

\(\frac{x+1}{(x+2)(x+3)}=\frac{A}{x+2}+\frac{B}{x+3}\) (பகுதி பின்ன

⇒ x + 1 =A(x + 3) + B(x + 2) …………(1)
(1) -ல் x =-3 என பிரதியிட
– 3 + 1 = B(-3 + 2)
⇒ -2 = B(-1) ⇒ B = 2
(1)-ல் x = -2 என பிரதியிட
– 2 + 1 = A(-2 + 3) – 1 ⇒ A(1) = A ⇒ A = -1
∴ \(\frac{x+1}{(x+2)(x+3)}\) = \(\frac{-1}{x+2}+\frac{2}{x+3}\) dx

∴ I = ∫ \(\frac{(x+1)}{(x+2)(x+3)}\) dx

= ∫ \(\frac{-1}{x+2}\) dx + ∫ \(\frac{2}{x+3}\) dx
= – log |x + 2| + 2log |x + 3| + c = 2 log |x + 3| -log |x + 2| + c

Question 18.
\(\frac{1}{(x-1)(x+2)^{2}}\)
தீர்வு :
I = ∫ \(\frac{1}{(x-1)(x+2)^{2}}\) dx என்க
\(\frac{1}{(x-1)(x+2)^{2}}\) = \(\frac{\mathrm{A}}{x-1}+\frac{\mathrm{B}}{x+2}+\frac{\mathrm{C}}{(x+2)^{2}}\)
[பகுதி பின்னமாக்கியதால்]

⇒ I = A (x + 2)² + B (x – 1) (x + 2) + C (x – 1) …. (1)
∴ x = -2 என (1)-ல் பிரதியிட
1 = C(- 2 – 1)
⇒ 1 = C (-3)
⇒ C = \(-\frac{1}{3}\)
3 (1)-ல் x = 1 என்க.
1 = (A) (1 + 2)²
⇒ 1 = A(9) ⇒ A = \(\frac{1}{9}\)
(1)-ல் x = 0 என்க
1 = 4A+ B (-2) + C(-1)
⇒ 1 = 4A – 2B – C
⇒ 1 = 4(\(\frac{1}{9}\)) -2B – (-\(\frac{1}{3}\))

⇒ 1 = \(\frac{4}{9}\) – 2B + \(\frac{1}{3}\)

⇒ 2B = \(\frac{4}{9}\) + \(\frac{1}{3}\) – 1 = \(\frac{4+3-9}{9}=\frac{-2}{9}\)

⇒ B = \(-\frac{1}{9}\)

Question 19.
\(\frac{3 x-9}{(x-1)(x+2)\left(x^{2}+1\right)}\)
தீர்வு :
I = ∫ \(\frac{3 x-9}{(x-1)(x+2)\left(x^{2}+1\right)}\) dx

\(\frac{(3 x-9)}{(x-1)(x+2)\left(x^{2}+1\right)}\) = \(\frac{\mathrm{A}}{x-1}+\frac{\mathrm{B}}{x+2}+\frac{\mathrm{C} x+\mathrm{D}}{x^{2}+1}\)
(பகுதி பின்னமாக்கியதால்)
⇒ 3x – 9 = A (x + 2) (x² + 1) +B(x – 1) (x² + 1) (Cx +D)(x – 1) (x + 2) … (1)
x = 1 என (1)ல் பிரதியிட
-6 = A (3) (2)
⇒ -6 = A(6)
⇒ A = -1
x = – 2 என (1)- ல் பிரதியிட
-15 = B(-3)(5)
⇒ -15 = -15
⇒ B = \(\frac{15}{15}\) = 1
x = 0 என (1) ல் பிரதியிட
-9 = 2A – B – 2D
-9 = -2 -1 -2D
⇒ -9 = -3 -2D
⇒ -9 + 3 = -2D
⇒ – 6 =-2D ⇒ D = 3 x = -1 என (1) ல் பிரதியிட
-12 = A(1) (2) + B (-2) (2) + (-C + D) (-2) (1)
⇒ -12 = 2A – 4B + 2C – 2D
⇒ -12 = -2 – 4 + 2C – 6
⇒ -12 = -12 + 2C
⇒ C = 0
∴ \(\frac{3 x-9}{(x-1)(x+2)\left(x^{2}+1\right)}\) = \(\frac{-1}{x-1}+\frac{1}{x+2}+\frac{3}{x^{2}+1}\)

∴ I = ∫ \(\frac{(3 x-9) d x}{(x-1)(x+2)\left(x^{2}+1\right)}\) dx

= \(-1 \int \frac{d x}{x-1}+\int \frac{d x}{x+2}+3 \int \frac{d x}{x^{2}+1}\)

= -log|x – 1| + log|x + 2| + 3 tan^-1 x + c

= log \(\left|\frac{x+2}{x-1}\right|\) + 3 tan^-1 x + c

Question 20.
\(\frac{x^{3}}{(x-1)(x-2)}\)
தீர்வு :
I = ∫ \(\frac{x^{3}}{(x-1)(x-2)}\) dx

= ∫ \(\frac{x^{3}}{x^{2}-3 x+2}\) dx