Samacheer Kalvi 11th Maths Guide Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 11 கணங்கள், தொடர்புகள் மற்றும் naசார்புகள் Ex 11.8 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 11 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 11.8

கீழ்க்காண்பவற்றைத் தொகையிடுக…

Question 1.
(i) e^x cos bx
(ii) e^2x sin x
(iii) e^-x cos 2x
என்க :
u = cos bx என்க dv= e^ax dx
du = -b sin bx dx; v = \(\frac{e^{a x}}{a}\)
பகுதி தொகையிடலைப் பயன்படுத்த
I = ∫ uv – ∫ vdu
= \(\frac{e^{a x}}{a}\) cosbx + ∫ \(\frac{e^{a x}}{a}\) sin bx dx

= \(\frac{e^{a x}}{a}\) cos bx + ∫ \(\frac{b}{a}\) e^ax sin bx dx

I = \(\frac{e^{a x}}{a}\) cos bx + \(\frac{b}{a}\) I₁ …………(1)

I₁ = ∫ e^ax sin bx dx
u = sin bx; dv = e^ax dx

du = b cos bx dx; v = \(\frac{e^{a x}}{a}\)

பகுதி தொகையிடலைப் பயன்படுத்த

I₁ = uv – ∫ v du

= \(\frac{e^{a x} \sin b x}{a}\) – ∫ \(\frac{e^{a x}}{a}\) . b . cos bx dx

= \(\frac{e^{a x} \sin b x}{a}\) – \(\frac{b}{a}\) ∫ e^ax cos bx . dx

I₁ = \(\frac{e^{a x} \sin b x}{a}\) – \(\frac{b}{a}\) I

(1) -ல் I₁ -பிர்திபபிட

I = \(\frac{e^{a x} \sin b x}{a}\) cos bx + \(\frac{b}{a}\) (\(\frac{e^{a x} \sin b x}{a}\) sin bx – \(\frac{b}{a}\) I)

= \(\frac{e^{a x} \sin b x}{a}\) cos bx + \(\frac{b}{a^{2}}\) e^ax sin bx – \(\frac{b^{2}}{a^{2}}\) I

⇒ (1 + \(\frac{b^{2}}{a^{2}}\)) I = \(\frac{a e^{a x} \cos b x+b e^{a x} \sin b x}{a^{2}}\)

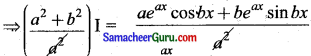
I = \(\frac{e^{a x}}{a^{2}+b^{2}}\) [a cos bx + b sin bx] + c

(ii) e^2x sin x

I = ∫ e^2x sin x dx

∫ e^ax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx)
a = 2, b = 1
∴ I = ∫ e^2x sin x dx

= \(\frac{e^{2 x}}{2^{2}+1^{2}}\) (2 sin x – cos x) + concosbx

= \(\frac{e^{2 x}}{5}\) (2 sin x – cos x) + c

(iii) e^-x cos 2x

I = ∫ e^-x cos 2x dx

= ∫ e^ax cos bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) [a cos bx + b sin bx] + c

இங்கு a = -1, b = 2

∴ I = ∫ e^-x cos 2x dx

= \(\frac{e^{-x}}{(-1)^{2}+2^{2}}\) [-cos 2x + 2 sin 2x] + c

= \(\frac{e^{-x}}{5}\) [2 sin 2x – cos 2x] + c

Question 2.
(i) e^-3x sin 2x
(ii) e^-4x sin 2x
(iii) e^-3x cos x
என்க :
(i) I = ∫ e^-3x sin 2x dx

∫ e^ax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx) + c

இங்கு a = -3, b = 2

∴ I = ∫ e^-3x sin 2x dx

= \(\frac{e^{-3 x}}{(-3)^{2}+2^{2}}\) [-3 sin 2x – 2 cos 2x] + c

= \(\frac{e^{-3 x}}{13}\) [3 sin 2x + 2 cos 2x] + c

(ii) e^-4x sin 2x

I = ∫ e^-4x sin 2x dx

∫ e^ax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx) + c

இங்கு a = -4, b = 2

I = ∫ e^-4x sin 2x dx

= \(\frac{e^{-4 x}}{(-4)^{2}+2^{2}}\) [-4 sin 2x – 2 cos 2x] + c

= \(\frac{e^{-4 x}}{20}\) [4 sin 2x + 2 cos 2x] + c

= \(\frac{e^{-4 x}}{10}\) [2 sin 2x + 2 cos 2x] + c

(iii) e^-3x cos x

I = ∫ e^-3x cos x dx

∫ e^ax sin bx dx = \(\frac{e^{a x}}{a^{2}+b^{2}}\) (a sin bx – b cos bx) + c

இங்கு a = -3, b = 1

∴ I = ∫ e^-3x cos x dx

= \(\frac{e^{-3 x}}{(-3)^{2}+1^{2}}\) [-3 cos x + sin x] + c

= \(\frac{e^{-3 x}}{10}\) [sin x – 3 cos x] + c