Samacheer Kalvi 11th Maths Guide Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.12

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.12 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.12

கேள்வி 1.
b > 0 மற்றும் b ≠ 1. எனில், y = b^x-ஐ மடக்கை அமைப்பில் எழுதுக. மேலும், இந்த மடக்கைச் சார்பின் சார்பகம் மற்றும் வீச்சகம் ஆகியவற்றை எழுதுக.
தீர்வு:
y = b^x
மடக்கை வடிவில் எழுத log, y = x இந்த மடக்கைச் சார்பின் சார்பகம் மிகை மெய்யெண்களின் கணமாகும் மற்றும் வீச்சகம் மெய்யெண்கள்
கணமாகும். log_by = x, (0, ∞), (-∞, ∞)

கேள்வி 2.
மதிப்பு காண்க : log₉27 – log₂₇9
தீர்வு:
log₉27 – log₂₇9 ⇒ log₉3³ – log₂₇3²

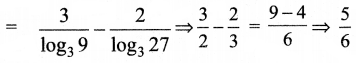
கேள்வி 3.
log₈x + log₄x log₂x = 11-ன் தீர்வு காண்க.
தீர்வு:
கொடுக்கப்பட்டது: log₈x + log₄x log₂x = 11

கேள்வி 4.
log₄2^8x = 2^log₂8 -ன் தீர்வு காண்க
தீர்வு:

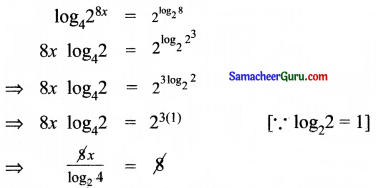
⇒ x = log₂4
⇒ x = log₂2²
⇒ x = 2log₂2
⇒ x = 1

கேள்வி 5.
a² + b² = 7ab எனில், log\(\left(\frac{a+b}{3}\right)\) = \(\frac{1}{2}\)(log a + log b) எனக் காண்க.
தீர்வு:
கொடுக்கப்பட்டது : a² + b² =7ab 2ab ஐ இருபுறமும் கூட்ட
⇒ a² + b² + 2ab = 7ab + 2ab
⇒ (a + b)² = 9ab
⇒ \(\frac{(a+b)^{2}}{9}=(a b)^{\frac{1}{2}}\)
⇒ \(\left(\frac{a+b}{3}\right)^{2}\) = ab
இருபுறமும் வர்க்கமூலம் காண
⇒ \(\frac{a+b}{3}\) = √ab
⇒ log\(\left(\frac{a+b}{3}\right)\) = log\((a b)^{\frac{1}{2}}\)
= \(\frac{1}{2}\) log(ab)
log\(\left(\frac{a+b}{3}\right)\) = \(\frac{1}{2}\)[log a + log b]
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
\(\log \frac{a^{2}}{b c}+\log \frac{b^{2}}{c a}+\log \frac{c^{2}}{a b}\) = 0 என நிறுவுக.
தீர்வு:

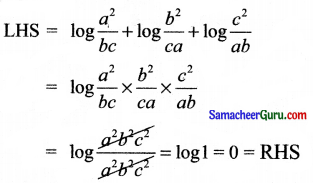
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 7.
log 2 + 16 log \(\frac{16}{15}\) + 12 log \(\frac{25}{24}\) + 7 log \(\frac{81}{80}\) = 1 என நிறுவுக.
தீர்வு:

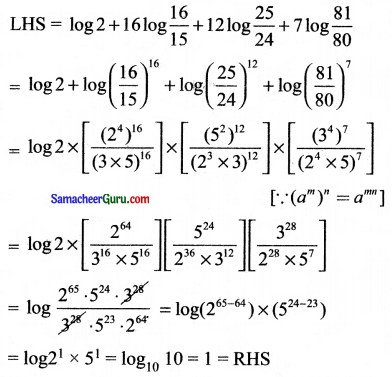
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 8.
log_a²a log_b²b log_c²c = \(\frac{1}{8}\) என நிறுவுக.
தீர்வு:

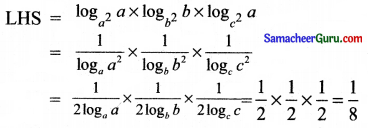
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 9.
log a + log a² + log a³ + ….. + log aⁿ = \(\frac{n(n+1)}{2}\) log a என நிறுவுக.
தர்வு:
LHS = log a + log a² + log a³ + ….. + log aⁿ
= log a + 2 log a + 3 log a+ ….. + n log a
= log a (1 + 2 + 3 + ……. n)

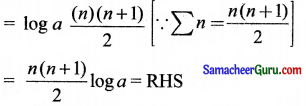
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 10.
\(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\) எனில், xyz = 1 எனக் காண்க.
தீர்வு:
\(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\)
⇒ log x = k (y – z) = ky- kz … (1)
log y = k (z – x) = kz – ka ….(2)
log z = k (x – y) = kx – ky ….(3)
(1), (2) மற்றும் (3) ஐக் கூட்டுக.

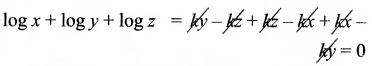
⇒ log xyz = 0 = log 1
∴ xyz = 1
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 11.
log₂x – 3log_{\(\frac{1}{2}\)} x = 6-ன் தீர்வு காண்க.
தீர்வு:

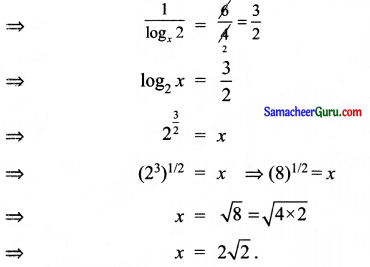
கேள்வி 12.
log_5-x (x² – 6x + 65) = 2-ன் தீர்வு காண்க.
தீர்வு:
கொடுக்கப்பட்டது: log_5-x (x² – 6x + 65) = 2
⇒ x² – 6x + 65 = (5 – x)²
⇒ x² – 6x + 65 = 25 + x² – 10x
⇒ 10x – 6x = -65 + 25
⇒ 10x – 6x = -65 +25
⇒ 4x = -40.
∴ x = -10.