Samacheer Kalvi 11th Maths Guide Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 அடிப்படை இயற்கணிதம் Ex 2.3

கேள்வி 1.
கீழ்க்கண்ட அசமன்பாடுகளை இடைவெளி அமைப்பில் எழுதுக.
(i) x ≥ -1 மற்றும் x < 4
(ii) x < 5 மற்றும் x ≥ -3
(iii) x < -1 அல்லது x < 3
(iv) – 2x > 0 அல்ல து 3x – 4 < 11
தீர்வு:
(i) x ≥ -1 மற்றும் x < 4

⇒ x ∈ [-1, 4)

(ii) x ≤ 5 மற்றும் x ≥ -3

⇒ x ∈ [-3, 5]

(iii) x < -1 அல்லது x < 3

⇒ x ∈ [-∞, 3]

(iv) – 2x > 0 அல்ல து 3x – 4 < 11
⇒-2x > 0 அல்லது 3x – 4 < 11
⇒ – x > 0 அல்லது 3x < 11 + 4
⇒ x < 0 அல்லது 3x < 15

⇒ x < 0 அல்லது x < \(\frac{15}{3}\)
⇒ x ∈ (-∞, 5] ⇒ x < 0 அல்லது x < 5

கேள்வி 2.
23x < 100-ன் தீர்வை
(i) x ∈ N
(ii) x ∈ Z-க்கு காண்க.
தீர்வு:
23x< 100
(i) x ∈ N எனில்
⇒ 23x < 100 ⇒ x < \(\frac{100}{23}\)
⇒ x < 4.347 ⇒ x = 1, 2, 3, 4
தீர்வுகணம் {1, 2, 3,4}

(ii) x ∈ Z எனில்
x < 4.347
⇒ x = {……-4, -3, -2, -1, 0, 1, 2, 3}

கேள்வி 3.
– 2x ≥ உன் தீர்வை
(i) x ∈ R
(ii) x ∈ Z
(iii) x ∈ N-க்கு காண்க.
தர்வு:
-2x ≥ 9
⇒ -x ≥ \(\frac{9}{2}\)
⇒ x ≤ \(\frac{9}{2}\)
(i) x ∈ R எனில் x ∈ \(\left(-\infty, \frac{-9}{2}\right)\)
(ii) X ∈ Z எனில் x = {- ∞, …… -5}
(iii) x ∈ N எனில், \(\frac{-9}{2}\) ஐ விட சிறிய இயல் எண் எதுவும் இல்லை
∴ x = {}

கேள்வி 4.
தீர்வு காண்க:
(i) \(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
(ii) \(\frac{5-x}{3}<\frac{x}{2}\) – 4
தீர்வ:
(i) \(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
⇒ \(\frac{3 x-6}{5} \leq \frac{10-5 x}{3}\)
⇒ 3(3x – 6) ≤ 5(10 – 5x)
⇒ 9x – 18 ≤ 50 – 25x
⇒ 9x + 25x ≤ 50 + 18
⇒ 34 x ≤ 68
⇒ x ≤ 2
∴ தீர்வு கணம் (-∞, 2]

(ii) \(\frac{5-x}{3}<\frac{x}{2}\) – 4
முழுவதையும் 3 ஆல் பெருக்க,
5 – x < \(\frac{3 x}{2}\) – 12 2 ஆல் பெருக்க
⇒ 10 – 2x < 3x – 24
⇒ 10 + 24 < 3x + 2x
⇒ 34 < 5x ⇒ \(\frac{34}{5}\) < x ⇒ x ≥ \(\frac{34}{5}\)
∴ தீர்வுகணம் \(\left[\frac{34}{5}, \infty\right)\)

கேள்வி 5.
ஒவ்வொன்றும் 100 மதிப்பெண்கள் கொண்ட 5 பாடங்களில் மதிப்பெண்களின் சராசரி 90 அல்லது அதற்கும் மேல் இருந்தால் தரம் A ஆகும். ஒரு நபர் முதல் 4 பாடங்களில் பெற்ற மதிப்பெண்கள் 84, 87, 95, 91 எனில், ஐந்தாம் பாடத்தில் குறைந்தபட்சம் என்ன மதிப்பெண் பெற்றால் தரம் A கிடைக்கும்?
தீர்வு:
ஒருவன் 5வது தேர்வில் எடுத்த மதிப்பெண்கள் x , என்க.
\(\frac{84+87+95+91+x}{5}\) ≥ 90 ⇒ \(\frac{357+x}{5}\) ≥ 90
இருபுறமும் 5ஆல் பெருக்க               ⇒ 357 + x ≥ 450
இருபுறமும் 357 ஐ கழிக்க
x ≥ 450 – 357 ⇒ x ≥ 93
∴ அவர் A கிரேடு வாங்க 93 மதிப்பெண்களை குறைந்தபட்சமாக பெற்றிருக்க வேண்டும்.

கேள்வி 6.
ஒரு உற்பத்தியாளர் 12 விழுக்காடு அமிலம் கொண்ட 600 லிட்டர் கரைசல் வைத்திருக்கிறார். இதனுடன் எத்தனை லிட்டர்கள் 30 விழுக்காடு அமிலத்தைக் கலந்தால் 15 விழுக்காட்டிற்கும் 18 விழுக்காட்டிற்கும் இடைப்பட்ட அடர்த்தி கொண்ட அமிலக் கரைசல் கிடைக்கும்?
தீர்வு:
30 விழுக்காடு அமிலம் கலந்த கரைசல் = x லிட்டர் என்க .
∴ மொத்த கரைசல் = (600 +x) லிட்டர்
30%x + 12% 600 > 15% (600 + x)
⇒ \(\frac{30 x}{100}+\frac{12}{100}\) × 600 > \(\frac{15}{100}\)(600 + x)
⇒ 30x + 7200 > 9000 + 15 x (100 ஆல் பெருக்க)
⇒ 15x + 7200 > 9000
⇒ 15x > 9000 – 7200
⇒ 15x > 1800
⇒ x > 120 …. (1)
30% of x + 12% of 600 < \(\frac{18}{100}\) (600 + x) ⇒ \(\frac{30 x}{100}+\frac{12}{100}\) × 600 > \(\frac{18}{100}\)(600 + x)
⇒ 30x + 7200 < 18(600 + x)
⇒ 30x +7200 < 10800 + 18 x
⇒ 12x + 7200 < 10800
⇒ 12x < 10800 – 7200
⇒ 12x < 3600

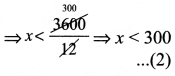
(1), (2) லிருந்து 120 < x < 300
∴ 30% அமிலம் கலந்த கரைசல் 120 லிட்டரைவிட அதிகமாகவும் மற்றும் 300 லிட்டரை விட குறைவாகவும் கிடைக்கும்.

கேள்வி 7.
10ஐ விடப் பெரிய அடுத்தடுத்த இரண்டு ஒற்றைப்படை இயல் எண்களின் கூடுதல் 40ஐ விடக் குறைவாக இருக்க வேண்டுமெனில், அவ்வெண்களைக் காண்க.
தீர்வு:
முதல் ஒற்றைப்படை இயல் எண் = x
என்க அடுத்த ஒற்றைப்படை இயல் எண் = x + 2
⇒ x > 10 கொடுக்கப்பட்ட கூற்று  …(1)
⇒ x + 2 > 1
⇒ x > 8 ….. (2)
x + x + 2 < 40 ….. (3)
(1), (2) லிருந்து ⇒ x > 10  ……. (4)
(3) லிருந்து 2x + 2 < 40
⇒ 2x < 38
⇒ x < \(\frac{38}{2}\) ⇒ x < 19  ……. (5)
(4), மற்றும் (5) லிருந்து 10 < x < 19
x ஒற்றைப்படை இயல் எண்கள் என்பதால் x = 11, 13, 15, 17
∴ தேவையான ஜோடிகள் (11, 13),(13, 15),(15, 17) (17, 19).

கேள்வி 8.
ஒரு ஏவுகணை ஏவப்படுகிறது. t வினாடிகளுக்குப் பிறகு தரையில் இருந்து அதன் உயரம் h ஆனது h(t) = -5t² + 100t , 0 ≤ t ≤ 20 எனக் கொடுக்கப்பட்டுள்ளது. ஏவுகணை எந்நேரங்களில் 495 அடி உயரத்தை அடையும்.
தீர்வு:
ht = -5t² + 100t, 0 ≤ t ≤ 20
ஏவுகணை 495 அடி உயரத்தை அடையும்பொழுது வினாடி என்க
∴ 0 < h(t) < 495
⇒ 0 < -5t² + 100t < 495
⇒ 0 < -5t² + 100t – 495 < 0
⇒ -5t² + 100t – 495 < 0
⇒ t² – 20t + 99 < 0 ⇒ (t – 11) (t – 9) = 0 ⇒ t = 11, 9
∴ 11 அல்லது 9 வினாடி நேரத்தில் 495 அடி உயரத்தை ஏவுகணை அடையும்.

கேள்வி 9.
தண்ணீர் குழாய் சரி செய்பவருக்குப் பின்வரும் முறைகளில் கூலி கொடுக்கப்படுகிறது. முதல் முறையில் ₹ 500-ம் ஒவ்வொரு மணி நேரத்திற்கும் ₹ 70 கணக்கிடப்பட்டுக் கொடுக்கப்படுகிறது, இரண்டாம் முறையில் ஒவ்வொரு மணி நேரத்திற்கு ₹ 120 எனக் கொடுக்கப்படுகிறது. ஒருவர் x மணி நேரம் வேலை செய்கிறார். எனில் x -ன் எம்மதிப்பிற்கு முதல் முறையில் அவருக்கு சிறந்த கூலி கிடைக்கும்?
தீர்வு:
ஒரு வேலையை முடிக்க ஆகும் நேரம் = x
என்க முதல் முறையில் சம்பளம் = 500 + 70x
இரண்டாம் முறையில் சம்பளம் = 120x
500 + 70x > 120x எனத் தரப்பட்டுள்ளது
⇒ 500 > 120x – 70x
⇒ 500 > 50 x

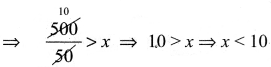
∴ 10 மணிக்கு குறைவாக அவருக்கு சிறந்த கூலி கிடைக்கும்.

கேள்வி 10.
A மற்றும் B ஆகியோர் ஒரே மாதிரியான வேலை தீ செய்தாலும், அவர்களது வருட ஊதியம் ₹6000க்கு மேல் வேறுபாடாக இருக்கிறது. B-ன் மாத ஊதியம் ₹27,000 எனில் A-ன் மாத ஊதியத்திற்கான சாத்தியக் கூறுகளைக் காண்க.
தீர்வு:
A-ன் ஊதியம் = x என்க.
B-ன் ஊதியம் = 6000 + x.
B -ன் மாத ஊதியம் ₹27,000 எனில்
6000 + x < 27000 ⇒ x < 27000 – 6000
⇒ x < 21,000
∴ A-ன் ஊதியம் < ₹21,000 அல்லது ₹ 33,000.