Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.10

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.10 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.10

கேள்வி 1.
∠B = 88°, a = 23, = 2 என்ற அளவுகளைக் கொண்ட முக்கோணங்கள் ஒன்றா அல்லது இரண்டா? அல்லது முக்கோணம் வரைய இயலாதா? ! முக்கோணம் உண்டு எனில், அதன் தீர்வைக் காண்க.
தீர்வு:

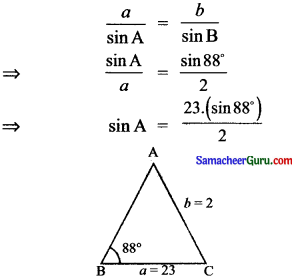
⇒ sin A = 23 × 0.999
sin A = 22.99 இது பொருந்தாது
∴ முக்கோணத்திற்கு தீர்வு இல்லை.

கேள்வி 2.
∆ ABC இல் a = 4, b = 6 மற்றும் C = 8 எனில் 4 cos B + 3 cos C = 2 எனக் காண்பி.
தீர்வு:
L.H.S = 4 cos B + 3 cos C.


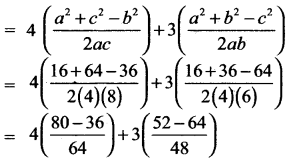
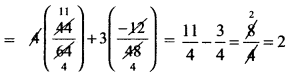
= RHS எனவே நிரூபிக்கப்பட்டது.

கேள்வி 3.
∆ ABC இல் a = √3 – 1, b = √3 + 1 மற்றும் C = 60° எனில், மூன்றாவது பக்கம் மற்றும் இரு கோணங்களைக் காண்க.
தீர்வு:
நேப்பியரின் சூத்திரத்தின் படி

கேள்வி 4.
∆ABC இல் முக்கோணத்தின் பரப்பளவு ∆ = \(\frac{b^{2}+c^{2}-a^{2}}{4 \cot A}\) என நிறுவுக.
தீர்வு:

கேள்வி 5.
∆ABC இல் a = 12 செ.மீ. b = 8 செ.மீ மற்றும் c = 30° எனில் முக்கோணத்தின் பரப்பு 24 ச.செ.மீ. எனக் காண்பி.
தீர்வு:
∆ ABC -ன் பரப்பு = \(\frac{3}{2}\) ab sin c
= \(\frac{1}{2}\) × 12 × 8 sin 30°

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
∆ABC இல் a = 18 செ.மீ. b = 24 செ.மீ மற்றும் c = 30 செ.மீ. எனில் ∆ABC இன் பரப்பு 216 ச.செ.மீ எனக் காண்பி.
தீர்வு:
a = 8, b = 24, c = 30
ஹிரான்ஸ் சூத்திரத்தைப் பயன்படுத்தி

கேள்வி 7.
பூமிக்கு அடியில் ஒரே நேர்க்கோட்டில் அமைந்துள்ள இரண்டு வெவ்வேறு குழிகளில் A மற்றும் B என்ற இராணுவ வீரர்கள் பதுங்கி, மலை உச்சியில் ஒரு ஊடுருபவரை கவனித்தனர். A மற்றும் B லிருந்து ! ஊடுருபவரின் கோணங்கள் கிழக்கு திசையில் முறையே 30° மற்றும் 45° மற்றும் Aக்கு நக்கு இடைப்பட்ட தொலைவு 5 கி.மீ. எனில் B-யிலிருந்து ஊடுருபவரின் தொலைவினைக் காண்க.
தீர்வு:
P என்பவர் ஊடுருபவர், மற்றும் A, B என்பவர்கள் இராணுவ வீரர்கள் என்க.
X என்பது Pக்கும் B க்கும் இடைப்பட்ட தூரம்
∆ABP -யில்
∠PAB = 30°, ∠PBC = 45°
∠APB = 15°

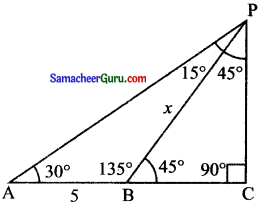
∆ABP-ல் சைன் விதிப்படி
⇒ \(\frac{5}{\sin 15^{\circ}}=\frac{x}{\sin 30^{\circ}}\)
⇒ x = \(\frac{5}{\sin 15^{\circ}}\) × sin30° = 5 × \(\frac{1}{2 \sin 15^{\circ}}\) …(1)
= sin 15° = sin (45 – 30)
= sin45° cos 30° – cos 45° sin 30°
= \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}} \times \frac{1}{2}=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
(1) ல் sin 15°ன் மதிப்பை பிரதியிட

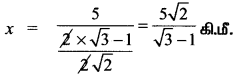
கேள்வி 8.
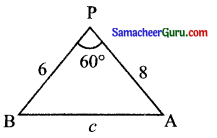
ஓர் ஆராய்ச்சியாளர் ஓர் குளத்தின் அகலத்தைக் கிழக்கிலிருந்து மேற்காகச் சரியாக அளவிட முடியாதபோது அதைக் கண்டறிய விழைகிறார். P என்ற புள்ளியிலிருந்து குளத்தின் கிழக்குப் பகுதியின் முனை 8 கி.மீ. தொலைவிலும் அதே சமயத்தில் மேற்கு பகுதியின் முனை 6 கி.மீ. தொலைவிலும் உள்ளது மற்றும் P-யையும் கிழக்குப் பகுதியின் முனையை இணைக்கும் கோட்டிற்கும், Pயையும் மேற்கு பகுதியின் முனையையும் இணைக்கும் கோட்டிற்கும் இடைப்பட்டக் கோணம் 60° எனில் குளத்தின் அகலத்தைக் காண்க.
தீர்வு:
கிழக்குப்பகுதியில் உள்ள புள்ளி A, மேற்குப்பகுயில் உள்ள புள்ளி B என்க.
PA = 8, PB = 6
a = 6, b = 8, ∠C = 60
கொசைன் விதிப்படி
c² = a² + b² – 2ab cos C
= 36 + 64 – 2(6) (8) cos 60°


c = √52 = \(\sqrt{4 \times 13}\) = 2√13
∴ c = 2 13 கி.மீ.
∴ குளத்தின் அகலம் = 2 13 கி.மீ.

கேள்வி 9.
கடல் மட்டத்திலிருந்து ஒரே உயரத்தில் வங்காள விரிகுடாவிற்கு மேல் A மற்றும் B என்ற இரண்டு கடற்படை ஹெலிகாப்டர்கள் தொலைந்த படகைத் தேடுகின்றன. 10 கி.மீ. இடைவெளியில் அவைகள் பறக்கும்போது அதன் பைலட்டுகள் ஒரே நேரத்தில் அந்தப் படகைப் பார்க்கிறார்கள். A இலிருந்து படகு 6 கி.மீ. தூரத்தில் உள்ளது. மேலும், கோட்டுத்துண்டு AB படகில் தாங்கும் கோணம் 60° எனில், Bஇற்கும் படகிற்கும் உள்ள தொலைவைக் காண்க.
தீர்வு:
A, B பைலட்களின் இருப்பிடம். C படகின் இருப்பிடம்
கொசைன் விதிப்படி c² = a² + b² – 2ab cos C

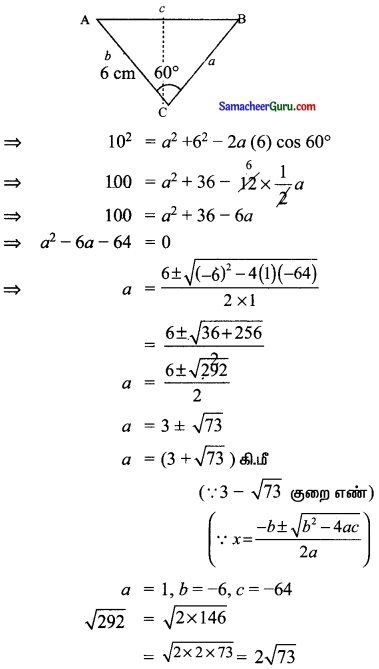
கேள்வி 10.
ஒரு மலை வழியாக ஒரு நேர்க் குகை அமைக்கையில், மலைக்கு எதிரே உள்ள P என்ற புள்ளியிலிருந்து மலையின் இரு முனைகள் A மற்றும் B னை நிலமளப்பவர் காண்கிறார். AP= 3 கி.மீ , BP= 5 கி.மீ , ∠APB =120° எனில் மலைக்குகையின் நீளத்தினைக் காண்க.
தீர்வு:
AB = c என்பது மலைக்குகையின் நீளம் என்க.
a = 5, b = 3, ∠c = 120°
கொசைன் விதிப்படி

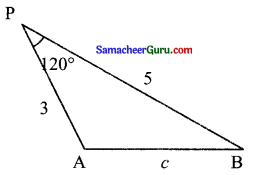
c² = a² + b² – 2ab cos C
= 25 + 9 – 2 (5) cos 120°
= 34 – 30 cos (180 – 60°)
= 34 – 30 (-cos 60°)

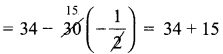
c² = 49,
c = ±7 கி.மீ.
c = -7-ஆக இருக்க முடியாது
c = 7 கி.மீ.
∴ மலைக்குகையின் நீளம் = 7 கி.மீ.

கேள்வி 11.
120 அடி மற்றும் 60 அடி, பக்கங்களின் நீளங்கள் அவற்றிற்கிடைப்பட்ட கோணம் 60° உடைய ஒரு முக்கோண வடிவ நிலத்தை ஒரு முக்கோண வடிவ நிலத்தை ஒரு விவசாயி வாங்க விரும்புகிறார். ஒரு சதுர அடி நிலத்தின் விலை ₹500 எனில், அந்த நிலத்தை வாங்கத் தேவையான மொத்தத் தொகை எவ்வளவு? மேலும் நிலத்தின் சுற்றளவைக் காண்க.
தீர்வு:
b = 60 அடி, c = 120 அடி, ∠A = 60°
கொசைன் விதிப்படி

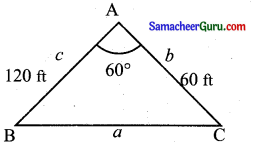
a² = b² + c² – 2bc cos A
= 120² + 60² – 2 × 120 × 60 × cos 60°
= 14400 + 3600 – 7200
a² = 10,800
a = \(\sqrt{100 \times 4 \times 9 \times 3}\)
a = \(\sqrt{400 \times 27}\) = 20√27
∆ கன் சுற்றளவு = 120 + 60 + 20√27
= 180 + 20√27 அடி
முக்கோண வயலின் பரப்பு (∆ ABC) = \(\frac{1}{2}\)bc sin A

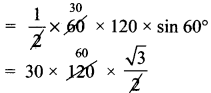
= 30 × 60 × √3
= 1800√3
= 3117.6
1 ச.அடி நிலத்தின் விலை = ₹ 500 எனில்
3117.6 ச.அடி நிலத்தின் விலை = 500 × 3117.6
= ₹ 1,55,800.

கேள்வி 12.
ஒரு போர் ஜெட் விமானம் கிடைமட்டமாகப் பறந்து பூமியிலுள்ள ஒரு சிறு இலக்கைத் தாக்க வேண்டும். அவ்விலக்கை விமானி 30° இறக்கக் கோணத்தில் பார்க்கிறார். 100 கி.மீ. பறந்த பின்பு மீண்டும் அதே இலக்கை 60° இறக்க கோணத்தில் பார்க்கும் அந்த நேரத்தில் ஜெட் விமானத்திற்கும் இலக்கிற்கும் உள்ள! தொலைவு எவ்வளவு?
தீர்வு:
C என்பது இலக்கின் புள்ளி. A, B என்பன விமானியின் இருப்பிடம் என்க.

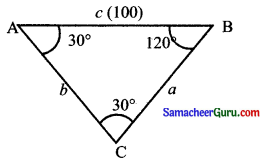
∠BAC = 30°, ∠ABC = 120°
∴ ∠C = 180 – (30 + 120)
= 180° – 150 = 30°
AB = 100 கி.மீ.

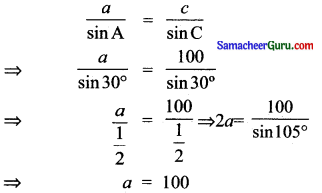
கேள்வி 13.
ஒரு விமானம் ஒரு மைல் கல்லிலிருந்து 1 கி.மீ. தூரத்தில் பறக்கிறது. அதே நேரத்தில் மற்றொரு மைல் கல்லுடன் உள்ள தூரம் 2 கி.மீ. இரண்டு மைல் கல்களும் விமானத்துடன் தாங்கும் கோணம் 45° எனில் இரண்டு மைல் கல்களுக்கு இடைப்பட்ட தூரம் என்ன?
தீர்வு:
A, B என்பன தரையில் உள்ள இரு இடங்கள் C என்பது விமானத்தின் இருப்பிடம் என்க.

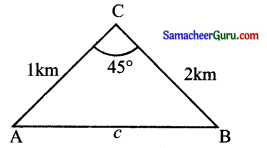
கொசைன் விதிப்படி
c² = a² + b² – 2ab cos C
c² = 2² + 1² – 2(2) (1) cos 45°

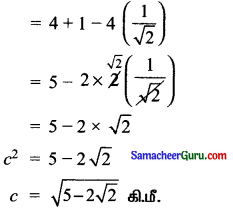
கேள்வி 14.
ஒருவன் காலை நடைப்பயிற்சியின் போது A என்ற புள்ளியில் தொடங்கி B மற்றும் C ஆகிய புள்ளிகளுக்குச் சென்று இறுதியில் மீண்டும் Aவை வந்தடைகிறார். முக்கோணம் ABC இல் ∠A = 60° மற்றும் ∠B = 45°, AC = 4 கி.மீ. எனில், அவர் நடந்த மொத்தத் தொலைவைக் காண்க.
தீர்வு:
AC = 4 கி.மீ. ∠A = 60°
∠B = 45°, ∠C = 180° – (A + B)
= 180 – 105 = 75°
சைன் விதியைப் பயன்படுத்தி

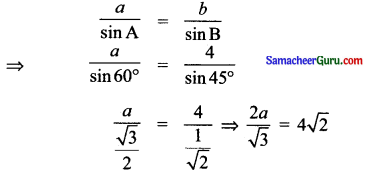
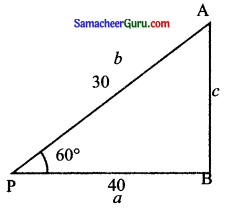
கேள்வி 15.
இரண்டு வாகனங்கள் ஒரு புள்ளி Pலிருந்து ஒரே நேரத்தில் தொடங்கி இரு வெவ்வேறு சாலைகளில் பயணிக்கிறது. ஒரு வாகனம் 60 கி.மீ/மணி, ! மற்றொரு வாகனம் 80 கி.மீ/மணி என்ற சராசரி வேகத்தில் பயணிக்கிறது. அரை மணி நேரத்திற்குப் பிறகு அவ்வாகனங்கள் A மற்றும் Bஐ அடைகின்றன. கோடு AB ஆனது Pஇல் தாங்கும் கோணம் 60° எனில், ABஐக் காண்க.
தீர்வு:
வேகம் 1 = 60 கி.மீ./மணி
நேரம்’ = \(\frac{1}{2}\) மணி
∴ தூரம் = வேகம் × நேரம்


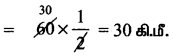
= 80 கி.மீ./மணி
நேரம் = \(\frac{1}{2}\) மணி
∴ தூரம் = வேகம் , நேரம்
= 80 × \(\frac{1}{2}\) = 40 கி.மீ.
∠APB = 60°
கொசைன் விதியைப் பயன்படுத்தி
c² = a² + b² – 2ab cos c
c² = 40² + 30² – 2(40)cos 60°

= 2500 – (40)(30) = 1300
c = √1300 = \(\sqrt{13 \times 100}\)
= 10√13 கி.மீ.

கேள்வி 16.
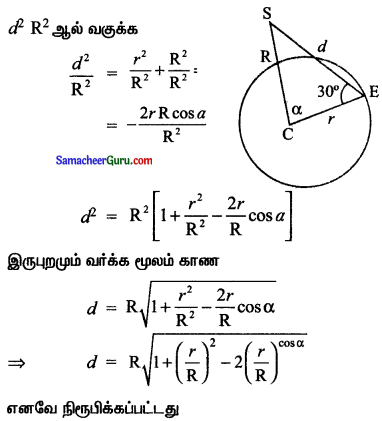
ஒரு செயற்கைக்கோள் ஒரு விண்வெளியில் உள்ளதாகக் கொள்வோம். பூமியிலுள்ள நிலையம் மற்றும் பூமியின் மையம் ஆகியவை ஒரே தளத்தில் அமைகின்றன. பூமியின் அதன் ஆரம் என்றும் அதன் மையத்திலிருந்து செயற்கைக்கோள் R தொலைவில் உள்ளது என்று கொள்வோம். செயற்கைக்கோளுக்கும் செயற்கை கோளின் நிலையத்திற்கும் உள்ள தொலைவு d என்க. செயற்கைக்கோள் நிலையத்திலிருந்து செயற்கைக்கோள் 30° ஏற்றக் கோணத்தில் உள்ளது. செயற்கைக்கோள் மற்றும் பூமியிலுள்ள நிலையம் ஆகியவற்றை இணைக்கும் கோட்டுத்துண்டு பூமியின் மையத்தில் தாங்கும் கோணம் a எனில், d = R \(\sqrt{1+\left(\frac{r}{R}\right)^{2}-2 \frac{r}{R} \cos \alpha}\) என நிறுவுக.
தீர்வு:
S செயற்கைக்கோள், E பூமி, C பூமியின் மையம் என்க.
CE = r, CS = R மற்றும் SE = d, ∠ SCE = α
கொசைன் விதியைப் பயன்படுத்தி
d² = r² + R² – 2r R cos α