Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.11 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.11
கேள்வி 1.
(i) sin-1\(\frac{1}{\sqrt{2}}\)
(ii) cos-1\(\frac{\sqrt{3}}{2}\)
(iii) cosec-1 (-1)
(iv) sec-1 (-√2)
(v) tan-1 (√3)
ஆகியவற்றின் முதன்மை பதிப்பைக் காண்க.
தீர்வு:
(i)

(ii)
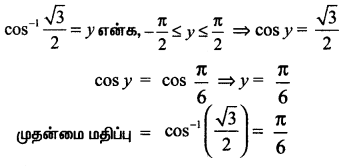
![]()
(iii) cosec-1(-1) = y என்க, \(\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\) = cosecy
[∵ cosec (θ) = -cosec θ]
cosec y = – cosec \(\frac{\pi}{2}\)
cosec y = cosec\(\left(-\frac{\pi}{2}\right)\) ⇒ y = \(\)
முதன்மை மதிப்பு cosec-1(-1) = \(\frac{-\pi}{2}\)
(iv) sec-1 (-√2) = y என்க, (0 ≤ y ≤ π)
sec y = – √2
sec y = – sec \(\frac{-\pi}{4}\)
= sec \(\left(\pi-\frac{\pi}{4}\right)\)
[II கால் பகுதியில் குறையெண்]
y = \(\frac{3 \pi}{4}\)
முதன்மை மதிப்பு sec-1 (-√2) = \(\frac{3 \pi}{4}\)
(v) tan-1 (√3) = y என்க
tan-1 (√3) = \(\left(-\frac{\pi}{2}<y<\frac{\pi}{2}\right)\)
tan y = √3
tan y = tan\(\left(\frac{\pi}{3}\right)\) ∴ y = \(\frac{\pi}{3}\)
முதன்மை மதிப்பு tan-1 (√3) = \(\frac{\pi}{3}\)
![]()
கேள்வி 2.
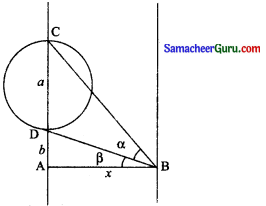
x மீட்டர் அகலமுடைய பாதையின் ஒரு புறத்திலிருந்து பாதையின் மறுபக்கம் அமைக்கப்பட்ட 1 மீட்டர் விட்டமுடைய வட்ட வடிவப் போக்குவரத்து சமிக்கையின் பச்சை விளக்கா ஒருவர் பார்க்கிறார். பச்சை விளக்கின் அடிப் பகுதியிலிருந்து பார்ப்பவரின் கண்ணின் கிடைமட்டக் கோடு வரையில் உள்ள உயரம் 5 மீட்டர் ஆகும். பச்சை விளக்கின் விட்டம் பார்ப்பவரின் கண்களில் தாங்கும் கோணம் α எனில் α = tan-1\(\left(\frac{a+b}{x}\right)\) – tan-1\(\left(\frac{b}{x}\right)\) என நிறுவுக.
தீர்வு:
பச்சை விளக்கின் விட்டம் DC = a என்க
∠CBD = a
DA = b
AB = x
சாலையின் விட்டம் என்க

![]()