Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.2

கேள்வி 1.
பின்வரும் கோணங்களை ஆரையன் அளவுகளில் கூறுக.
(i) 30°
(ii) 135°
(iii) 205°
(iv) 150
(v) 330°
தீர்வு:
(i) 30° = 30 × \(\frac{\pi}{180}=\frac{\pi}{6}\) ஆரையன்கள்
(ii) 135° = 135 × \(\frac{\pi}{180}=\frac{3 \pi}{4}\) ஆரையன்கள்
(iii)-205° = -205 × \(\frac{\pi}{180}=\frac{-41 \pi}{36}\) ஆரையன்கள்
(iv) 150° = 150 × \(\frac{\pi}{180}=\frac{5 \pi}{6}\) ஆரையன்கள்
(v) 330° = 330 × \(\frac{\pi}{180}=\frac{11 \pi}{6}\) ஆரையன்கள்

கேள்வி 2.
பின்வரும் கோணத்தின் ஆரையன் அளவை பாகை அளவுகளில் காண்க.
(i) \(\frac{\pi}{3}\)
(ii) \(\frac{\pi}{9}\)
(iii) \(\frac{2 \pi}{5}\)
(iv) \(\frac{7 \pi}{3}\)
(v) \(\frac{10 \pi}{9}\)
தீர்வு:
(i) \(\frac{\pi}{3}=\frac{\pi}{3} \times \frac{180}{\pi}\) = 60°
(ii) \(\frac{\pi}{9}=\frac{\pi}{9} \times \frac{180}{\pi}\) = 20°
(iii) \(\frac{2 \pi}{5}=\frac{2 \pi}{5} \times \frac{180}{\pi}\) = 72°
(iv) \(\frac{7 \pi}{3}=\frac{7 \pi}{3} \times \frac{180}{\pi}\) = 420°
(v) \(\frac{10 \pi}{9}=\frac{10 \pi}{9} \times \frac{180}{\pi}\) = 200°

கேள்வி 3.
ஒரு தடகள வீரர் 1 கி.மீ-ஐக் கடக்க வட்ட ஓடு பாதையை 5 முறை சுற்றி வரவேண்டும் எனில் வட்ட ஓடு பாதையின் ஆரம் என்ன?
தீர்வு:
தடகள வீரர் கடக்க வேண்டிய தூரம் = 1 கிமீ

1 கி.மீ கடக்க சுற்றிய சுற்றுகள் = 5
5 × 2πr = 1 கிமீ = 1000 மீ
5 × 2 × \(\frac{22}{7}\) × r = 1000 மீ
r = 1000 × \(\frac{1}{10} \times \frac{7}{22}=\frac{700}{22}\)
r = 31.818
ஓடு பாதையின் ஆரம் r = 31.82 மீ.

கேள்வி 4.
ஒரு வட்டத்தின் விட்டம் 40 செ.மீ., ஒரு நாணின் நீளம் 20 செ.மீ. எனில், சிறிய வில்லின் நீளத்தைக் காண்க.
தீர்வு:
வட்டத்தின் விட்டம் = 40 செ.மீ.

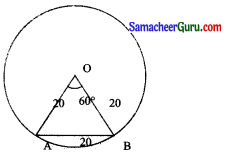
AB = 20
OA = OB = AB = 20 செ.மீ.
∴ ∆ OAB-ல் ∠ AOB = 60°
(∵ ∆ OAB ஒரு சமபக்க முக்கோணம்)
θ = \(\frac{\pi}{3}\)
θ = \(\frac{l}{r}\) ⇒ l = rθ
= 20 × \(\frac{\pi}{3}\) = 20 × \(\frac{22}{7} \times \frac{1}{3}\)
= 20.95செ.மீ.(தோராயமாக).

கேள்வி 5.
100 செ.மீ. ஆரமுடைய வட்டத்தில், 22 செ.மீ. நீளமுடைய வட்டவில் மையத்தில் தாங்கும் கோணத்தைப் பாகையில் காண்க.
தீர்வு:
ஆரம் = 100 செ.மீ.
வில்லின் நீளம் = 22 செ.மீ.
வில். l ஆனது மையத்தில் தாங்கும் கோணம் θ என்க

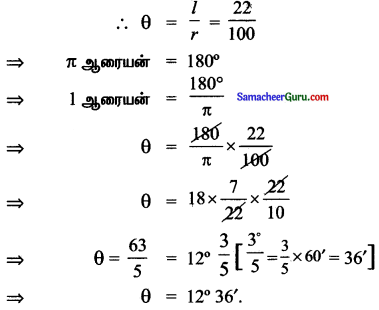
கேள்வி 6.
10 அடி ஆரம் கொண்ட ஒரு வட்டத்தில், θ = 41°-ஐ மையக் கோணமாகக் கொண்ட வட்ட வில்லின் நீளம் காண்க.
தீர்வு:
மையக்கோணம் θ = 41°
ஆரம் r = 10
அடி வில்லின் நீளம் l என்க

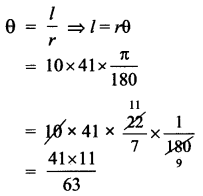
வில்லின் நீளம் 1=7.158 = 7.16 அடி.

கேள்வி 7.
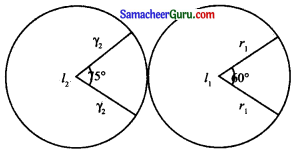
இரண்டு வட்டங்களில், ஒரே அளவு கொண்ட வில்லின் நீளங்கள் 60° மற்றும் 75°-ஐ மையக் ‘கோணங்களாகத் தாங்கும்போது. அவ்விரு வட்டங்களுக்கான ஆரங்களின் விகிதம் காண்க.
தீர்வு:
இரண்டு வட்டங்களில் ஒரே அளவு கொண்ட வில்லின் நீளங்கள் தாங்கும் கோணங்கள் 60°, 75° அவற்றின் ஆரங்கள் r₁, r₂ என்க.
θ = 60° = 60 × \(\frac{\pi}{180}=\frac{\pi}{3}\) ஆரையன்

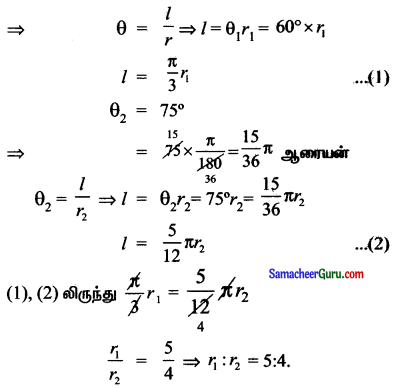
கேள்வி 8.
ஒரு வட்ட கோணப் பகுதியின் சுற்றளவும் அதே ஆரமுடைய அரைவட்டத்தின் வில்லின் நீளமும் சமம் எனில், அவ்வட்டக் கோணப் பகுதியின் மையக் கோணத்தைப் பாகை, கலை மற்றும் விகலையில் காண்க.
தீர்வு:
வட்டத்தின் ஆரம் = r என்க
வட்டகோணப்பகுதியின் சுற்றளவு = l + 2r

கேள்வி 9.
ஒரு விமானத்தை இயக்கும் முன்தள்ளி ஒரு ! நிமிடத்திற்கு 1000 முறை கழல்கிறது. முன் தள்ளியின் முனைப்புள்ளி சுழல்கின்றபோது ஒரு விநாடிக்கு எத்துனை பாகைகள் கிடைக்கும் என்பதைக் காண்க.
தீர்வு:
ஒரு முழு சுற்று = 360°
1 நிமிடத்தில் நகரும் கோணம் = 360° × 1000
60° விநாடிகளில் நகரும் கோணம் = 360° × 1000

கேள்வி 10.
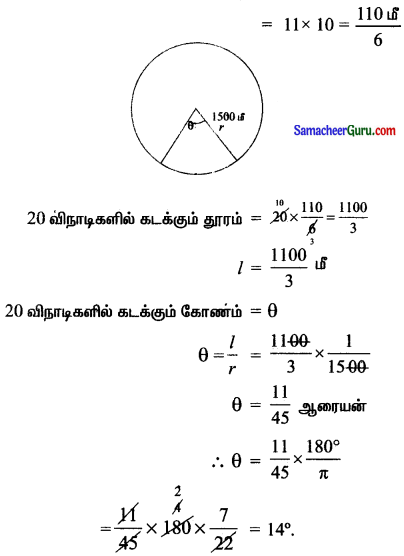
66 கி.மீ/மணி நேர வேகத்தில் 1500 மீ. ஆரம் கொண்ட ஒரு வட்டப் பாதையில் ஒரு தொடர்வண்டி இயக்கப்படுகிறது எனில், 20 நிமிடத்தில் அது கடக்கும் கோணத்தைக் காண்க.
தீர்வு:
1 மணி நேரத்தில் தொடர்வண்டி கடக்கும் தூரம் =66 கி.மீ.
⇒ (60 × 60) விநாடிகளில் கடக்கும் தூரம் = 66 கி.மீ.
1 கி.மீ. = 1000 மீ.
⇒ 1 விநாடியில் கடக்கும் காரம் = \(\frac{66 \times 1000}{60 \times 60}\)

கேள்வி 11.
8 செ.மீ. ஆரம் மற்றும் 6 மி.மீ. தடிமன் கொண்ட ஒரு வட்ட வடிவ உலோகத் தட்டினை உருக்கி, 16 செ.மீ. ஆரம் மற்றும் 4 மி.மீ . தடிமன் உடைய ஒரு வட்டக் கோணப் பகுதியை உருவாக்கினால் அவ்வட்டக் கோணப் பகுதியின் கோண அளவை காண்க.
தீர்வு:
வட்ட வடிவ தகட்டின் ஆரம் = 8 செ.மீ. ;
தடிமன் = 6 மி.மீ.
= \(\frac{6}{10}\) செ.மீ.
உருளையின் கன அளவு = πr²h
வட்ட கோணப் பகுதியின் கன அளவு = \(\frac{\theta}{360}\) πr²h