Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.4 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.4

கேள்வி 1.
0 < x < \(\frac{\pi}{2}\), 0 < y < \(\frac{\pi}{2}\), sin x = \(\frac{15}{17}\), மற்றும் cos y = \(\frac{12}{13}\),
(i) sin (x + y)
(ii) cos (x – y)
(iii) tan (x + y)
ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு:
0 < x < \(\frac{\pi}{2}\), 0 < y < \(\frac{\pi}{2}\)
(x, y) I கால் பகுதியில் அமைவதால் இவை அனைத்து முக்கோணவியல் விகிதங்களும் மிகையாகும்

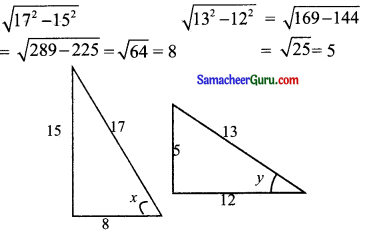
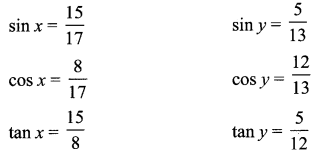
(i) sin (x + y) = sin x cos y + cos x sin y
\(=\frac{15}{17} \times \frac{12}{13}+\frac{8}{17} \times \frac{5}{13}=\frac{180}{221}+\frac{40}{221}=\frac{220}{221}\)

(ii) cos (x – y) = cos x cos y + sin x sin y
\(=\frac{8}{17} \times \frac{12}{13}+\frac{15}{17} \times \frac{5}{13}=\frac{96}{221}+\frac{75}{221}=\frac{171}{221}\)

(iii) tan (x + y)

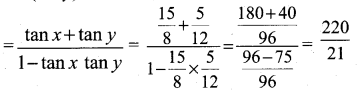
கேள்வி 2.
0 < A < \(\frac{\pi}{2}\), 0 < B < \(\frac{\pi}{2}\), sin A = \(\frac{3}{5}\) மற்றும்
cos B = \(\frac{9}{41}\) எனில் (i) sin (A+ B) (ii) cos (A – B) ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு:
0 < A < \(\frac{\pi}{2}\), 0 < B < \(\frac{\pi}{2}\)
A, B, முதல் கால் பகுதியில் அமைவன.
∴ அனைத்து முக்கோண விகிதங்களும் மிகையாகும்.

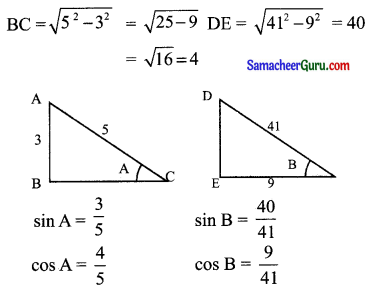
(i) sin (A + B) = sin A cos B + cos A sin B
= \(\frac{3}{5} \times \frac{9}{41}+\frac{4}{5} \times \frac{40}{41}\)
= \(\frac{27}{205}+\frac{160}{205}=\frac{187}{205}\)

(ii) cos (A – B) = cos A cos B + sin A sin B
= \(\frac{4}{5} \times \frac{9}{41}+\frac{3}{5} \times \frac{40}{41}=\frac{36}{205}+\frac{120}{205}=\frac{156}{205}\)

கேள்வி 3.
cos x = \(\frac{-4}{5}\), π < x < \(\frac{3 \pi}{2}\) மற்றும் sin y = \(\frac{-24}{25}\), π < y < \(\frac{3 \pi}{2}\) எனில் cos (x – y) இன் மதிப்பைக்
காண்க.
தீர்வு:
π < x < \(\frac{3 \pi}{2}\), x, III-ம் கால் பகுதியில் அமைவதால் cot x, tan x மிகையாகும்.
π < y < \(\frac{3 \pi}{2}\), y-ம் III-ம் கால் பகுதியில் அமைவதால்
cot y, tan y மட்டுமே மிகையாகும்.

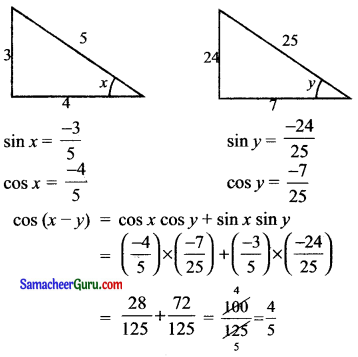
கேள்வி 4.
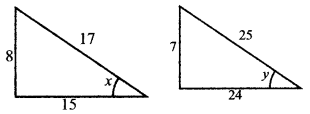
sin x = \(\frac{8}{17}\), 0 < x < \(\frac{\pi}{2}\) மற்றும் cos y = π < y < \(\frac{3 \pi}{2}\) எனில் sin (x-y) இன் மதிப்பை காண்க
தீர்வு:
0 < x < \(\frac{\pi}{2}\), x முதல் கால் பகுதியில் அமைவதால் அனைத்து முக்கோணவியல் விகிதங்களும் மிகையாகும்.

π < y < \(\frac{3 \pi}{2}\), y ஆனது IIIவது கால் பகுதியில் அமைவதால் tan y, cot y மட்டுமே மிகையாகும்.

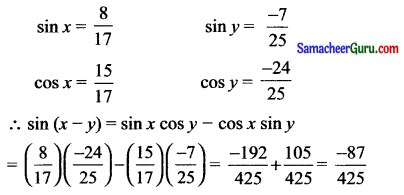
கேள்வி 5.
(i) cos 105°
(ii) sin 105°
(iii) tan \(\frac{7 \pi}{12}\) ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு:
(i) cos 105° = cos (60° + 45°)
= cos 60°. cos 45° – sin 60° sin 45°
= \(\frac{1}{2} \cdot \frac{1}{\sqrt{2}}-\frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{2}}=\frac{1-\sqrt{3}}{2 \sqrt{2}}\)

(ii) sin 150° = sin (60° +45°).
= sin 60° . cos 45° + cos 60° sin 45°
= \(\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{2}}+\frac{1}{2} \times \frac{1}{\sqrt{2}}=\frac{\sqrt{3}+1}{2 \sqrt{2}}\)

(iii)

கேள்வி 6.
நிறுவுக
(i) cos (30° + x) = \(\frac{\sqrt{3} \cos x-\sin x}{2}\)
(ii) cos (π + θ) = – cos θ
(iii) sin (π + θ) = – sin θ
தீர்வு:
(i) cos (30° + x) = \(\frac{\sqrt{3} \cos x-\sin x}{2}\) .
cos(30° + x) = cos 30° . cos x – sin 30 . sin x
= \(\frac{\sqrt{3}}{2}\) cos x – \(\frac{1}{2}\)
sin x = \(\frac{\sqrt{3} \cos x-\sin x}{2}\)
∴ எனவே நிரூபிக்கப்பட்டது

(ii) cos (π + θ) = – cos θ
L.H.S = cos (π + θ) = -cos θ = RHS
எனவே நிரூபிக்கப்பட்டது

(iii) sin (π + θ) = -sin θ
sin (A + B) = sin A cos B + cos A sin B
sin (π + θ) = sin π cos θ + cos π.sin θ
= 0.cos θ + (-1) sin θ
∴ sin (π + θ) = -sin θ
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 7.
sin 15° மற்றும் cos 15° ஆகியவற்றை மூலங்களாகக்
கொண்ட இருபடிச் சமன்பாட்டைக் காண்க.
தீர்வு:
மூலங்களின் கூடுதல் = sin 15° + cos 15°
= sin (45° -30°) + cos (45° -30°)
= sin 45° cos 30° – cos 45° sin 30° + cos 45° – cos 30° + sin 45°. sin 30°

மூலங்களின் பெருக்கற்பலன் = sin 15°.cos 15°
= \(\frac{2 \sin 15^{\circ} \cos 15^{\circ}}{2}=\frac{\sin 30^{\circ}}{2}\) = \(\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\) (∵ sin 2A = 2 sin A cos A)
∴ தேவையான சமன்பாடு
⇒ x² – (மூலங்களின் பெருக்கற்பலன்)
x + (மூலங்களின் பெருக்கற்பலன்) = 0
⇒ x² – \(\left(\frac{\sqrt{6}}{2}\right)\)x + \(\frac{1}{4}\) = 0 ⇒ x² – \(\frac{\sqrt{6}}{2}\)x + \(\frac{1}{4}\) = 0
⇒ 4x² – 2√6 + 1 = 0.

கேள்வி 8.
cos (A + B + C) -ஐ விபிவா க்கு. இங்கு A + B + C = \(\frac{\pi}{2}\) எனில், cos A cos B cos C = sin A sin B cos C + sin B sin C cos A + sin C sin A cos B என நிறுவுக.
தீர்வு:
A + B + C = \(\frac{\pi}{2}\)
⇒ cos(A + B + C) = cos \(\frac{\pi}{2}\)
⇒ cos (A + B + C) = 0
cos (A + B + C) = cos (A + B) cos C – sin (A + B) sin C
= cos C (cos A cos B – sin A sin B) – sin C (sin A cos B + cos A sin B)
= cos A cos B cos C – sin A sin B cos C – sin A cos B sin C – cos A sin B sin C
0 = cos A cos B cos C – sin A sin B cos C – sin A cos B sin C – cos A sin B sin C .
∴ cos A cos B cos. C = sin A sin B cos C + sin A cos B sin C + cos A sin B sin C
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 9.
நிறுவுக.
(i) sin (45° + θ) – sin (45° – θ) = V2 sin θ
(ii) sin (30° + θ) + cos (60° + θ) = cos θ
தீர்வு:
(i) LHS = (sin 45° + θ) – sin (45° – θ)
= sin45°. cos ° + cos 45° sin θ – [sin 45°. cos θ – cos 45° sin θ]

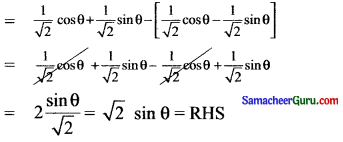
(ii) LHS = sin (30° + θ) + cos (60° + θ)
= sin 30° . cos θ + cos 30° . sin θ + cos 60°. cos θ – sin 60°. sin θ

கேள்வி 10.
a cos (x + y) = b cos (x – y) எனில் (a + b) tan x = (a – b) cot y எனக் கான்பி.
தீர்வு:
a cos (x + y) = b cos (x – y)
⇒ a [cos x cos y – sin x sin y] = b [cos x cos y + sin x sin y]
⇒ a cos x cos y – a sin x sin y = b cos x cos y + b sin x sin y
⇒ (a – b) [cos x cos y] = (a + b)(sin x sin y]
⇒ (a – b) \(\frac{\cos y}{\sin y}\) = (a + b) \(\frac{\sin x}{\cos x}\)
⇒ (a – b) cot y =(a + b) tan x
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 11.
நிறுவுக. sin 105° + cos 105° = cos 45°
தீர்வு:
LHS = sin 105° + cos 105°
= sin (60° + 45°) + cos (60° + 45°)
= sin 60° cos 45° + cos 60° sin 45 + cos 60° cos 45° – sin 60° sin 45°

கேள்வி 12.
நிறுவுக. sin 75° – sin 15° = cos 105° + cos 15°
தீர்வு:
L.H.S = sin 75° – sin 150
= sin (90° – 159) – sin 15°
= cos 15° – sin 15°

R.H.S = cos 105° + cos 15°
= cos (90° + 15°) + cos 15°
= – sin 15° + cos 15°
= cos 15° – sin 15°
∴ R.H.S = L.H.S.

கேள்வி 13.
நிறுவுக. tan 75° + cot 75° = 4
தீர்வு:


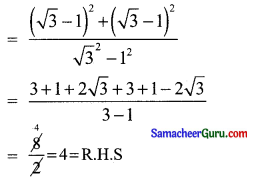
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 14.
நிறுவுக. cos (A + B) cos C – cos (B + C) cos A = sin B sin (C – A)
தீர்வு:
L.H.S = cos (A + B) cos C – cos (B + C) cos A
= (cos A cos B – sin A sin B) cos C – [cos B cos C – sin B sin C]

= cos A sin B sin C – sin A sin B cos C
= sin B [cos A sin C – sin A cos C]
= sin B [sin (C – A] = R.H.S.

கேள்வி 15.
நிறுவுக. sin (n + 1)θ sin (n – 1) θ + cos (n + 1) θ
cos (n – 1) θ = cos 2 θ, n ∈ Z.
தீர்வு:
L.H.S = sin (n + 1) θ sin (n – 1) θ + cos (n + 1) θ cos (n – 1)θ, n ∈ Z
= cos ((n + 1)θ – (n – 1)θ]
[∵ cos (A – B) = cos A cos B + sin A sin B A = (n + 1)θ B = (n – 1) θ]

= cos 2θ = R.H.S
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 16.
x cos θ = y cos (θ + \(\frac{2 \pi}{3}\)) = z cos(θ + \(\frac{4 \pi}{3}\)) எனில், xy + yz + zx இன் மதிப்பைக் கான்க.
தீர்வு:

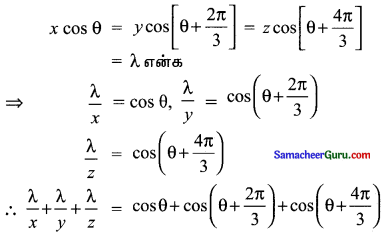
= cos θ + cos (120 + θ) + cos (240 + θ)
= cos θ + cos 120. cos θ – sin 120 . sin θ + cos 240. cos θ – sin 240. sin θ
= cos θ – cos 60° cos θ – sin 60°. sin θ – sin 30° cos θ + cos 30° sin θ
(∵ cos (A + B) = cos A cos B – sin A sin B)
cos 120° = cos (180° – 60°) = -cos 60° = –\(\frac{1}{2}\)
=sin 240° = sin (270° – 30°) = – sin 30°
= – cos 60° = –\(\frac{1}{2}\).

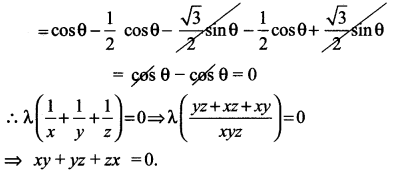
கேள்வி 17.
நிறுவுக.
(i) sin (A + B) sin (A – B) = sin²A – sin²B.
(ii) cos(A + B) cos(A-B) = cos²A – sin²B
= cos² B – sin²A
(iii) sin²(A + B) – sin²(A – B) = sin 2A sin 2B
(iv) cos 8 θ cos 2 θ = cos² 5θ sin² 3θ
தீர்வு:
(i) L.H.S = sin (A + B) sin (A – B)
= [sin A cos B + cos A sin B]. [sin A cos B – cos A sin B]
= sin² A. cos² B – cos² A. sin² B [∵ (a + b)(a – b) = a² – b²]
= sin²A [1 – sin² B] – (1 – sin² A) sin²B
= sin² A – sin² A sin² B – [sin² B – sin² A sin² B]

= sinA – sin?B=R.H.S எனவே நிரூபிக்கப்பட்டது.

(ii) L.H.S = cos (A + B). cos (A – B)
=(cos A cos B – sin A sin B) (cos A cos B + sin A sin B)
= cos² A cos² B – sin² A sin² B …. (1)
= cos² A (1 – sin² B) – (1 – cos² A) sin² B

= cos² A – sin² B …(2)
(1) லிருந்து
LHS = cos² A cos² B – sin² A sin² B
= (1 – sin² A) cos² B – sin² A (1 – cos² B)

= cos² B – sin² A
(2), (3) லிருந்து ..(3)
cos (A + B) cos (A – B) = cos² A – sin² B
= cos² B – sin²A எனவே நிரூபிக்கப்பட்டது

(iii) sin² (A + B) – sin² (A – B) = sin 2A. sin 2B
L.H.S = sin² (A + B) – sin² (A – B)

= sin (2A). sin (2B) (∵ (i) ஐ பபண்படுத்தி)
= RHS எனவே நிரூபிக்கப்பட்டது.

(iv) cos 8θ cos 2θ = cos² 5θ . sin² 3θ
R.H.S = cos² 5θ . sin² 3θ
= cos (5θ + 3θ) cos (5θ – 3θ) (∵ (ii) லிருந்து)
= cos 8θ. cos 2θ = L.H.S cos² B – sin² A
= cos (A + B). cos (A – B)
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 18.
cos² A + cos² B – 2cos A cos B cos (A + B) = sin² (A + B) எனக் கான்பி.
தீர்வு:
LHS = cos² A + (1 – sin²B)2 cos A cos B. cos(A + B)
= cos² A – sin² B + 1 – 2 cos A cos B. cos(A + B)
= cos (A + B). cos (A – B) + 1 – 2 cos A cos B. cos (A + B))
(∵ cos²A – sin²B = cos(A + B) cos (A – B)
= cos (A + B) (cos (A – B) – 2 cos A cos B] + 1
= – cos (A + B) [cos A cos B – sin A sin B] + 1
= – cos (A + B) cos (A + B) + 1
= – cos²(A + B) + 1 = 1 – cos² (A + B)
= sin² (A + B) = R.H.S எனவே நிரூபிக்கப்பட்டது.

கேள்வி 19.
cos (α – β)+ cos (β – γ) + cos (γ – α) = \(\frac{-3}{2}\) எனில் cos α + cos β + cos γ = sin α + sin β + sin γ = 0 எனக் காண்பி.
தீர்வு:
cos (α – β) + cos (β – γ) + cos (γ – α) = \(\frac{-3}{2}\)
⇒ cos α cos β + sin α sin β + cos β. cos γ + sin β sin γ
+ cos γ cos α + sin α sin γ = \(\frac{-3}{2}\)
⇒ 2 [cos α cos β + sin α sin β + cos β. cos γ + sin β sin γ + cos γ cos α + sin α sin γ] = -3
⇒ 2 cos α cos β + 2 cos β cos γ + 2 cos γ cos α + 2 sin α sin β + 2 sin β sin γ + 2 sin α sin γ + 3 = 0
⇒ (2 cos α cos β + 2 cos β cos γ + 2 cos γ cos α) + (2 sin α sin β + 2 sin β sin γ + 2 sin α sin γ) + (cos² α + sin² β) + (cos² γ + sin² γ) = 0
⇒ cos² α + cos² β + cos² γ + 2 cos α cos β + 2 cos β cos γ + 2 cos γ cos α + sin² α sin² β + sin² γ + 2 sin α sin β + 2 sin β sin γ + 2 sin γ. sin α = 0
⇒ (cos α + cos β + cos γ)² + (sin α + sin β + sin γ)² = 0
⇒ cos α + cos β + cos γ = 0
⇒ sin α + sin β + sin γ = 0
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 20.
(i) tan (45° + A) = \(\frac{1+\tan A}{1-\tan A}\)
(ii) tan (45° – A)= \(\frac{1-\tan A}{1+\tan A}\)
எனக் காண்பி.
தீர்வு:
(i) L.H.S = tan (45° + A)

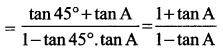
(∵ tan 45° = 1)
எனவே நிரூபிக்கப்பட்டது

(ii) L.H.S = tan (45° – A)

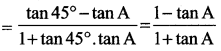
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 21.
நிறுவுக. cot (A + B) = \(\frac{\cot A \cot B-1}{\cot A+\cot B}\)
தீர்வு:
L.H.S = cot (A + B)

நிரூபிக்கப்பட்டது.

கேள்வி 22.
tan x = \(\frac{n}{n+1}\) மற்றும் tan y = \(\frac{1}{2n+1}\) எனில், tan (x + y) ஐக் கான்க.
தீர்வு:


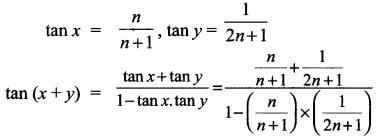
∴ tan (x + y) = 1.

கேள்வி 23.
நிறுவுக. tan (\(\frac{\pi}{4}\) + θ) tan (\(\frac{3 \pi}{4}\) + θ) = -1
தீர்வு:
LHS = tan (\(\frac{\pi}{4}\) + θ) . tan (\(\frac{3 \pi}{4}\) + θ)
= tan(45° + θ). tan(135° + θ)
= tan(45° + θ).tan(180° – 45° + θ)
= tan(45° + θ). tan(180° – (45 – θ))
= tan(45° + θ)(- tan(45° – θ)]
= -tan(45° + θ) tan(45° – θ)

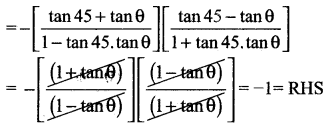
கேள்வி 24.
cat α = \(\frac{1}{2}\), α∈ \(\left(\pi, \frac{3 \pi}{2}\right)\) மற்றும் sec β = –\(\frac{5}{3}\), β ∈\(\left(\frac{\pi}{2}, \pi\right)\) எனில் tan (α + β) இன் மதிப்பைக் காண்க.
தீர்வு:

கேள்வி 25.
θ + Φ = 0 மற்றும் tan θ = k tan θ எனில் sin (θ – Φ) = \(\frac{k-1}{k+1}\) sin α என நிறுவுக.
தீர்வு: