Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.7

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.7 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.7

கேள்வி 1.
A + B + C = 180°, எனில் பின்வருவனவனற நிறுவுக.
(i) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
(ii) cos A + cos B – cos C = -1 + 4 cos A cos B cos C
(iii) sin²A + sin²B + sin²C = 2 + 2 cos A cos B cos C
(iv) sin² A + sin² B – sin² C = 2 sin A sin B cos C
(v) tan\(\frac{A}{2}\) tan\(\frac{B}{2}\) + tan\(\frac{B}{2}\) tan\(\frac{C}{2}\) + tan \(\frac{C}{2}\) tan\(\frac{A}{2}\) = 1
(vi) sin A + sin B + sin C = 4 cos\(\frac{A}{2}\) cos\(\frac{B}{2}\) cos\(\frac{C}{2}\)
(vii) sin(B + C – A) + sin(C + A – B) + sin(A + B – C) = 4 sin A sin B sin C.
தீர்வு:
L.H.S = sin 2A + sin 2B + sin 2c
= 2 sin\(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 2sin C cosC
(∵ sin 2C = 2 sinC cosC)
= 2 sin(A + B)cos(A – B) + 2 sin cosC
(sin C + sin D = 2 sin\(\left(\frac{\mathrm{C}+\mathrm{D}}{2}\right)\) cos\(\left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)\)
= 2sin (180 – C) cos (A + B) + 2 sin cosC
(∵ A + B + C = 180°)
= 2 sinC cos(A – B) + 2 sin C cos C
= 2 sin c [cos(A – B) + cosC]
= 2 sin C (cos(A – B) – cos(A + B)]
= 2 sin C 2 sin A sin B
= 4sin A sin B sin C = RHS
எனவே நிரூபிக்கப்பட்டது.

(ii) LHS = cos A + cos B – cos C

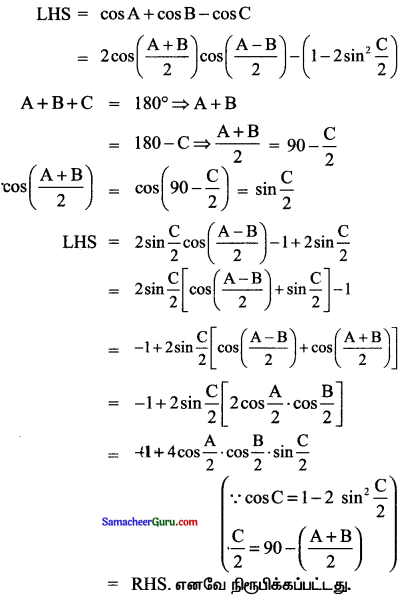
(iii) LHS = sin²A + sin²B + sin²C


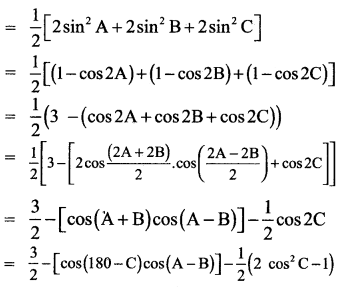
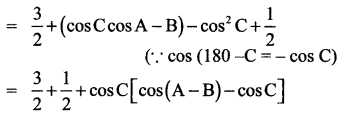
= 2 + cos C[cos(A – B) + cos(A + B)]
= 2 + cos C[2 cos A cos B]
= 2 + 2cos A cos B cos C
= RHS. எனவே நிரூபிக்கப்பட்டது.

(iv) LHS = sin²A + sin²B – sin²C

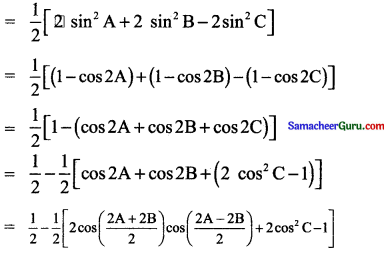
= -(-cos C cos (A – B) – cos²C)
(∵ cos (A + B) = cos (180 – C) = – cos C)
= cos C ∙ cos(A – B) + cos²C
= cos C(cos(A – B) + cos C]
= cos C(cos(A – B) – cos(A + B)]
= cos C(2 sin A sin B)
= RHS. எனவே நிரூபிக்கப்பட்டது.

(v) A + B + C = 180
A + B = 180 – C

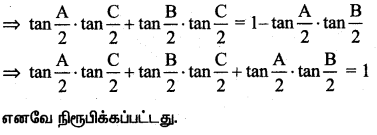
(vi)

(vii) LHS = sin (B + C – A) + sin (C + A – B) + sin (A + B – C)
= sin (180 – A – A) + sin (180 – B – B) + sin (180 – C – C)
= sin (180 – 2A) + sin (180 – 2B) + sin (180 – 2C)
= sin 2A + sin 2B + sin 2C
= 2 sin\(\)cos\(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 2 sin C cos C
= 2 sin(A + B).cos(A – B) + 2 sinC cosC
= 2 sin C [cos (A – B) + cos C (A + B = C = 180°)
= 2 sin C [cos (A – B) + cos (180°- (A + B))
= 2 sin C (cos(A – B) – cos(A + B)]
= 2 sin C2 sin A sin B = 4 sin A sin B sin C
= RHS. எனவே நிரூபிக்கப்பட்டது.

கேள்வி 2.
A + B + C = 2s எனில், sin (s – A) sin (s – B) + sin s sin (s – C) = sin A sin B என நிறுவுக.
தீர்வு:
A + B + C = 2s கொடுக்கப்பட்டுள்ளது
L.H.S = sin (s – A) sin (s – B) + sin s.sin (s-C)
= \(\frac{1}{2}\)[cos(s – A – s + B) – cos(s – A + s – B)] + \(\frac{1}{2}\)[cos(s – s + C) – cos(s + s – C)]
(∵ sin A sin B = \(\frac{1}{2}\)(cos(A – B) – cos(A + B))
= \(\frac{1}{2}\)(cos(A – B) – cos(2s – A – B) + cos C – cos(2s – C)
= \(\frac{1}{2}\)(cos(A – B) – cosC + cosC – cos(A+B) (∵ 2s = A + B + C)

= sin A ∙ sin B = RHS.
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 3.
x + y + z = xyz எனில், \(\frac{2 x}{1-x^{2}}+\frac{2 y}{1-y^{2}}+\frac{2 z}{1-z^{2}}\) = \(\frac{2 x}{1-x^{2}} \cdot \frac{2 y}{1-y^{2}} \cdot \frac{2 z}{1-z^{2}}\) என நிறுவுக.
தீர்வு:
x = tan A, y = tan B, z = tan
x + y + z = xyz = 0
⇒ tan A + tan B + tan C – tan A tan B tan C = 0

⇒ tan(A + B) + tan C = 0

⇒ tan A + tan B + tan C 1- tan A-tan +tan C = 0
⇒ tan A + tan B + tan C – tan A tan B tan C = 0
⇒ tan A + tan B + tan C = tan A . tan B. tan C = 0 …..(1)
⇒ tan A + tan B + tan C – tan A. tan B. tan C = 0
⇒ tan (A + B + C) = 0
⇒ tan 2 (A + B + C) = 0
⇒ tan (2A + 2B + 2C) = 0
⇒ tan 2A + tan 2B + tan 2C = tan 2A tan 2B tan 2C (1) -ன் படி

கேள்வி 4.
A + B + C = \(\frac{\pi}{2}\) எனில், பின்வருவனவற்றை நிறுவுக.
(i) sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C
(ii) cos 2A+cos 2B+ cos 2C = 1 + 4 sin A sin B sin C
தீர்வு:
A + B + C = \(\frac{\pi}{2}\)

(i) L.H.S = sin 2A + sin 2B + sin 2C

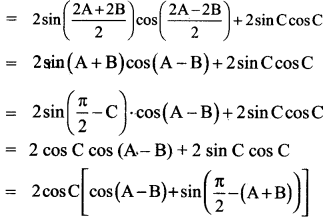
= 2 cos C (cos (A – B) + cos (A + B)]
= 2 cos C. 2 cos A. cos B
= 4 cos A cos B cos C = R.H.S.
எனவே நிரூபிக்கப்பட்டது.

(ii) L.H.S = cos 2A+ cos 2B + cos 2C


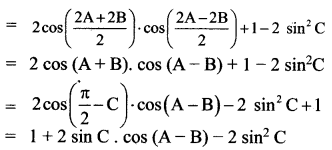
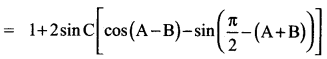
= 1 + 2 sin C [cos (A – B) – cos (A + B)]
= 1 + 2 sin C [2 sin A. sin B]
= 1 + 4 sin A sin Bsin C = R.H.S.
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 5.
∆ ABC ஒரு செங்கோண முக்கோணம் மற்றும் ∠A = \(\frac{\pi}{2}\) எனில், பின்வருவனவற்றை நிறுவுக.
(i) cos² B + cos² C = 1
(ii) sin² B + sin² C = 1
(iii) cos B – cos C = -1 + 2√2cos\(\frac{\mathrm{B}}{2}\) sin\(\frac{\mathrm{C}}{2}\)
தீர்வு:
(i)

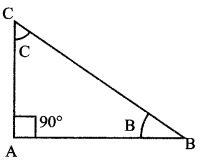
∠A = \(\frac{\pi}{2}\), B + C = \(\frac{\pi}{2}\)
L.H.S = cos² B + cos² C
= cos²B + \(\left[\cos \left(\frac{\pi}{2}-\mathrm{B}\right)\right]^{2}\)
= cos² B + sin² B = 1 = RHS.
எனவே நிரூபிக்கப்பட்டது.

(ii) L.H.S = sin² B + sin² C

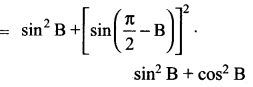
= sin² B + cos² B = 1 = RHS.
எனவே நிரூபிக்கப்பட்டது.

(iii) cos B – cos C = -1 + 2√2cos\(\frac{\mathrm{B}}{2}\) sin\(\frac{\mathrm{C}}{2}\)
L.H.S = cos B – cos C