Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.8 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.8

கேள்வி 1.
பின்வருவனவற்றுக்கு முதன்மை தீர்வு மற்றும் பொதுத் தீர்வுகளைக் காண்க.
(i) sin θ = – \(\frac{1}{\sqrt{2}}\)
(ii) cot θ = √3
(iii) tan θ = – \(\frac{1}{\sqrt{3}}\)
தீர்வு:
(i) sin θ = – \(\frac{1}{\sqrt{2}}\) கொடுக்கப்பட்டுள்ளது.
sin θ = – \(\frac{1}{\sqrt{2}}\) < 0
எனவே IV-ம் கால் பகுதியால் அமைகிறது.
sin θ = – sin\(\frac{\pi}{4}\) = sin\(\left(\frac{-\pi}{4}\right)\)
θ = \(\frac{\pi}{4}\) என்பது முதன்மைத் தீர்வு ஆகும்.

பொதுத்தீர்வு:
θ = nπ + (-1)ⁿ\(\left(\frac{-\pi}{4}\right)\), n ∈ Z

(ii) cot θ = √3 ⇒ tan θ = \(\frac{-1}{\sqrt{3}}\) < 0
முதன்மைத் தீர்வு 1-ம் கால் பகுதியில் அமையும்.
∴ tan θ = \(\frac{1}{\sqrt{3}}\) = tan \(\left(\frac{\pi}{6}\right)\)
θ = \(\frac{\pi}{6}\) என்பது முதன்மைத் தீர்வு ஆகும்.

பொதுத்தீர்வு:
θ = nπ + \(\frac{\pi}{6}\), n ∈ Z

(iii) tan θ = \(\frac{-1}{\sqrt{3}}\) < 0, θ
-IV-ம் கால் பகுதியில் அமையும்.
tan θ = \(\frac{-1}{\sqrt{3}}\) = – tan\(\frac{\pi}{6}\)
⇒ tan θ = tan\(\left(\frac{-\pi}{6}\right)\)
⇒ θ = \(\frac{-\pi}{6}\) என்பது முதன்மைத் தீர்வு,

பொதுத்தீர்வு:
θ = nπ + \(\left(\frac{-\pi}{6}\right)\), n ∈ Z

கேள்வி 2.
0° < θ < 360° என்ற இடைவெளியில் கீழ்க்கண்ட சமன்பாடுகளுக்கு சரியான தீர்வுகளைக் காண்க.
(i) sin⁴x = sin²x
(ii) 2 cos⁴x + 1 = -3 cos x
(iii) 2 sin²x + 1 = 3 sin x
(iv) cos 2x = 1 – 3 sin x
தீர்வு:
(i) sin⁴x = sin²x
⇒ sin⁴x – sin²x = 0
⇒ sin²x (sin²x – 1) = 0
⇒ sin²x = 0 அல்லது sin²x – 1= 0
⇒ sin x = 0 அல்லது sin²x = 1
⇒ sin x = 0, ± 1 ⇒ x = 0, π ….(1)
⇒ sin x = sin 90°
⇒ x = 90° = \(\frac{\pi}{2}\) …(2)
⇒ sin x = -1
⇒ sin x = – sin\(\frac{\pi}{2}\)
⇒ sin x = sin\(\left(\pi+\frac{\pi}{2}\right)\) (sin மதிப்பு III-ம் கால் பகுதி குறையாகும்)
⇒ sin x = sin \(\frac{3 \pi}{2}\)
⇒ x = \(\frac{3 \pi}{2}\) ……(3)
(1), (2), (3) லிருந்து x = 0, \(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\), π

(ii) 2 cos² x + 1 = -3 cos x
⇒ 2 cos²x + 3 cos x + 1 = 0

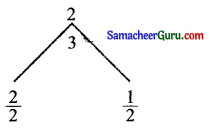
⇒ ( cos x + 1)(2 cos x + 1) =0
⇒ (cos x + 1) = 0 அல்ல து
(2 cos x+ 1) = 0
வகை (i) cos x + 1 = 0
⇒ cos x = – 1
⇒ cos x = – cos 0°
⇒ cos x = cos(π – 0)
⇒ x = π அல்லது cos x = cos(π – 0)
⇒ x = π, π …… (1)
(∴ cos x II, III-ம் கால் பகுதியில் குறையாகும்)
வகை (ii) 2cos x + 1 = 0
⇒ 2 cos x = -1
⇒ cos x = \(\frac{-1}{2}\) = -cos\(\frac{\pi}{3}\)
⇒ cos x = \(\left(\pi+\frac{\pi}{3}\right)\) அல்லது cos x = cos \(\left(\pi-\frac{\pi}{3}\right)\)
(∴ cos X, II, III-ம் கால் பகுதியில் குறை மதிப்புடையது)
⇒ cos x = cos \(\frac{4 \pi}{3}\) அல்லது cos x = cos \(\frac{2 \pi}{3}\)
⇒ θ x = \(\frac{4 \pi}{3}\) அல்லது \(\frac{2 \pi}{3}\) …(2)
(1), (2) லிருந்து x = π, \(\frac{4 \pi}{3}\), \(\frac{2 \pi}{3}\) ஆகும்.

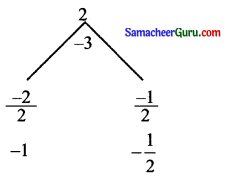
(iii) 2sin²x + 1 = 3 sinx
2sin²x – 3 sinx + 1 = 0
(sin x – 1)(2sin x – 1) = 0

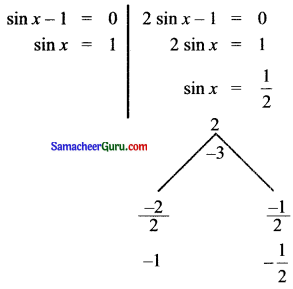
வகை (i) sin x = 1
⇒ sin x = 90
x = \(\frac{\pi}{2}\) …… (1)
வகை (ii) sin x = \(\frac{1}{2}\) ⇒ sin \(\frac{\pi}{6}\)
x = \(\frac{\pi}{6}\) …… (2)
(1), (2) ⇒ x = \(\frac{\pi}{2}\), \(\frac{\pi}{6}\)

(iv) cos 2x = 1 – 3 sin x
cos 2x = 1 – 2 sin²x
⇒ cos 2x = 1 – 3 sinx ⇒ 1 – 2 sin²x
⇒ -2 sin² x = -3 sin x
⇒ 2 sin²x = 3 sin x
⇒ sin x (2 sinx – 3) = 0
⇒ sin x = 0 அல்லது
2 sin x – 3 = 0
2 sin x = 3
sin x = \(\frac{3}{2}\)
வகை (i) sin x = 0
x = 0, π
வகை (ii) sin x = \(\frac{3}{2}\)-ஆக இருக்க முடியாது.
∵ sinx-ன் மதிப்புகள் 1ஐ விட பெரியதாக இருக்க முடியாது.
∴ x-ன் மதிப்புகள் 0, π

கேள்வி 3.
பின்வரும் சமன்பாடுகளைத் தீர்க்கவும்
(i) sin 5x – sinx = cos 3x
தீர்வு:
sin 5x – sin x = cos 3x
⇒ 2 cos\(\left(\frac{5 x+x}{2}\right)\).sin\(\left(\frac{5 x-x}{2}\right)\) = cos 3x
(∵ sin C – sin D = 2 cos \(\frac{\mathrm{C}+\mathrm{D}}{2}\) sin \(\frac{\mathrm{C}-\mathrm{D}}{2}\))
⇒ 2 cos 3x sin 2x = cos 3x
⇒ 2 cos 3x sin 2x – cos 3x = 0
⇒ cos 3x (2 sin 2x – 1) = 0
⇒ cos 3x = 0, அல்லது
2 sin 2x – 1 = 0
2 sin 2x = 1; sin 2x = \(\frac{1}{2}\)

வகை (i) cos 3x = 0
3x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
(∵ cos θ = 0 ⇒ θ = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
⇒ x = (2n + 1)\(\frac{\pi}{6}\), n ∈ Z

வகை (ii)

(ii) 2 cos²θ + 3 sin θ – 3 = 0
தீர்வு:
2 cos²θ + 3 sin θ – 3 = 0

2(1 – sin²θ) + 3 sin θ – 3 = 0
⇒ 2 – 2 sin²θ + 3 sin θ – 3 = 0
⇒ – 2 sin²θ + 3 sin θ – 1 = 0
⇒ 2 sin²θ – 3 sin θ + 1 = 0
⇒ (sin θ – 1) (2 sin θ – 1) = 0
⇒ sin θ = 1 அல்லது sin θ = \(\frac{1}{2}\)

(iii) cos θ + cos 3θ = 2 cos 2θ
தீர்வு:
cos θ + cos 3θ = 2cos 2θ
⇒ 2c0s\(\left(\frac{\theta+3 \theta}{2}\right)\).cos\(\left(\frac{\theta-3 \theta}{2}\right)\) – 2 cos 2θ = 0
(∵ cos C + cos D = 2 cos \(\left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \cdot\left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)\))
⇒ 2 cos 2θ.cos θ – 2cos 2θ = 0
⇒ (cos 2θ)(cos θ – 1) = 0
⇒ cos 2θ = 0 அல்ல து cos θ = 1

வகை (i) cos 2θ = 0
2θ = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
(∵ cos θ = 0 ⇒ θ = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z)

வகை (ii) cos θ = 1
cos θ = cos 0°
θ = 2nπ ± 0, n ∈ Z
θ = 2nπ, n ∈ Z
0-ன் தீர்வுகள் θ = (2n + 1)\(\frac{\pi}{4}\), 2nπ, n ∈ Z

(iv) sin θ + sin 3θ + sin 5θ = 0
தீர்வு:
sin θ + sin 3θ + sin 5θ = 0

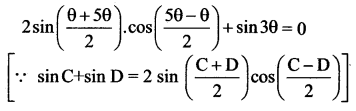
⇒ 2 sin 3θ cos 2θ + sin 3θ = 0
⇒ sin 3θ (2 cos 2θ + 1) = 0
⇒ sin 3θ = 0 அல்லது cos 2θ = \(\frac{-1}{2}\)

வகை (i) sin 3θ = 0
3θ = nπ, n ∈ Z
θ = \(\frac{n \pi}{3}\), n ∈ Z

வகை (ii)

(v) sin 2θ – cos 2θ – sin θ + cos θ = 0
தீர்வு:
sin 2θ – cos 2θ – sin θ + cos θ = 0
⇒ sin 2θ – sin θ + cos θ – cos 2θ = 0

(vi) sin θ + cos θ = √2
தீர்வு:

(vii) sin θ + √3 cos θ = 1
தீர்வு:

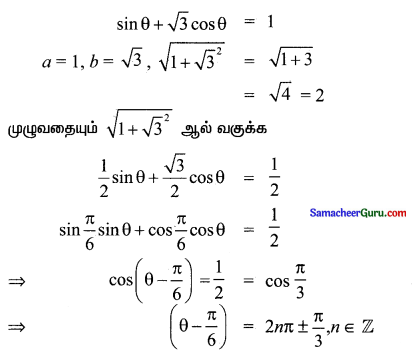
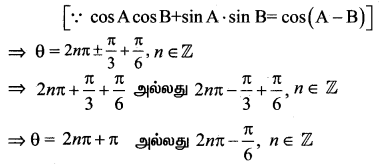
(viii) cot θ + cosec θ = √3
தீர்வு:

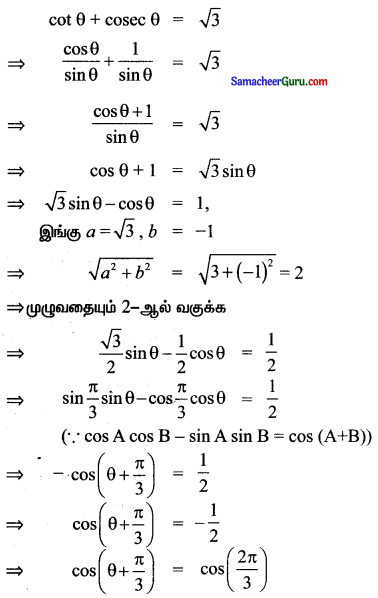
(ix) tan θ + tan \(\left(\theta+\frac{\pi}{3}\right)\) + tan \(\left(\theta+\frac{2\pi}{3}\right)\) = √3
தீர்வு:

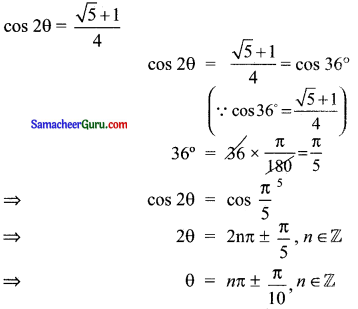
(x) cos 2θ = \(\frac{\sqrt{5}+1}{4}\)
தீர்வு:

(xi) 2 cos²x – 7 cos x + 3 = 0
தீர்வு:
2 cos²x – 7 cos x + 3 = 0
⇒ (cos x – 3) (2 cos x – 1) = 0
⇒ (cos x – 3) = (0)
⇒ cos x = 3
⇒ அல்லது (2 cosx – 1) = 0
⇒ cos x = \(\frac{1}{2}\)
cos x= 3-ஆக இருக்க முடியாது

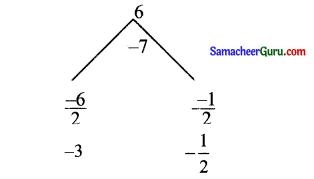
∴ cos x = \(\frac{1}{2}\)
⇒ cos x = cos \(\frac{\pi}{3}\)
⇒ x = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z
∴ x-ன் தீர்வு = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z