Samacheer Kalvi 11th Maths Guide Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.9

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.9 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 3 அடிப்படை இயற்கணிதம் Ex 3.9

கேள்வி 1.
∆ABC இல் \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\) எனில், a², b², c² ஆகியவை ஒரு கூட்டுத் தொடர் வரிசையில் அமையும் என நிறுவுக.
தீர்வு:

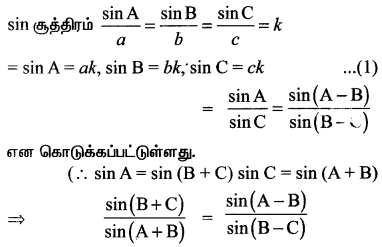
⇒ sin (B + C) ∙ sin (B – C) = sin(A + B) sin(A – B)
⇒ sin²B – sin²c = sin²A- sin²B
⇒ k²b² – k²c² = k²a² – k²b²
⇒ b² – c2 = a² – b²
⇒ 2b² = a² + c²
⇒ a², b², c² ஒரு கூட்டுத் தொடர்.

கேள்வி 2.
∆ABC இன் கோணங்கள் ஒரு கூட்டுத் தொடர் வரிசையில் அமையும் மற்றும் b : c = √3: √2 எனில், ∠A ஐக் காண்க.
தீர்வு:
∠A, ∠B, ∠C என்பது ஒரு கூட்டுத் தொடர் வரிசையில் அமையும்.
∴ 2∠B = ∠A + ∠C
⇒ 3∠B = ∠A + ∠B + ∠C
இருபுறமும் ZB ஐக் கூட்ட
⇒ 3 ∠B = 180°

⇒ ∠C = 45°
∠A = 180 – (∠B + ∠C)
= 180 – (60 + 45) = 75°
∠A = 75°, ∠B = 60°, ∠C = 45°

கேள்வி 3.
∆ABC இல் cos C = \(\frac{\sin A}{2 \sin B}\) எனில், ஒரு இருசமபக்க முக்கோணம் எனக் காண்பி.
தீர்வு:

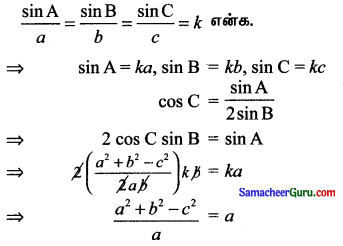
⇒ a² + b² – c² = a²
⇒ b² – c² = 0
⇒ b² = c²
⇒ b = c
∴ ∆ ABC ஓர் இருசமபக்க முக்கோணம்.

கேள்வி4.
∆ABC இல் \(\frac{\sin B}{\sin C}=\frac{c-a \cos B}{b-a \cos C}\) என நிறுவுக.
தீர்வு:

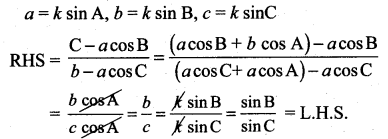
கேள்வி 5.
∆ABC இல் a cos A + b cos B + c cos C = 2a sin B sin C என நிறுவுக.
தீர்வு:

a = k sin A, b = k sin B, c = k sin C … (1)
L.H.S = a cos A + b cos B+c cos C
(1) லிருந்து ⇒ k sin A cos A + k sin B cos B + k sin C cos C
= \(\frac{k}{2}\) [2 sin A cos A + 2 sin B cos B + 2 sin C cos C]
= \(\frac{k}{2}\) [sin 2A + sin 2B + sin 2C]

= 2 (k sin A) sin B sin C
= 2 a sin B sin C ⇒ R.H.S.
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
∆ABC இல் ∠A = 60° b + c = 2a cos\(\left(\frac{B-C}{2}\right)\) என நிறுவுக.
தீர்வு:
A + B + C = 180°.
⇒ B + C = 180 – A = 180° – 60° = 120°
⇒ \(\frac{\mathrm{B}+\mathrm{C}}{2}\) = 60° …(1)
எனவே sin சூத்திரத்தைப் பயன்படுத்தி


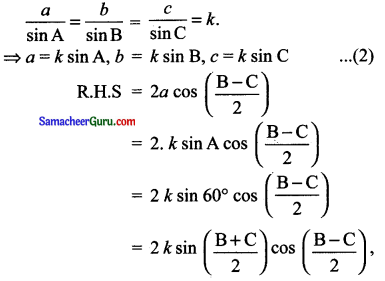
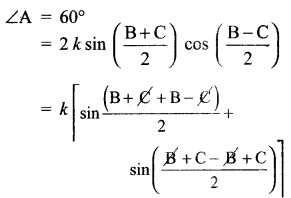
= k [sin B + sin C]
[∵2 sin A cos B = sin (A + B) sin (A – B)]
= k sin B + k sin C
= b + c . [(2) – ல் இருந்து]
= L.H.S. எனவே நிரூபிக்கப்பட்டது.

கேள்வி 7.
∆ABC இல் பின்வன வற்றை நிறுவுக.
(i) a sin \(\left(\frac{\mathbf{A}}{2}+\mathbf{B}\right)\)= (b + c) sin \(\frac{\mathrm{A}}{2}\)
தீர்வு:

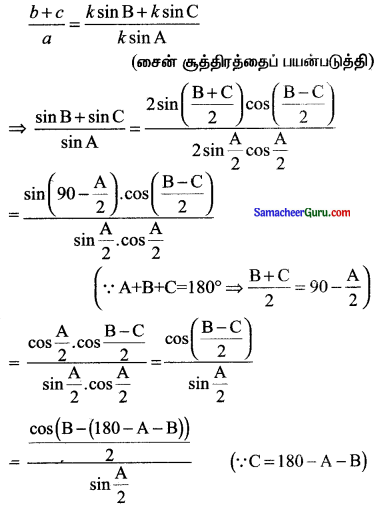
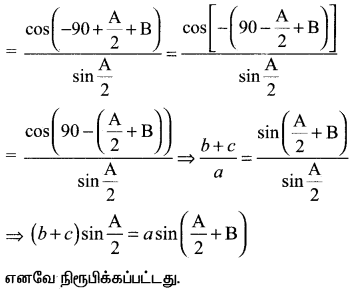
(ii) a (cos B + cos C) = 2 (b + c) sin² \(\frac{\mathrm{A}}{2}\)
தீர்வு:

(iii) \(\frac{a^{2}-c^{2}}{b^{2}}=\frac{\sin (A-C)}{\sin (A+C)}\)
தீர்வு:

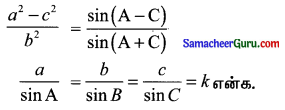
(iv) \(\frac{a \sin (\mathrm{B}-\mathrm{C})}{b^{2}-c^{2}}=\frac{b \sin (\mathrm{C}-\mathrm{A})}{c^{2}-a^{2}}=\frac{c \sin (\mathrm{A}-\mathrm{B})}{a^{2}-b^{2}}\)
தீர்வு:

(v) \(\frac{a+b}{a-b}=\tan \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cot \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)\)
தீர்வு:

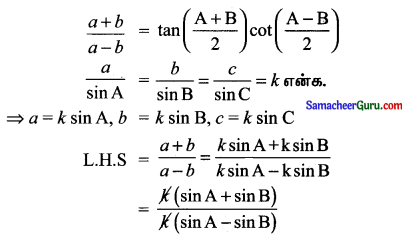
கேள்வி 8.
∆ABC இல் (a² – b² + c) tan B = (a² + b² – c²) tan C என நிறுவுக.
தர்வு:

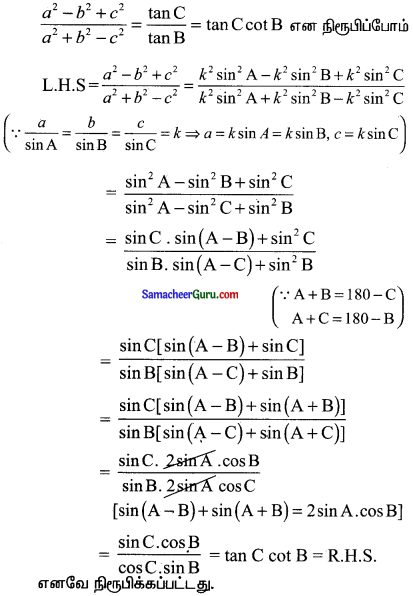
கேள்வி 9.
ஒரு கிராமத்தில் ஒரு பொறியாளர் 120 மீ சுற்றளவுள்ள முக்கோண வடிவ பூங்காவை வடிவமைக்க முனைகிறார். பூங்காவின் பரப்பு அதிகபட்சமாக இருக்கும்படி அமைக்கப்படும்போது அதன் பக்க அளவுகளைக் காண்க.
தீர்வு:
நிலையான சுற்றளவு கொண்ட சமபக்க முக்கோணத்தின் பரப்பு மீப்பெரு மதிப்பாகும்.
சமபக்க ∆-ன் பக்கம் = a என்க
சுற்றளவு = 120 மீ.
⇒ a + a + a = 120 மீ.
3a = 120 மீ.
a = 40 மீ.
பூங்காவின் பக்கம் = 40 மீ.

கேள்வி 10.
12 மீ நீளமுள்ள ஒரு கயிறு கொடுக்கப்பட்டு அதைக்
கொண்டு அதிகபட்சப் பரப்புடைய முக்கோணம் அமைக்கப்பட்டால் அதன் பக்க அளவுகளைக் காண்க.
தீர்வு:
கயிற்றின் நீளம் = 12 மீ.
முக்கோணத்தின் சுற்றளவு = 12 மீ.
நிலையான சுற்றளவு கொண்ட சமபக்க ∆-ன் பரப்பு மீப்பெரு மதிப்பாகும். சமபக்க ∆-ன் பக்கம் = a என்க.

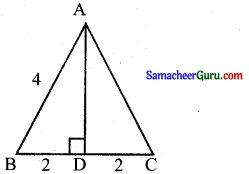
a + a + a =12
3a = 12
a = 4 மீ.

கேள்வி 11.
(i) சைன் விதி
(ii) கொசைன் விதி ஆகியவைகளைப் பயன்படுத்தி வீழல் சூத்திரத்தை வருவி.
தீர்வு:
(i) சைன் விதி \(\frac{a}{\sin \mathrm{A}}=\frac{b}{\sin \mathrm{B}}=\frac{c}{\sin \mathrm{C}}\) = k
a = k sin A, b = k sin B, c = k sin C.
a = b cos C + c cos B, b = c cos A + a cos C
c = a cos B + b cos A
a = b cos C + c cos B ஐ நிரூபிக்க
R.H.S = b cos C + c cos B
= k sin B cos C + k sin C cos B
= k (sin B cos C + sin C cos B)
= k sin (B + C)
= k sin (180 – A) (∵ A + B + C = 180°)
= sin A = a = L.H.S
b = c cos A + a cos C,
c = a cos B + b cos A என நிரூபிக்கலாம்.

(ii) கொசைன் விதி:
R.H.S = b cos C + cos B.

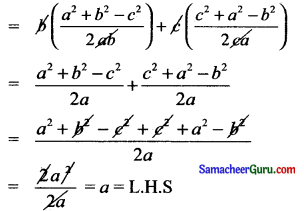
எனவே நிரூபிக்கப்பட்டது.