Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 சேர்ப்பியல் மற்றும் கணிதத் தொகுத்தறிதல் Ex 4.1 Textbook Questions and Answers, Notes.
TN Board 11th Maths Solutions Chapter 4 சேர்ப்பியல் மற்றும் கணிதத் தொகுத்தறிதல் Ex 4.1
கேள்வி 1.
(i) ஒருவர் இரவு விருந்திற்காக ஒரு உணவு விடுதிக்கு சென்றார். அங்கிருந்த உணவு பட்டியலில் 10 இந்திய மற்றும் 7 சீன உணவு வகைகள் இருந்தன. ஒரு இந்திய அல்லது ஒரு சீன உணவை அவர் எத்தனை வகைகளில் தேர்ந்தெடுக்க முடியும்?
தீர்வ:
ஒருவர் 10 இந்திய உணவை 10 வழியிலும் 7 சீன உணவை 7 வழியிலும் தேர்வு செய்ய முடியும்.
ஃ கூட்டுதலின் அடிப்படைக் கொள்கையின்படி 10 – இந்தியன் மற்றும் 7 சீன உணவை (10 + 7) = 17 வழிகளில் தேர்வு செய்யலாம்.
(ii) ஓர் கடையில் 3 விதிமான மகிழுந்து பொம்மைகளும், 2 விதமான தொடர் வண்டி பொம்மைகளும் உள்ளன. ஒரு குழந்தை ஒரு மகிழுந்து பொம்மையையும் மற்றும் ஒரு தொடர் வண்டி பொம்மையையும் எத்தனை வழிகளில் தேர்ந்தெடுக்கலாம்?
தீர்வ:
3 விதமான மகிழுந்து பொம்மைகளை = 3 வழிகளில் வாங்கலாம்.
2 விதமான தொடர்வண்டி பொம்மைகளை = 2 வழிகளில் வாங்கலாம். பெருக்கலின் அடிப்படைக்கொள்கையின்படி = (3 × 2) = 6 வழிகளில் வாங்கலாம்.
![]()
(iii) 1, 2, 3, 4, 5 என்ற இலக்கங்களை திரும்ப வராத முறையில் பயன்படுத்தி எத்தனை இரண்டு – இலக்க எண்களை உருவாக்கலாம்?
தீர்வ:
| பத்துகள் | ஒன்றுகள் |
| 4 | 5 |
ஒன்றாவது இடத்தை 1,2,3,4,5 என்ற எண்களைப் பயன்படுத்தி 5 வழிகளில் நிரப்பலாம்.
பத்தாவது இடத்தை 4 வழிகளில் நிரப்பலாம்.
∴ இரண்டு இலக்க எண்களை (எந்த எண்ணும் திரும்ப வராத முறையில் 4 × 5 = 20 வழிகளில் நிரப்பலாம்.
(iv) 10 இருக்கைகள் உள்ள அரங்கில் மூன்று நபர்கள் நுழைகிறார்கள். எத்தனை வழிகளில் அவர்கள் அந்த இருக்கையில் அமரலாம்?
தீர்வ:
முதல் மனிதர் ஒரு இருக்கையில் = 10 வழிகளில்
அமரலாம் இரண்டாவது மனிதர் ஒரு இருக்கையில் = 9 வழிகளில் அமரலாம் மூன்றாவது மனிதர் ஒரு இருக்கையில் = 8 வழிகளில் அமரலாம்.
∴ பெருக்கலின் அடிப்படைக் கொள்கையின்படி மூன்று மனிதர்கள் = 10 × 9 × 8 = 720 வழிகளில் அமரலாம்.
(v) 5 நபர்களை ஒரு வரிசையில் எத்தனை வழிகளில் அமர வைக்கலாம்?
தீர்வ:
5 நபர்களை அமர வைக்க 5 இருக்கைகள் தேவை
முதல் நபரை அமர வைக்க = 5 வழிகள்
2 வது நபரை அமர வைக்க = 4 வழிகள்
3 வது நபரை அமர வைக்க = 3 வழிகள்
4 வது நபரை அமர வைக்க = 2 வழிகள்
5 வது நபரை அமர வைக்க = 1 வழி
∴ 5 நபர்களையும் அமரவைக்க = 5 × 4 × 3 × 2 × 1 பெருக்கலின் அடிப்படைக்கொள்கையின்படி = 120 வழிகள் கிடைக்கும்
கேள்வி 2.
(i) ஒரு அலைபேசியில் 6 வெவ்வேறான இலக்கங்களைக் கொண்ட கடவுச் சொல் உள்ளது. அந்த கடவுச்சொல்லை மீட்டெடுக்க அதிக பட்சம் எத்தனை முயற்சிகளை செய்ய வேண்டும்?
தீர்வு:
-கடவுச்சொல்லில் உள்ள இலக்கங்களின் எண்ணிக்கை 6
∴ முதல் எண்ணை மீட்டெடுக்க = 10 வழிகள்
2ம் எண்ணை மீட்டெக்க = 9 வழிகள்
3ம் எண்ணை மீட்டெக்க = 8 வழிகள்
4ம் எண்ணை மீட்டெக்க = 7 வழிகள்
5ம் எண்ணை மீட்டெக்க = 6 வழிகள்
6ம் எண்ணை மீட்டெக்க = 5 வழிகள்
∴ கடவுச்சொல்லை மீட்டெடுக்க அதிகபட்சமான முயற்சிகள் = 10 × 9 × 8 × 7 × 6 × 5 = 151200 முயற்சிகள் செய்யலாம்
![]()
(ii) 4 வெவ்வேறு நிற கொடிகளில் 3 கொடிகளை ஒன்றின் கீழ் ஒன்றாக அமைத்து எத்தனை வெவ்வேறு விதமான சமிக்கைகளை 1] உருவாக்கலாம்?
தீர்வு:
மொத்த சமிக்கைகள் எண்ணிக்கை
வெவ்வேறு நிற கொடிகள் = 4
பயன்படுத்த வேண்டிய நிறங்கள் = 3
∴ முதல் இடம் = 4 வழிகள்
இரண்டாம் இடம் = 3 வழிகள்
மூன்றாம் இடம் = 2 வழிகள்
∴ பெருக்கலின் அடிப்படைக்கொள்கையின்படி, உருவாக்க வேண்டிய சமிக்கைகள் = 4 × 3 × 2 = 24 வழிகளில் சமிக்கைகளை உருவாக்கலாம்.
கேள்வி 3.
நான்கு குழந்தைகள் ஒரு ஓட்டப்பந்தயத்தில் ஓடுகிறார்கள்.
(i) முதல் இரண்டு இடங்களை எத்தனை வழிகளில் நிரப்பலாம்?
தீர்வு:
முதல் இடத்தை = 4 வழிகளிலும்
2 ம் இடத்தை = 3 வழிகளிலும் ஆக மொத்தம் பெருக்கலின் அடிப்படைக் கொள்கையின்படி = 4 × 3 = 12 வழிகளில் நிரப்பலாம்
(ii) அந்தபந்தயத்தை எத்தனை வழிகளில் முடிக்கலாம்?
தீர்வு:
∴ அந்த பந்தயத்தை = 4 × 3 × 2 × 1 வழிகளில்
= 4! = 24 வழிகளில் முடிக்கலாம்
![]()
கேள்வி 4.
2, 4, 6, 8 என்ற இலக்கங்களைப் பயன்படுத்தி எத்தனை 3 – இலக்க எண்களை
(i) இலக்கங்கள் திரும்ப வருமாறு
தீர்வு:
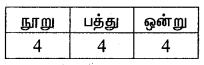
இலக்கங்கள் திரும்ப வருமாறு எனில் நிரப்பினால் = 4 × 4 × 4 = 64 வழிகளில் உருவாக்கலாம்
(ii) இலக்கங்கள் திரும்ப வராதவாறு காணலாம்.
தீர்வு:
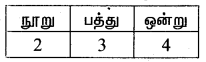
இலக்கங்கள் திரும்ப வராதவாறு எனில் = 4 × 3 × 2 = 24 வழிகளில் உருவாக்கலாம்
கேள்வி 5.
எத்தனை மூன்று – இலக்க எண்களை 3 ஆனது ஒன்றாம் இலக்க இடத்தில் வருமாறு
(i) இலக்கங்கள் திரும்ப வரும் நிலையில்
(ii) இலக்கங்கள் திரும்ப வராதவாறு காணலாம்.
தீர்வு:

இலக்கங்கள் திரும்ப வரும் வழியில்
ஒன்றாம் இடம் = 1
பத்தாம் இடம் = 10
நூறாம் இடம் = 9 (0 வைத் தவிர )
பெருக்கலின் அடிப்படைக்கொள்கையின்படி 3 ஆனது ஒன்றாம் இலக்க இடத்தில் திரும்ப வரும் நிலைகள் = 1 × 10 × 9 = 90
(ii) இலக்கங்கள் திரும்ப வராதவாறு

ஒன்றாம் இடம் = 1 வழியில்
பத்தாம் இடம் = 8 வழிகளில்
நூறாம் இடம் = 8 வழிகளில்
1, 2, 3, 4, 5, 6, 7, 8, (0 மற்றும் 9 ஐத் தவிர)
∴ மொத்த வழிகள் = 1 × 8 × 8 = 64
![]()
கேள்வி 6.
100 மற்றும் 500- க்கு இடையில் 0, 1, 2, 3, 4, 5 என்ற இலக்கங்களை பயன்படுத்தி
(i) இலக்கங்கள் திரும்ப வரும் நிலையில் எத்தனை எண்களை உருவாக்கலாம்.
(ii) இலக்கங்கள் திரும்ப வராமல் எத்தனை எண்களை உருவாக்கலாம்.
தீர்வு:
(i) இலக்கங்கள் திரும்ப வரும் நிலையில்

0, 1, 2, 3, 4, 5 என்ற இலக்கங்களில்
1-ம் இடத்தில் = 6 வழிகளில்
(6 இலக்கங்களைக்கொண்டு )
10-ம் இடத்தில் = 6 வழிகளில்
(6 இலக்கங்களைக்கொண்டு)
100ம் இடத்தில் = 4 வழிகளில்
(1, 2, 3, 4) ஐப் பயன்டுத்தி
∴ பெருக்கலின் அடிப்படைக்கொள்கையைப் பயன்படுத்தி கிடைக்கும் 3இலக்க எண்களின் எண்ணிக்கை = 4 × 6 × 6 = 144
(ii) இலக்கங்கள் திரும்ப வராமல் [Govt. MQP – 2018]
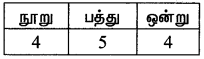
100 ம் இடம் = 4 வழிகளில்
10ம் இடம் = 5 வழிகளில்
1ம் இடம் = 4 வழிகளில்
∴ பெருக்கலின் அடிப்படைக் கொள்கையைப் பயன்படுத்தி
= 4 × 5 × 4
= 80 வழிகளில் பெறலாம்.
கேள்வி 7.
எத்தனை 3-இலக்க ஒற்றைப் படை எண்களை 0, 1, 2, 3,4, 5 என்ற இலக்கங்களை பயன்படுத்தி
(i) இலக்கங்கள் திரும்ப வராமல்
தீர்வு:
இலக்கங்கள் திரும்ப வராமல் (0, 1, 2, 3, 4, 5)

ஒற்றைப்பட எண்களை பயன்படுத்த
ஒன்றாம் இடம் = 3 வழிகளில் (1,3,5)
பத்தாம் இடம் = 4 வழிகளில்
நூறாம் இடம் = 4
(0, ஒன்றாம் இட இலக்கம் தவிர )
பெருக்கலின் அடிப்படைக் கொள்கையின் படி
= 3 × 4 × 4
= 48 வழிகளில் ஒற்றை எண்களை அமைக்கலாம்.
(ii) இலக்கங்கள் திரும்ப வருமாறு காணலாம்.
தீர்வு:
இலக்கங்கள் திரும்ப வருமாறு (0, 1, 2, 3, 4, 5)
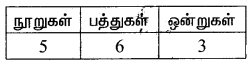
1ம் இடத்தை நிரப்புவதற்கு தேவையான வழிகள் = 3
10ம் இடத்தை நிரப்புவதற்கு தேவையான வழிகள் = 6
100ம் இடத்தை நிரப்புவதற்கு தேவையான வழிகள் = 5
∴ பெருக்கலின் அடிப்படைக்கொள்கையின்படி
= 3 × 6 × 5 = 90 வழிகள்
![]()
கேள்வி 8.
கீழ்க்காணும் நிபந்தனைக்கு உட்பட்டு 999 மற்றும் 10000-க்கு இடையே உள்ள எண்களை எண்ணுக.
(i) எந்த நிபந்தனையும் இல்லாமல்
தீர்வு:
எந்த நிபந்தனையும் இல்லாமல்
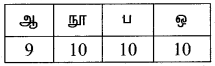
இலக்கங்கள் = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
1ம் இடம் = 10 வழிகள்
10ம் இடம் = 10 வழிகள்
100ம் இடம் = 10 வழிகள்
1000ம் இடம் = 9 வழிகள் (0-வைத்தவிர )
ஃமொத்த எண்கள் = 9 × 10 × 10 × 10 = 9000
(ii) எந்த இலக்கமும் திரும்ப வராமல்
தீர்வு:
எந்த இலக்கமும் திரும்ப வராமல்
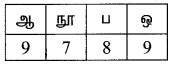
1000ம் இடம் = 9 வழிகளில்
1ம் இடம் = 9 வழிகளில்
10ம் இடம் = 8 வழிகளில்
100ம் இடம் = 7 வழிகளில்
பெருக்கலின் அடிப்படைக்கொள்கையின்படி = 9 × 7 × 8 × 9 = 4536
(iii) குறைந்தபட்சம் ஏதேனும் ஒரு இலக்கம் திரும்ப வருமாறு.
தீர்வு:
குறைந்தபட்சம் ஏதேனும் ஒரு இலக்கம் திரும்ப வருமாறு
தேவையான எண்ணிக்கை = மொத்த 4 இலக்க எண்கள் – எண்கள் திரும்ப வராமல் இருக்கும்போது உள்ள எண்களின் எண்ணிக்கை
= 9000 – 4536 = 4464.
கேள்வி 9.
0, 1, 2, 3, 4, 5 என்ற இலக்கங்களை பயன்படுத்தி, 5ஆல் வகுபடும், மூன்று – இலக்க எண்கள் கீழ்க்காணும் நிபந்தனைக்குட்பட்டு எத்தனை உள்ளன.
(i) இலக்கங்கள் திரும்ப வராமல்?
தீர்வு:
இலக்கங்கள் திரும்ப வராமல்
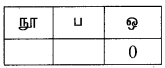
1 ஆம் இடத்தில் 0 என்க.
10 மற்றும் 100 – வது இடத்தில் முறையே 4 மற்றும் 5 இலக்கங்கள்
வழிகளின் எண்ணிக்கை = 4 × 5 × 1 = 20
(ii) இலக்கங்கள் திரும்ப வருமாறு?
தீர்வு:
1ஆம் இடத்தில் 5 என்க.
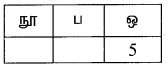
நூறாவது இடத்தை , நிரப்ப தேவையான இலக்கங்கள் 1, 2, 3, 4 (0 வைத் தவிர) = 4 வழிகள் மேலும் பத்தாவது இடத்தை நிரப்ப 4 இலக்கங்கள் (0 வைத் தவிர)
∴ வழிகளின் எண்ணிக்கை = 4 × 4 = 16
∴ மொத்த வழிகளின் எண்ணிக்கை = 20 + 16 × 36
![]()
கேள்வி 10.
A என்ற இடத்திலிருந்து B என்ற இடத்திற்கு செல்ல B1, B2 என்ற இரண்டு பேருந்து வழித்தடங்களும் T1, T2 என்ற இரண்டு இரயில் வழித்தடங்களும் மேலும் A1 என்ற வான் வழித்தடமும் உள்ளது. B என்ற இடத்திலிருந்து C என்ற இடத்திற்கு செல்ல B’, என்ற ஒரு பேருந்து வழித்தடமும், T’1, T’2 என்ற இரண்டு இரயில் வழித்தடங்களும் மேலும் A’1 என்ற வான் வழித்தடமும் உள்ளது. A என்ற இடத்திலிருந்து C என்ற இடத்திற்கு B என்ற இடம் வழியே ஒரே வழித்தடத்தை மீண்டும் பயன்படுத்தாமல் எத்தனை வழிகளில் செல்லலாம்?
தீர்வு:
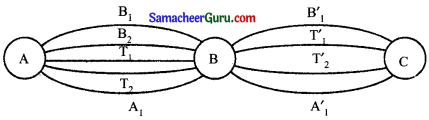
Aலிருந்து Cக்கு ஒரே வழித்தடத்தை மீண்டும் பயன்படுத்தாமல் கீழ்க்கண்ட வழிகளில் செல்லலாம். (B1, T’1) (B1, T’2) (B1, A1) (B2, T’1) (B2, T’2) (B2, A’1) (T1, B’1) (T1, A’1) (T2, B’1) (T2, A’1) (A1,B’1) (A1, T’1) மற்றும் (A1, T’2).
தேவையான வழித்தடங்களின் எண்ணிக்கை = 13.
கேள்வி 11.
1-க்கும் 1000-க்கும் இடையே உள்ள (இரண்டையும் ! உள்ளடக்கிய) எண்களில் 2 ஆலும் 5 ஆலும் வகுபடாத எண்களின் எண்ணிக்கையைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட எண்க ள் 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
ஒரு எண் 2 மற்றும் 5 ஆல் வகுபடாமல் இருக்க வேண்டுமானால் அந்த எண் 1, 3, 7, 9 ல் முடிந்திருக்க வேண்டும்,
தேவையான ஓரிலக்க எண்கள் = 4 …… (1)
இரண்டு இலக்க எண்கள்
| பத்துகள் | ஒன்றுகள் |
| 9 | 4 |
1ம் இடத்தில் = 4 வழிகளில் (1, 3, 7, 9 ல் இருக்க)
10ம் இடத்தில் = 9 வழிகளில்
∴ தேவையான ஈரிலக்க எண்கள் = 4 × 9 = 36 …..(2)
மூன்று இலக்க எண்கள்

1ம் இடம் = 4 வழிகளில்
(1,3,7,9 ல் இருக்க )
10ம் இடத்தில் = 10 வழிகளில்
100ம் இடம் = 9 வழிகளில்
∴ தேவையான மூன்றிலக்க எண் = 4 × 9 × 10 = 360 ….. (3)
4 இலக்க எண் 1000. அது 2, 5 ஆல் வகுபடும்
∴ தேவையான எண்கள் (கூட்டலின் அடிப்படைக் கொள்கையின்படி)
4 + 36 + 360 மற்றும் ((1) (2) மற்றும் (3))
![]()
கேள்வி 12.
LOTUS எனும் வார்த்தையிலுள்ள எழுத்துகளைப் பயன்படுத்தி
(i) L இல் ஆரம்பித்து அல்லது S இல் முடிக்கும் வகையில் எத்தனை எழுத்துச் சரங்கள் உள்ளன.
தீர்வு:
L ல் ஆரம்பித்து அல்லது S ல் முடிக்கும் வகையில் உள்ள எழுத்துச் சரங்கள்
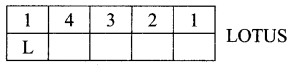
டல் ஆரம்பிக்குமாறு அமைவன
= 1 × 4 × 3 × 2 × 1 = 24 …… (1)
Sல் முடியுமாறு அமைவன
= 1 × 4 × 3 × 2 × 1 = 24 ……. (2)
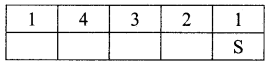
L லில் ஆரம்பித்தும் S ல் முடியுமாறும் எழுத்துச்சரங்கள் = 3 × 2 × 1 = 6 …..(3)
∴ கூட்டலின் அடிப்படைக் கொள்கையின்படி டல் ஆரம்பித்தோ அல்லது Sல் முடியுமாறு அமைவன
= 24 + 24 – 6 = 48 – 6 = 42
(ii) L இல் துவங்கவோ, மற்றும் S இல்
முடிக்கவோ கூடாத எழுத்துச் சரங்களின் எண்ணிக்கையைக் காண்க.
தீர்வு:
L லில் ஆரம்பிக்கவோ S-ல் முடியவோ கூடாத எழுத்துச்சரங்களின் எண்ணிக்கை
LOTUS என்ற வார்த்தையில் உள்ள எழுத்துக்களிலிருந்து உருவாக்கப்படும் மொத்த எழுத்துச் சரங்கள்
= 5 × 4 × 3 × 2 × 1 = 120
டல் ஆரம்பித்தோ அல்லது Sல் முடிந்தோ இருக்கக்கூடாத எழுத்துச் சரங்கள் = மொத்த எண்ணிக்கை L, Sல் தொடக்க முடிவு எழுத்தாக இல்லாத எழுத்துச் சரங்களின் எண்ணிக்கை = 120 – 42 = 78
கேள்வி 13.
(i) ஒவ்வொரு குறிக்கோள் வினாவிற்கும் 4 வாய்ப்புகள் உள்ளன. 6 வினாக்களுக்கு எத்தனை வழிகளில் விடையளிக்கலாம்?
(ii) 3 புறாகூடுகளில் 10 புறாக்களை எத்தனை வழிகளில் தங்க வைக்கலாம்?
(iii) 10மாணவர்களுக்கு 12வெவ்வேறான பரிசுகளை எத்தனை வழிகளில் பகிர்ந்தளிக்கலாம்?
தீர்வு:
(i) ஒவ்வொரு குறிக்கோள் வினாவிற்கும் உள்ள வாய்ப்புகள் = 4
மொத்த வினாக்கள் = 6
∴ மொத்த வாய்ப்புகள் = 4 × 4 × 4 × 4 × 4 × 4 = 46
(ii) புறாக்கூடுகள் = 3
புறாக்கள் = 10
∴ 3 புறாக்கூடுகளில் 10 புறாக்களை தங்க வைக்கும் வழிகள் = 310
(iii) ஒவ்வொருமுதல்பரிசும் எந்த ஒருமாணவர்களுக்கும் 10 வழிகளில் பகிர்ந்த ளிக்கலாம்
∴ 12 வெவ்வேறான பரிசுகளை ஒவ்வொரு 10 மாணவர்களுக்கும்
= 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10
= 1012 வழிகளில் பகிர்ந்த ளிக்கலாம்.
![]()
கேள்வி 14.
மதிப்பினைக் காண்க.
(i) 6!
தீர்வு:
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
(ii) 4! + 5!
தீர்வு:
4! + 5! = 4 × 3 × 2 × 1 + 5 × 4 × 3 × 2 × 1
= 24 + 120 = 144.
(iii) 3! – 2!
தீர்வு:
3! – 2! = 3 × 2 × 1 – 2 × 1 = 6 – 2 = 4
(iv) 3! × 4!
தீர்வு:
3! × 4! = (3 × 2 × 1) × (4 × 3 × 2 × 1)
= 6 × 24 = 144.
(v) \(\frac{12 !}{9 ! \times 3 !}\)
தீர்வு:
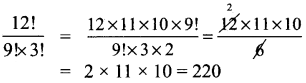
(vi) \(\frac{(n+3) !}{(n+1) !}\)
தீர்வு:
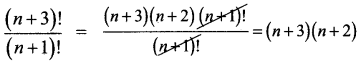
கேள்வி 15.
மதிப்புக் காண்க \(\frac{n !}{r !(n-r) !}\), இங்கு
(i) n = 6, r = 2
தீர்வு:
n = 6, r = 2 என கொடுக்கப்பட்டுள்ளது.
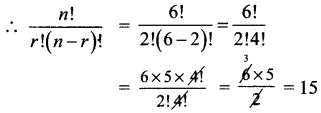
(ii) n = 10, r = 3.
தீர்வு:
கொடுக்கப்பட்டுள்ளது n = 10, r = 3
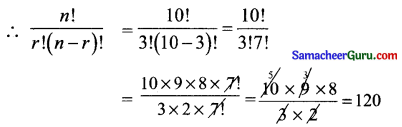
(iii) எந்த 7-க்கும், r = 2.
தீர்வு:
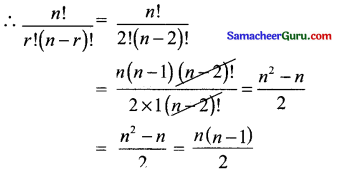
![]()
கேள்வி 16.
n-ன் மதிப்பை காணக
(i) (n + 1)! = 20 (n – 1)!
தீர்வு:
(i) (n + 1)! = 20 (n – 1)! கொடுக்கப்பட்டுள்ளது
![]()
⇒ (n + 1) (n) = 20
⇒ n2 + n – 20 = 0
⇒ (n + 5) (n – 4) = 0
n = -5 ஆக இருக்க முடியாது
∴ n = 4
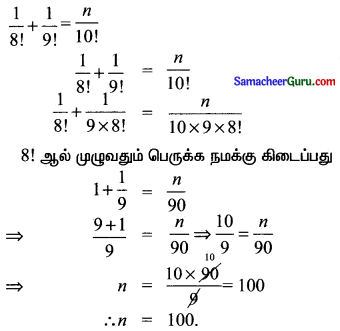
(ii) \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{n}{10 !}\)
தீர்வு: