Samacheer Kalvi 11th Maths Guide Chapter 4 சேர்ப்பியல் மற்றும் கணிதத் தொகுத்தறிதல் Ex 4.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 சேர்ப்பியல் மற்றும் கணிதத் தொகுத்தறிதல் Ex 4.5 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 4 சேர்ப்பியல் மற்றும் கணிதத் தொகுத்தறிதல் Ex 4.5

சரியான அல்லது மிகவும் ஏற்புடைய விடையினைத் தேர்ந்தெடுக்கவும்

கேள்வி 1.
2, 4, 5, 7 ஆகிய அனைத்து எண்களையும் பயன்படுத்தி உருவாக்கப்படும் நான்கு இலக்க எண்களில் 10-ஆவது இடத்திலுள்ள அனைத்து எண்களின் கூடுதல் .
(1) 432
(2) 108
(3) 36
(4) 18
குறிப்பு:

(திரும்ப வராமல்) உருவாக்கப்படும் எண்களின் எண்ணிக்கை = 4 × 3 × 2 × 1 = 24
2s, 4s, 5s, 7s க்கள் ஒன்றாம் இடம், பத்தாம் இடம், மற்றும் பிறவற்றிலும் வரும்.
இந்த எண்களின் மொத்தம் (3 + 4 + 5 + 6)
∴ ஒவ்வொன்றும் ஆறு முறை பத்தாம் இடத்தில்.
∴ பத்தாம் இடத்தில் உள்ள எண்களின் கூடுதல்
= 6(2 + 4 +5+7) = 108
விடை:
(2) 108

கேள்வி 2.
ஒரு தேர்வில் 5 வாய்ப்புகளையுடைய மூன்று பல்வாய்ப்பு வினாக்கள் உள்ளன. ஒரு மாணவன் எல்லா வினாக்களுக்கும் சரியாக விடையளிக்கத் தவறிய வழிகளின் எண்ணிக்கை
(1) 125
(2) 124
(3) 64
(4) 63
குறிப்பு:
பதிலளிக்கும் வழிகளின் எண்ணிக்கை = 5³ = 125
சரியான விடை = 1
∴ தவறான விடைகளின் எண்ணிக்கை = 125 – 1
= 124
விடை:
(2) 124

கேள்வி 3.
30 மாணவர்களைக் கொண்ட வகுப்பில் கணிதத்தில் முதலாவது மற்றும் இரண்டாவது, இயற்பியலில் முதலாவது மற்றும் இரண்டாவது, வேதியியலில் முதலாவது மற்றும் ஆங்கிலத்தில் முதலாவது என பரிசுகளை வழங்கும் மொத்த வழிகளின் எண்ணிக்கை
(1) 30⁴ × 29²
(2) 30³ × 29³
(3) 30² × 29⁴
(4) 30 × 29⁵
குறிப்பு:
கணிதத்தில் முதல் ⇒ 30 வழிகள். கணிதத்தில் இரண்டாவது 29 வழிகள் அதை போல பிற பாடங்களுக்கும் 30 × 29 × 30 × 29 × 30 × 30
= 30⁴ × 29²
விடை:
(1) 30⁴ × 29²

கேள்வி 4.
எல்லாம் ஒற்றை எண்களாகக் கொண்ட 5 இலக்க எண்களின் எண்ணிக்கை
(1) 25
(2) 5⁵
(3) 5⁶
(4) 625
குறிப்பு:

ஒற்றை எண்கள் 1, 3, 5, 7, 9
∴ எல்லாம் ஒற்றை எண்களாக கொண்ட 5 இலக்க எண்களின் எண்ணிக்கை
= 5 × 5 × 5 × 5 × 5 = 5⁵
விடை:
(2) 5⁵

கேள்வி 5.
3 விரல்களில், 4 மோதிரங்களை அணியும் வழிகளின் எண்ணிக்கை
(1) 4³ – 1
(2) 3⁴
(3) 68
(4) 64
குறிப்பு:
4 மோதிரங்களை 3 விரல்களில் 3⁴ வழிகளில் அணியலாம்.
விடை:
(2) 3⁴

கேள்வி 6.
^{(n + 5)}P_{n + 1} = \(\left(\frac{11(n-1)}{2}\right)\) ^{(n + 3)}P_n. எனில் n-ன் மதிப்பு
(1) 7 மற்றும் 11
(2) 6 மற்றும் 7
(3) 2 மற்றும் 11
(4) 2 மற்றும் 6.
குறிப்பு:

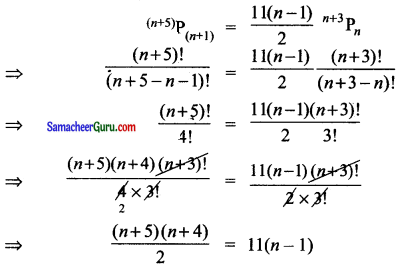
⇒ (n² + 9n + 20) = (11n – 11) × 2
⇒ n² + 9n + 20 = 22n – 22
⇒ n² – 13n + 42 = 0
⇒ (n – 6) (n – 7) = 0 ⇒ n = 6 (அல்ல து) 7
விடை:
(2) 6 மற்றும் 7

கேள்வி 7.
அடுத்தடுத்தாமிகை முழு எண்களின் பெருக்கற்பலன் எதனால் வகுபடும்.
(1) r!
(2) (r – 1)!
(3) (r + 1)!
(4) r^r.
குறிப்பு:
அடுத்தடுத்த r மிகை முழுக்கள் r! (தேற்றம்)
விடை:
(1) r!

கேள்வி 8.
குறைந்தபட்சம் ஒரு இலக்கம் மீண்டும் வருமாறு 5 இலக்க தொலைபேசி எண்களின் எண்ணிக்கை.
(1) 90000
(2) 10000
(3) 30240
(4) 69760.
குறிப்பு:
நிலை (i) : பூஜ்ஜியம் முதலிடத்தில் அனுமதிக்கப் பட்டால்: 0,1, 2, …… 9 என்ற இலக்கங்களை உபயோகித்து உருவாக்கப்பட்டு 5 இலக்க தொலைபேசி எண்களின் எண்ணிக்கை 10. எந்த இலக்கமும் திரும்பவும் வராத 5 இலக்க தொலைபேசி எண்களின் எண்ணிக்கை ¹⁰P₅ = 30240

நிலை(ii) : பூஜ்ஜியம் முதலிடத்தில் அனுமதிக்கப் படாவிட்டால்:

திரும்ப வரும் இலக்கங்களையும் கொண்ட எண்களின் எண்ணிக்கை 9 × 10 × 10 × 10 × 10 = 90000 (முதல் இலக்கம் பூச்சியமாக இருக்காது ஏனெனில் எந்த தொலைபேசி எண்ணும் பூச்சியத்தில் துவங்குவதில்லை)
இலக்கங்கள் திரும்பவும் வராத எண்களின் எண்ணிக்கை 9 × 9 × 8 × 7 × 6 = 37216
∴ குறைந்தது ஒரு இலக்கமாவது திரும்பவும் வரக்கூடிய எண்க ளின் எண்ணிக்கை 90000 – 37216 = 52,784
விடை:
(4) 69760 (or) 52,784

கேள்வி 9.
^{a2 – a}C₂ = ^{a2 – a}C₄ எனில் a – ன் மதிப்பு
(1) 2
(2) 3
(3) 4
(4) 5
குறிப்பு:
^{a2 – a}C₂ = ^{a2 – a}C₄ ⇒ ^{a2 – a}C₄ ⇒ a² – a – 4 = 2
⇒ a² – a – 6 = 0 ⇒ (a – 3) (a + 2) = 0
⇒ a = 3 (அல்லது) -2
விடை:
(2) 3

கேள்வி 10.
ஒரு தளத்தில் 10 புள்ளிகள் உள்ளன. அவற்றில் 4 ஒரே கோடமைவன. ஏதேனும் இரு புள்ளிகளை இணைத்து கிடைக்கும் கோடுகளின் எண்ணிக்கை.
(1) 45
(2) 40
(3) 39
(4) 38.
குறிப்பு:
கோடுகளின் எண்ணிக்கை
= ¹⁰C₂ – ⁴C₂ + 1 = 45 – 6 + 1 = 4
விடை:
(2) 40

கேள்வி 11.
ஒரு விழாவிற்கு 12 நபர்களில் 8 நபர்களை ஒரு பெண் அழைக்கிறார். இதில் இருவர் ஒன்றாக விழாவிற்கு வரமாட்டார்கள் எனில், அவர்களை அழைக்கும் வழிகளின் எண்ணிக்கை.
(1) 2 × ¹¹C₇ + ¹⁰C₈
(2) ¹¹C₇ + ¹⁰C₈
(3) ¹²C₈ – ¹⁰C₆
(4) ¹⁰C₆ + 2!.
குறிப்பு:
12 நபர்களில் 8 நபர்களை தேர்ந்தெடுக்கும் வழிகள்
¹²C₈. A மற்றும் B விழாவிற்கு வருகிறார்கள் என்க. மீதமுள்ள 10 பேரில் 6 பேர் ¹⁰C₆ வழிகளின் தேர்ந்தெடுக்கலாம்.
∴ இருவரும் ஒன்றாக விழாவிற்கு வராமல் இருப்பதற்கான வழிகள் ¹²C₈ – ¹⁰C₆
விடை:
(3) ¹²C₈ – ¹⁰C₆

கேள்வி 12.
நான்கு இணையான கோடுகளின் தொகுப்பானது மூன்று இணையான கோடுகளைக் கொண்ட மற்றொரு தொகுப்பை வெட்டும்போது உருவாகும் இணைகரங்களின் எண்ணிக்கை.
(1) 6
(2) 9
(3) 12
(4) 18
குறிப்பு:
இணைகரங்களின் எண்ணிக்கை = ⁴C₂ × ³C₂
⇒ 6 × 3 = 18
விடை:
(4) 18

கேள்வி 13.
ஓர் அறையில் உள்ள ஒவ்வொருவரும் மற்றவருடன் கைக்குலுக்கிறார்கள். 66 கைக்குலுக்கல் நிகழ்கின்றது எனில், அந்த அறையில் உள்ள நபர்களின் எண்ணிக்கை
(1) 11
(2) 12
(3) 10
(4) 6
குறிப்பு:
கைக்குலுக்கல்களின் எண்ணிக்கை = 66
n நபர்கள் உள்ளார்கள் என்க.
கைக்குலுக்கல்களின் எண்ணிக்கை
= (n – 1) + (n – 2) + ….. + 2 + 1
= \(\frac{(n-1) n}{2}\) = 66 ⇒ n² – n = 132 ⇒ n² – n – 132 = 0
⇒ (n – 12) (n + 11) = 0 ⇒ n = 12 (அல்லது) – 11 (சாத்தியமில்லை )
விடை:
(2) 12

கேள்வி 14.
44 மூலைவிட்டங்கள் உள்ள ஒரு பலகோணத்தின் பக்கங்களின் எண்ணிக்கை
(1) 4
(2) 4!
(3) 11
(4) 22
குறிப்பு:
மூலைவிட்டங்களின் எண்ணிக்கை
= ⁿC₂ – n ⇒ \(\frac{(n-1) n}{2}\) – n = 44 = n² – n- 2n
= 88 ⇒ n² – 3n – 88 = 0 ⇒ (n – 11) (n + 8) = 0
⇒ n = 11 (அல்லது) n = -8
விடை:
(3) 11

கேள்வி 15.
எந்த இரண்டு கோடுகளும் இணையாக இல்லாமலும் மற்றும் எந்த மூன்று கோடுகளும் ஒரு புள்ளியில் வெட்டிக் கொள்ளாமலும் இருக்குமாறு ஒரு தளத்தின் மீது 10 நேர்க்கோடுகள் வரையப்பட்டால், கோடுகள் வெட்டிக் கொள்ளும் புள்ளிகளின் மொத்த எண்ணிக்கை. .
(1) 45
(2) 40
(3) 10!
(4) 210
குறிப்பு:
வெட்டிக் கொள்ளும் புள்ளிகளின் எண்ணிக்கை

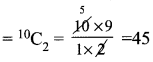
விடை:
(1) 451

கேள்வி 16.
ஒரு தளத்தில் உள்ள 10 புள்ளிகளில் 4 புள்ளிகள் ஒரு கோடமைவன எனில், அவற்றைகொண்டு உருவாக்கும் முக்கோணங்களின் எண்ணிக்கை
(1) 110
(2) ¹⁰C₃
(3) 120
(4) 116
குறிப்பு:
முக்கோணங்களின் எண்ணிக்கை = ¹⁰C₃ – ⁴C₃

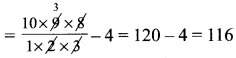
விடை:
(4) 116

கேள்வி 17.
²ⁿC₃ : ⁿC₃ = 11 : 1 n-ன் மதிப்பு
(1) 5
(2) 6
(3) 11
(4) 7
குறிப்பு:

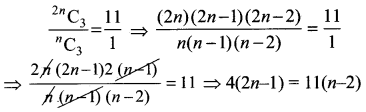
8n – 4 = 11n – 22 ⇒ 18 = 3n ⇒ n = 6
விடை:
(2) 6

கேள்வி 18.
^{(n – 1)}C_r + ^{(n – 1)}C_{(r – 1)} என்ப து
(1) ^{(n + 1)}C_r
(2) ^{(n – 1)}C_r
(3) ⁿC_r
(4) ⁿC_{r – 1}
குறிப்பு:
^{(n – 1)}C_r + ^{(n – 1)}C_{(r – 1)} = ⁿC_r
விடை:
(3) ⁿC_r

கேள்வி 19.
52 சீட்டுகள் உள்ள ஒரு சீட்டுக்கட்டிலிருந்து தேர்ந்தெடுக்கப்படும் 5 சீட்டுகளில் குறைந்தபட்சம் ஒரு இராஜா சீட்டு இருக்குமாறு உள்ள வழிகளின் எண்ணிக்கை
(1) ⁵²C₅
(2) ⁴⁸C₅
(3) ⁵²C₅ + ⁴⁸C₅
(4) ⁵²C₅ – ⁴⁸C₅
குறிப்பு:
⁵²C₅ எல்லா இயலக்கூடியவைகளும்
கொண்டிருக்கும் (அரசன் இல்லை, 1 அரசன், 2 அரசர்கள், 3 அரசர்கள், 4 அரசர்கள்) 48C, இல் அரசர்கள் ஏதுமில்லை தேவையான வழிகள் ⁵²C₅ – ⁴⁸C₅
விடை:
(4) ⁵²C₅ – ⁴⁸C₅

கேள்வி 20.
ஒரு சதுரங்க அட்டையில் உள்ள செவ்வகங்களின் எண்ணிக்கை.
(1) 81
(2) 99
(3) 1296
(4) 6561
குறிப்பு:
சதுரங்க அட்டையில் உள்ள செவ்வகங்களின் எண்ணிக்கை

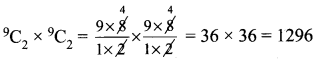
விடை:
(3) 1296

கேள்வி 21.
2 மற்றும் 3 என்ற இலக்கங்களை கொண்டு உருவாக்கப்படும் 10 இலக்க எண்களின் எண்ணிக்கை
(1) ¹⁰C₂ + ⁹C₂
(2) 2¹⁰
(3) 2¹⁰ – 2
(4) 10!
குறிப்பு:
2 மற்றும் 3 என்ற இலக்கங்களை கொண்டு உருவாக்கப்படும் 10 இலக்க எண்களின் எண்ணிக்கை 2¹⁰.
விடை:
(2) 2¹⁰

கேள்வி 22.
P. என்பது P, ஐ குறித்தால் 1 + P₁ + 2P₂ + 3P₃ + …… + nP_n என்ற தொடரின் கூடுதல்
(1) P_n+1
(2) P_n+1 – 1
(3) P_n-1 + 1
(4) ⁿ⁺¹P_n+1
குறிப்பு:

⇒ நிரூபணம் n = 1 என்க,
LHS = 1 + 1 = 2; RHS = \(\lfloor 2\) = 2
n = 1 க்கு சரி, n = 0 க்கும் கூட இது சரி, n = k க்கு சரி என்க.

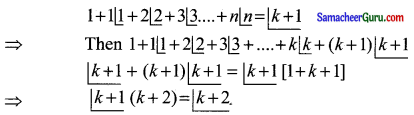
விடை:
(2) P_n+1 – 1

கேள்வி 23.
முதல் 1 ஒற்றை இயல் எண்களின் பெருக்கலின் மதிப்பு
(1) ²ⁿC_n × ⁿP_n
(2) \(\left(\frac{1}{2}\right)^{n}\) × ²ⁿC_n × ⁿP_n
(3) \(\left(\frac{1}{4}\right)^{n}\) × ²ⁿC_n × ⁿP_n
(4) ⁿC_n × ⁿP_n
குறிப்பு:

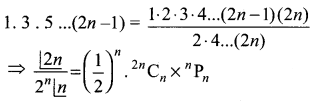
விடை:
(2) \(\left(\frac{1}{2}\right)^{n}\) × ²ⁿC_n × ⁿP_n

கேள்வி 24.
ⁿC₄, ⁿC₅, ⁿC₆ ஆகியவை APயில் (கூட்டுத்தொடரில்)
உள்ள ன எனில், n-ன் மதிப்பு
(1) 14
(2) 11
(3) 9
(4) 5
குறிப்பு:
கொடுக்கப்பட்டுள்ள ⁿC₄, ⁿC₅, ⁿC₆ ஆகியவை AP யில் உள்ளன.


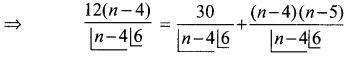
= 12n – 48 = 30 + n² – 9n + 20
⇒ n² – 21n + 98 = 0
(n – 14) (n- 7) = 0
⇒ n = 14 (அல்லது) n = 7.
விடை:
(1) 14

கேள்வி 25.
1 + 3 + 5 + 7 + …… + 17 -ன் மதிப்பு
(1) 101
(2) 81
(3) 71
(4) 61
குறிப்பு:
1 + 3 + 5 + 7 + ……. + 17 = 9² = 81
விடை:
(2) 81