Samacheer Kalvi 11th Maths Guide Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.1 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.1

கேள்வி 1.
விரிவுபடுத்து.
(i) \(\left(2 x^{2}-\frac{3}{x}\right)^{3}\)
தீர்வு:
\(\left(2 x^{2}-\frac{3}{x}\right)^{3}\)

(ii) (2x² – 3\(\sqrt{1-x^{2}}\))⁴ + (2x² + 3\(\sqrt{1-x^{2}}\))
தீர்வு:

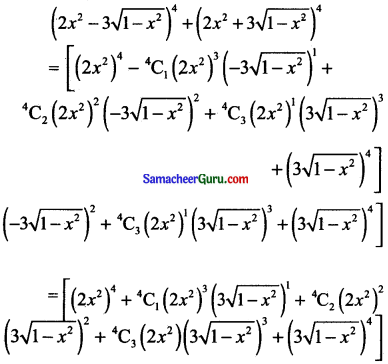
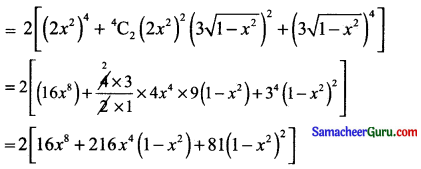
கேள்வி 2.
மதிப்புக் காண்க.
(i) 102⁴
(ii) 99⁴
(ill) 9⁷
தீர்வு:
(i) (a + b)ⁿ = ⁿC₀aⁿ b⁰ + ⁿC₁a^{n – 1} b¹ + ⁿC₂a^{n – 2} b² + ……………. + ⁿC_na⁰ bⁿ
⇒ (102)⁴ = (100 + 2)⁴ = (100)⁴ + ⁴C₁(100³)(2¹) + ⁴C₂(100²)(2² ) + ⁴C₃(100¹)(2³ ) + ⁴C₄(100⁰)(2⁴ )
= 100000000 + 2(1000000)(2) + \(\frac{4 \times(3)}{2(1)}\) (10000)(4)
= 100000000 + 8000000 + 240000 + 3200 + 16
= 108,243,216

(ii) ∵ (a – b)ⁿ = ⁿC₀aⁿ – ⁿC₁a^{n – 1} b + ⁿC₂a^{n – 2} b² + ……………. + ⁿC_na⁰ bⁿ
⇒ 99⁴ = (100 – 1)⁴
= 100⁴ – ⁴C₁100³ + ⁴C₂100² – ⁴C₃100(1³) + 1⁴

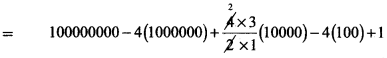
= 100000000 – 4000000 + 60000 – 400 + 1
= 96,059,601

(iii) ∵ (a – b)ⁿ = ⁿC₀aⁿ – ⁿC₁a^{n – 1} b + ⁿC₂a^{n – 2} b² + ……………. + ⁿC_nbⁿ
⇒ 9⁷ = (10 – 1)⁷ = 10⁷ – ⁷C₁10⁶ + ⁷C₂10⁵ – ⁷C₃10⁴ + ⁷C₄10³ – ⁷C₅10² + ⁷C₆10^-1


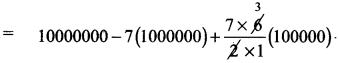
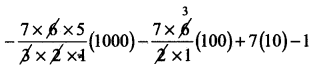
= 10000000 – 7000000 + 2100000 – 350000 + 35000 – 2100 + 70 – 1
= 4782969

கேள்வி 3.
ஈருறுப்புத் தேற்றத்தைப் பயன்படுத்தி (1.01)^1000000 மற்றும் 10000 ஆகியவற்றில் எது பெரியது எனக் காண்க.
தீர்வு:
(1.01)^1000000 – 10000
= (1 +.01)^1000000 10.000
= ¹⁰⁰⁰⁰⁰C₀ + ^1000000C₁ (.01) + ^1000000C₂(.01)² + ….
+ (.01)^1000000 – 10,000
= (1 + 1000000 × (.01) + சாதகமான எண்) – 10,000
= 1 + சாதகமான எண்
∴ (1.01)^1000000 – 10,000 > 0 ⇒ (1.01)^1000000 > 10,000.

கேள்வி 4.
\(\left(x^{2}+\frac{1}{x^{3}}\right)^{10}\) -ன் விரிவில் 15-ன் கெழுவைக் காண்க.
தீர்வு:
\(\left(x^{2}+\frac{1}{x^{3}}\right)^{10}\) ,n = 10, x = x², a = \(\frac{1}{x^{3}}\)
∴ பொது உறுப்பு T_{r + 1} = ⁿC_r x^n-r a^r
⇒ T_{r + 1} = ¹⁰C_r(x²)^{10 – r}\(\left(\frac{1}{x^{3}}\right)^{r}\)
= ¹⁰C_r x^{20 – 2r} x^-3r.
= ¹⁰C_r x^{20 – 5r} …(1)
x¹⁵ன் கெழுவினைக் காண,
20 – 5r = 15 என பிரதியிட
⇒ 20 – 15 = 5r
⇒ r = 1 என (1) ல் பிரதியிட
T₂ = ¹⁰C₁ x^{20 – 5} = 10 C₁ x¹⁵
x¹⁵ ன் கெழு 10.

கேள்வி 5.
\(\left(x^{2}-\frac{1}{x^{3}}\right)^{6}\) -ன் விரிவில் x⁶ மற்றும் x²-ன் கெழுக்களைக் காண்க.
தீர்வு:
\(\left(x^{2}-\frac{1}{x^{3}}\right)^{6}\), n = 6, x = x², a = \(\frac{-1}{x^{3}}\)
∴ பொது உறுப்பு ⇒ T_{r + 1} = ⁿC_r x^{n – r} a^r
⇒ T_{r + 1}= ⁶C_r(x²)^{6 – r}\(\left(\frac{-1}{x^{3}}\right)^{r}\)
= (-1)^{r 6}C_r x^{12 – 5r} ……. (1)
x⁶ ன் கெழுவினைக்கான 12 – 5r = 6 எனக்கொள்க
12 – 5r = 6 ⇒ 12 – 6 = 5r ⇒ 6 = 5r
r = \(\frac{6}{5}\)
இங்கு இருக்கமுடியாது
x² – உன் கெழுவைக் காண 12 – 5r = 2 என பிரதியிட
12 – 5r = 2
⇒ 12 – 2 = 5r ⇒ 10 = 5r ⇒ r = 2
r = 2 என (1) ல் பிரதியிட

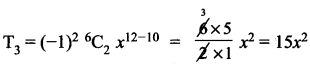
∴ x² சன்கெழு = 15.

கேள்வி 6.
(1 + x³)⁵⁵⁰ \(\left(x^{2}+\frac{1}{x}\right)^{5}\) -ன் விரிவில் x²-ன் கொழுமைக்
தீர்வு:


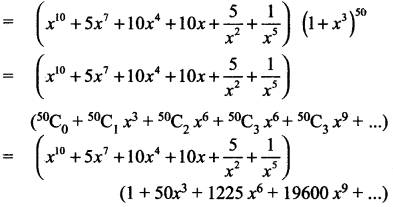
x⁴ -ன் கெழு
= 10 (மாறிலி உறுப்பு (1 + x³)⁵⁰) + 10 [(1 + ³)⁵⁰ ல் உள்ள x³ ன் கெழு + 5 (x⁶ ன் கெழு) + 1 (x⁹ ன்கெழு)
= 10(1) + 10(50) + 5(1225) + 1(19600)
(∵ (1)-ஐப் பயன்படுத்தி)
= 10 + 500 + 6125 + 19600 = 26235
∴ x⁴ -ன் கெழு = 26235.

கேள்வி 7.
\(\left(2 x^{3}-\frac{1}{3 x^{2}}\right)^{5}\) -ன் விரிவில் மாறிலி உறுப்பைக் காண்க.
தீர்வு:

கேள்வி 8.
3⁶⁰⁰-ன் கடைசி இரண்டு இலக்கங்களைக் காண்க.
தீர்வு:
3⁶⁰⁰ = (3²)³⁰⁰ = 9³⁰⁰ என்க .
⇒ 3⁶⁰⁰ = (10 – 1)³⁰⁰
ஈருறுப்புத் தேற்றத்தைப் பயன்படுத்தி
3⁶⁰⁰ = ³⁰⁰C₀ (10)^300_300C₁, (10)²⁹⁹ + ³⁰⁰C₂ 10²⁹⁸ + …. + 1)
= (10)³⁰⁰ – 300(10)²⁹⁹ + ….. – 300(10) + 1
∴ கடைசி இரு உறுப்புகள் 0, 1.

கேள்வி 9.
எல்லா மிகை முழு எண் 1-க்கும் 9ⁿ⁺¹ – 8n – 9 என்பது 64ஆல் வகுபடும் என ஈருறுப்புத தேற்றம் மூலம் நிறுவுக.
தீர்வு:

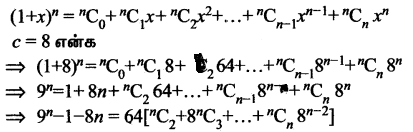
⇒ 9ⁿ – 8n – 1 ஆனது nன் அனைத்து மிகை முழுக்களும் 64 ஆல் வகுபடும்
∴ n = n + 1 என பிரதியிட
9^{n + 1} – 8(n + 1) – 1 ஆனது –ன் அனைத்து மிகை முழுக்களும் 64 ஆல் வகுபடும்
⇒ 9^{n + 1} – 8n – 8 – 1 ஆனது 64 ஆல் வகுபடும்.
⇒ 9^{n + 1} – 8n – 9 ஆனது 64 ஆல் வகுபடும்.

கேள்வி 10.
n ஒரு ஒற்றைப்படை மிகை முழு எண் எனில், (x + y)ⁿ – ன் விரிவில் மைய உறுப்புகளின் கெழுக்கள் சமம் என நிறுவுக.
தீர்வு:
(x + y)ⁿ கொடுக்கப்பட்டது. இதில் ) ஓர் ஒற்றை எண் எனில் (x + y)ⁿ

கேள்வி 11.
n ஒரு மிகை முழு எண் மற்றும் 7 என்பது குறையற்ற முழு எண் எனில், (1 + x)ⁿ-ன் விரிவில் மற்றும் x^{n – r} உறுப்புகளின் கெழுக்கள் சமம் என நிறுவுக.
தீர்வு:
(1 + x)ⁿ = n, x = 1, a = x
பொது உறுப்பு t_{r + 1} = ⁿC_r x^{n – r} d .
⇒ t_{r + 1} = ⁿC_r 1^{n – r} x^r = ⁿC_r x^r ….(1)
ⁿC_r -ல் x^r -ன் கெழுவைக்கான
r = n – r-என பிரதியிட
T_{n – r + 1} = ⁿC_{n – r} x^{n – r}
∴ x^rபன் கெழு மற்றும் x^{n – r} “-ன் கெழு உறுப்பின் கெழு ⁿC_{n – r} சமமாகும்.

கேள்வி 12.
a மற்றும் b என்பவை வெவ்வேறு முழுக்கள் எண்கள் எனில், n என்ற மிகை முழு எண்ணிற்கு aⁿ – bⁿ -ன் ஒரு காரணி a – b என நிறுவுக. (குறிப்பு : aⁿ = (a – b + b)ⁿ என எடுத்து விரிவுபடுத்துக.)
தீர்வு:
a = a + b – b = b + (a – b)
∴ aⁿ = [b + (a – b)]ⁿ
ஈருறுப்புத் தேற்றத்தைப் பயன்படுத்தி

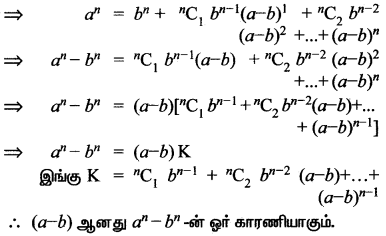
கேள்வி 13.
(a + b)ⁿ-ன் விரிவில், 4 ஆவது மற்றும் 13 ஆவது உறுப்புகளின் கெழுக்கள் சமம் எனில், n-ன் மதிப்பைக் காண்க.)
தீர்வு:
(a + b)ⁿ-ன் பொது உறுப்பு T_{n + 1} = ⁿC_r a^{n – r} b^r …. (1)
4 வது உறுப்பின் கெழுவைக்காண r = 3 என (1) ல் பிரதியிட
∴ T₄ = ⁿC₃ a^{n – 3} b³
வது உறுப்பின் கெழுவைக்காண
r = 12 என (1) ல் பிரதியிட
∴ T₁₃ = ⁿC_r 12^{n – 12} b^12
nC₃ = ⁿC₁₂ எனக் கொடுக்கப்பட்டுள்ளது
⇒ n = 3 + 12 = 15 ⇒ n = 15

கேள்வி 14.
(a + x)ⁿ-ன் விரிவில் தொடர்ச்சியான மூன்று உறுப்புகளின் ஈருறுப்புக் கெழுக்களின் விகிதம் 1:7:42 எனில் n-ன் மதிப்பைக் காண்க.
தீர்வு:
மூன்று அடுத்தடுத்த உறுப்புகள் முறையே
r, (r + 1), (r + 2) என்க


⇒ 6r + 6 = n – r ⇒ n – 7r = 0 ….. (3)
(2) – (3)
(n – 8r + 1) – (n – 7r – 6) = 0
⇒ – r + 7 = 0 ⇒ r = 7
r = 7 என (2) ல் பிரதியிட –
n – 8(7) + 1 = 0
⇒ n – 56 + 1 = 0
⇒ n – 55 = 0 ⇒ n = 55
n = 55 & r = 7

கேள்வி 15.
(1 + x)ⁿ-ன் விரிவில் 5-ஆவது, 6ஆவது மற்றும் 7 ஆவது உறுப்புகளின் கெழுக்கள் ஒரு கூட்டுத் தொடர் எனில், 7-ன் மதிப்புகளைக் காண்க.
தீர்வு:
(1 + x)ⁿ-ன் பொது உறுப்பு
T_{r + 1} = ⁿC_r(1)^{n – r}x^r …… (1)
5 வது, 6வது, 7வது உறுப்பின் கெழுக்களைக் காண r = 4, 5, 6 என (1) ல் பிரதியிட

⇒ 12(n – 4) = 30 + n² – 5n – 4n + 20
⇒ 12n – 48 = 30 + n² – 9n + 20
⇒ n² – 21n + 98 = 0
⇒ n (n – 7) -14 (n – 7) = 0
⇒ (n – 14) (n – 7) = 0
⇒ 14 அல்லது n = 7

கேள்வி 16.
C₀² + C₁² + C₂² + ….. + C_n² = 2n) என நிறுவுக.
தீர்வு: