Samacheer Kalvi 11th Maths Guide Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.2

கேள்வி 1.
தொடர்முறைகளின் n ஆவது உறுப்பு கொடுக்கப் பட்டுள்ளது. அவற்றின் முதல் 6உறுப்புகளைக் காண்க. மேலும், அந்த தொடர் முறைகள், கூட்டுத் தொடர்முறை, பெருக்குத்தொடர்முறை, இசைத்தொடர்முறை, கூட்டு பெருக்குத் தொடர்முறை மற்றும் இவற்றில் எதுவுமில்லை என வகைப்படுத்துக.
(i) \(\frac{1}{2^{n+1}}\)
தீர்வு:

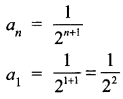
(ii) \(\frac{(n+1)(n+2)}{(n+3)(n+4)}\)
தீர்வு:

இது கூட்டுத் தொடர், பெருக்குத் தொடர் மற்றும் இசைத்தொடர்முறை ஏதுமில்லை.

(iii) \(4\left(\frac{1}{2}\right)^{n}\)
தீர்வு:

(iv) \(\frac{(-1)^{n}}{n}\)
தீர்வு:

(v) \(\frac{2 n+3}{3 n+4}\)
தீர்வு:

(vi) 2018
தீர்வு:
aⁿ = 2018 என்க
முதல் 6 உறுப்புகள் = 2018, 2018, 2018, 2018, 2018, 2018
இங்கு பொது வித்தியாசம், பொது விகிதம் சமமாக உள்ள தால் இது A.P, G.P, AGP ஆகும்.

(vii) \(\frac{3 n-2}{3^{n-1}}\)
தீர்வு:

கேள்வி 2.
1 ஆவது உறுப்பு . ஐக் கொண்ட பின்வரும் தொடர்முறைகளின் முதல் 6 உறுப்புகளைக் காண்க.

தீர்வு:
a₁ = 1 + 1 = 2
a₂ = 2
a₃ = 3 + 1 = 4
a₄ = 4
a₅ = 5 + 1 = 6
a₆ = 6
முதல் 6 உறுப்புகள் 2, 2, 4, 4, 6, 6, …….

(ii)

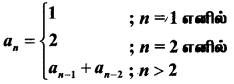
தீர்வு:
a₁ = 1
a₂ = 2
a₃ = 3
a₄ = 2 + 3 = 5
a₅ = 3 + 5 = 8
a₆ = 5 + 8 = 13
∴ முதல் 6 உறுப்புகள் 1, 2, 3, 5, 8, 13,..

(iii)

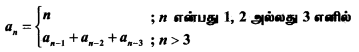
தீர்வு:
a₁ = 1
a₂ = 2
a₃ = 3
a₄ = a₁ + a₂ + a₃ = 3 + 2 + 1 = 6
a₅ = a₂ + a₃ + a₄ = 6 + 3 + 2 = 11
a₆ = a₃ + a₄ + a₅ = 11 + 6 + 3 = 20
முதல் 6 உறுப்புகள் 1, 2, 3, 6, 11, 20, …..

கேள்வி 3.
பின்வரும் தொடர்முறைகளின் 7-ஆவது உறுப்பு காண்க.
(i) 2, 2, 4, 4, 6,6…
தீர்வு:
2, 2,4,4,6,6,….
∴ ஒற்றைப்படை உறுப்புகள் 2, 4, 6,….
இரட்டைப்படை உறுப்புகள் 2,4,6,….

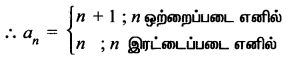
(ii) \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots\)
தீர்வு:
தொகுதியில் உள்ள உறுப்புகளை கவனிக்க.
1, 2, 3, …….
a = 1, d = 2 – 1 = 1 ⇒ a_n = a + (n – 1) d
a_n = 1 + (n + 1)1 = n
பகுதியில் உள்ள உறுப்புகளை கவனிக்க.
= 2, 3, 4, 5, 6, …
இங்கு a = 2, d = 1
∴ a = 2 + (n – 1) = n + 1
கொடுக்கப்பட்ட தொடரின் 7-ம் உறுப்பு
= \(\frac{n}{n+1}\) ∀ n ∈ N

(iii) \(\frac{1}{2}, \frac{3}{4}, \frac{5}{6}, \frac{7}{8}, \frac{9}{10} \ldots\)
தீர்வு:
தொகுதி = 1,3,5,7,9,
a = 1, d = 3 – 1 = 2
∴ a_n = 1 + (n – 1)2 = 2n – 1
பகுதி = 2, 4, 6, 8, 10,…
a = 2, d = 4 – 2 = 2
∴ a_n = 2 + (n – 1)2 = 20
கொடுக்கப்பட்ட தொடரின் 7-ம் உறுப்பு \(\frac{2 n-1}{2 n}\) ∀ n ∈ N

(iv) 6, 10, 4, 12, 2, 14, 0, 16, -2,….
தீர்வு:
6, 10, 4, 12, 2, 14, 0, 16, -2, …..
ஒற்றை உறுப்புகள் = 6, 4, 2, 0, -2, ….
t_n = 6 + (n – 1) (-2) = 6 – 2n + 2
= 8 – 2n
இரட்டை உறுப்புகள் = 10, 12, 14, 16,….
∴ = 10 + (n – 1)2 = 10 + 2n – 2 = 8 + 2n

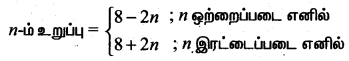
கேள்வி 4.
ஏறு வரிசையில் பெருக்குத்தொடர் முறையில் உள்ள மூன்று உறுப்புகளின் பெருக்கல் 5832. இரண்டாவது எண்ணுடன் ஐெயும் மூன்றாவது எண்ணுடன் 9 ஐயும் கூட்டக் கிடைக்கும் எண்கள் ஒரு கூட்டுத் தொடர்முறையாக இருக்கும் எனில், பெருக்குத் தொடர் முறையின் அந்த மூன்று எண்களைக் காண்க.
தீர்வு:

கேள்வி 5.
\(\frac{3}{1^{2} 2^{2}}, \frac{5}{2^{2} 3^{2}}, \frac{7}{3^{2} 4^{2}}\) —என்ற தொடரின் 7-ஆவது உறுப்பினை இரு உறுப்புகளின் வித்தியாசமாக எழுதுக.
தீர்வு:
தொகுதியில் உள்ள உறுப்புகள் 3, 5, 7 …… AP.
∴ t_n = 3 + (n – 1)2 = 2n + 1 [a = 3, d = 2]
பகுதியில் உள்ள உறுப்புகள் = 1² 2², 2² 3², 3² 4², ……
∴ t_n = [n (n + 1)]²
∴ n-ம் உறுப்பு

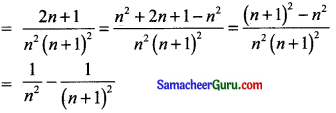
கேள்வி 6.
ஒரு பெருக்குத் தொடர்முறையின் k ஆவது உறுப்பு
t_k எனில், k-ன் எல்லா மிகை முழு எண்ணுக்கும் t_n-k, t_n+k என்பனவும் ஒரு பெருக்குத் தொடர்களே என நிறுவுக.
தீர்வு:
t_k என்பது பெருக்குத் தொடரின் k ஆவது உறுப்பு.

(1) = (2) பொது விகிதம் சமம்
∴ இது ஒரு பெருக்குத் தொடர்.

கேள்வி 7.
a, b, c என்பன ஒரு பெருக்குத் தொடர் முறையாக இருந்து \(a^{\frac{1}{x}}=b^{\frac{1}{y}}=c^{\frac{1}{z}}\) எனவும் இருக்குமானால், x, y, z என்பன ஒரு கூட்டுத் தொடர் முறையாகும் என நிறுவுக.
தீர்வு:
\(a^{\frac{1}{x}}=b^{\frac{1}{y}}=c^{\frac{1}{z}}\) என கொடுக்கப்பட்டுள்ளது.
⇒ a = k^x, b = k^y, c = k^z
a, b, c. ஒரு பெருக்குத் தொடர்
\(\frac{b}{a}=\frac{c}{b}\) ⇒ b² = ac
⇒ (k^y)² = (k^x) (k^z) ⇒ k^2y = k^x+z
⇒ 2y = x + z ⇒ y + y = x + z
⇒ y – x = z – y
x, y, z பொது வித்தியாசம் சமம்.
∴ x, y, z ஒரு கூட்டுத் தொடர் முறை ஆகும்.

கேள்வி 8.
இரு எண்களின் கூட்டுச் சராசரியானது, பெருக்குச் சராசரியைவிட 10 அதிகமாகவும், இசைச் சராசரியை விட 16 அதிகமாகவும் இருக்குமானால் அந்த இரு எண்களைக் காண்க.
தீர்வு:

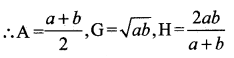
கேள்வி 9.
(q – r)x² + (r – p)x + (p – q) = 0 என்ற சமன்பாட்டின் மூலங்கள் சமமானவை எனில் p, q, r என்பன ஒரு கூட்டுத் தொடர் முறையாக இருக்கும் என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட சமன்பாடு
(q – r) x² + (r – p) x + (p – q) = 0
a = q – r, b = r – p, c = p – q
இருபடிச் சமன்பாட்டின் மூலங்கள் சமம் என்பதால்
b² – 4ac = 0
(r – p)² – 4 (q – r) (p – q) = 0
⇒ r² + p² – 2pr – 4 (pq – pr – q + qr) = 0
⇒ r² + p² – 2pr – 4pq- 4pr – 4q² – 4qr = 0
⇒ r² + p² + 4q² + 2pr – 4pq – 4rq = 0
⇒ (r + p – 2q)² = 0
⇒ r + p – 2q = 0
⇒ 2q = p + r = q – p = r – q
p, q, r-ல் பொது வித்தியாசம் சமம்
∴ p, q, r ஒரு கூட்டுத் தொடர் முறை ஆகும்.

கேள்வி 10.
ஒரு பெருக்குத் தொடரின் p, q மற்றும் 7 ஆவது, உறுப்புகள் முறையே a, b மற்றும் C எனில், (q – r) log a + (r – p) log b + (p – q) log c = 0 என
நிறுவுக.
தீர்வு:
ஒரு G.P-யில்
A முதல் உறுப்பு, R- பொது வித்தியாசம் என்க.
a = P ஆவது உறுப்பு
⇒ a = AR^P-1
⇒ log a = log A + (p – 1) log R …. (1)
b = q ஆவது உறுப்பு ⇒ b = AR^{q – 1}
⇒ log b = log A + (q – 1) log R … (2)
c = r ஆவது உறுப்பு ⇒ c = AR^{r – 1}
⇒ log c = log A + (r – 1) log R … (3)
LHS = (q – r) log a + (r – p) log b + (p – q) log c = (q – r)
[log A + (p – 1) log R] + (r – p)
[log A + (q – 1) log R] + (p – q)
[log A +(r – 1) log R]
= log A