Samacheer Kalvi 11th Maths Guide Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.3 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.3

கேள்வி 1.
ஒரு கூட்டுத் தொடரின் முதல் 10 உறுப்புகளின் ‘கூடுதல் 52 மற்றும் முதல் 15 உறுப்புகளின் கூடுதல் 77 எனில், முதல் 20 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு:
1 உறுப்புகளின் கூடுதல் S_n என்க.
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₀ = 52 கொடுக்கப்பட்டுள்ளது.
⇒ 52 = \(\frac{10}{2}\)[2a + (10 – 1)d]
⇒ 52 = 10a + 45d ……. (1)
S₁₅ = 77 கொடுக்கப்பட்டுள்ளது.
⇒ 77 = \(\frac{15}{2}\)[2a + (15 – 1)d]
⇒ 77 = 15a + 105d …… (2)

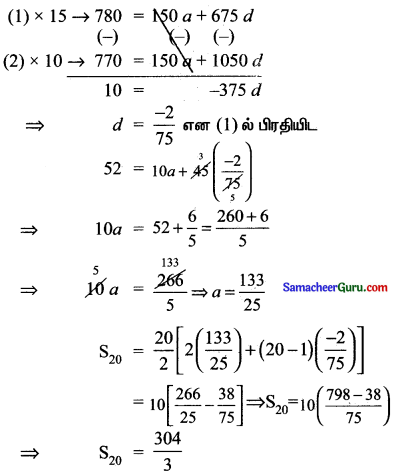
கேள்வி 2.
\(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}\) + …… என்ற தொடரின் முதல் 17 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு:
1 -ம் உறுப்பு T_n என்க.

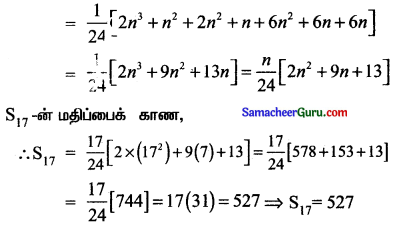
கேள்வி 3.
பின்வரும் தொடர்களின் முதல் 1 உறுப்புகளின் கூடுதல் காண்க.
(i) 8 + 88 + 888 + 8888 …..
(ii) 6 + 66 + 666 + 6666 …..
தீர்வு:
S_n = 8 + 88 + 888 + 8888 + …….
= 8 (1 + 11 + 111 + 1111 + ……)
n உறுப்புகள் கூடுதல் வரை
= \(\frac{8}{9}\)(9 + 99 + 999 + …….)
9 ஆல் பெருக்கி வகுக்க
= \(\frac{8}{9}\) [[10 – 1) + (100 – 1) + (1000 – 1) + …..]
S_n = \(\frac{8}{9}\)[(10¹ + 10² + 10³ + ….. + 10ⁿ)] – (1 + 1 + 1 +…+1, n உறுப்புகள்)]
10¹ + 10² + 10³ + …. + 10ⁿ,
a = 10, r = 10 இது ஒரு G.P.

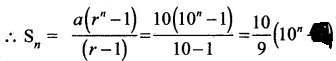
1 + 1 + 1 + ….. n உறுப்புகள் வரை = n
(1) ல் இந்த மதிப்புகளை பிரதியிட

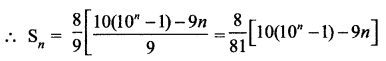
(ii) S = 6 + 66 + 666 + … n உறுப்புகள் வரை
= 6(1 + 11 + 111 +… n உறுப்புகள் வரை )
= \(\frac{6}{9}\) (9 + 99 + 999 + …… n உறுப்புகள் வரை )
(∵ 9 ஆல் பெருக்கி 9 ஆல் வகுக்க)
= \(\frac{6}{9}\)[(10 – 1) + (10² – 1) + (10³ – 1) + ……)
n உறுப்புகள் வரை
= ² (10 + 10² + 10³ + …..) – (1 + 1 + 1 + …..)
n உறுப்புகள் வரை

கேள்வி 4.
1 + (1 + 4) + (1 + 4 + 4²) + (1 + 4 + 4² + 4³) + …..
என்ற தொடரின் முதல் n உறுப்புகளின் கூடுதல் காண்க.
தீர்வு:
7ஆம் உறுப்பு T_n என்க.

கேள்வி 5.
\(\text { 1, } \frac{4}{3}, \frac{7}{9}, \frac{10}{27}, \ldots\) என்ற தொடர் முறையின் nஆவது உறுப்பு மற்றும் முதல் n உறுப்புகளின் கூடுதல் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கூட்டுத் தொடர் தொகுதியில் உள்ள உறுப்புகள் = 1, 4, 7, 10, …
a = 1, d = 3
∴ மவது உறுப்பு = 1 + (n – 1)3 = 3n – 2
பகுதியில் உள்ள உறுப்புகள் = 3, 9, 2, 7
r = \(\frac{1}{3}\)
S_n = \(\frac{a-(a+(n-1) d) r^{n}}{1-r}+d r\left(\frac{1-r^{n-1}}{(1-r)^{2}}\right)\)

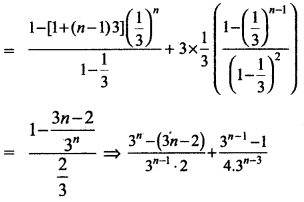
கேள்வி 6.
√3 + √75 + √243 + …. என்ற தொடரின் உறுப்புகளின் கூடுதல் 43573. எனில் 7-ன் மதிப்பு காண்க.
தீர்வு:
√3 + √75 + √243 + ….. கொடுக்கப்பட்ட தொடர்
S_n = 435√31√3 + 5√3 + 9√3 + …….
a = √3, d = 4√3
இது ஒரு A.P ஆகும்.

∴ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ 435√3 = \(\frac{n}{2}\) [2√3 + (n – 1)4√3)
⇒ 435√3 = \(\frac{n}{2}\)√3[2 + (n – 1)4]
⇒ 435 × 2 = n[2+ 4n – 4]
⇒ 435 × 2 = 2 × n[2n – 1]
⇒ 435 = 2n² – n
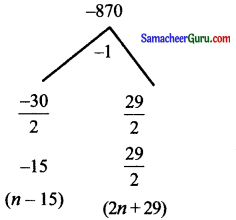
⇒ 2n² – n – 435 = 0
⇒ (2n + 29) (n – 15) = 0
∴ n = –
அல்லது n = 15 (-2) இது பொருந்தாது)
∴ n = 15

கேள்வி 7.
ஒரு கூட்டுத்தொடர் முறையின் (m + n) ஆவது மற்றும் (m – n) ஆவது உறுப்புகளின் கூடுதல் m ஆவது உறுப்பைப் போல் இருமடங்கு என நிறுவுக.
தீர்வு:
T_n = a + (n – 1) d
∴ T_{m + n} = a + (m + n – 1)d
மற்றும் T_{m – n} = a +(m – n – 1)d
LHS T_{m + n} + T_{m – n} = [a + (m + n – 1) d] +
[a+ (m – n – 1) d]
= 2a + (2m – 2) d
= 2 [a + (m – 1) d]
= 2 T_m = RHS

கேள்வி 8.
ஒருவர் ₹3250 என்ற தொகையை முதல் மாதம் ₹20-ம் அடுத்தடுத்த ஒவ்வொரு மாதமும் ₹15 அதிகப்படுத்தியும் செலுத்தி வருகின்றார் எனில், அவர் அந்தத் தொகையை முழுமையாக திருப்பிச் செலுத்த எத்தனை மாதங்கள் ஆகும்?
தீர்வு:
n மாதங்களில் கடன் முழுவதும் தீர்க்கப்படும் எனில் மொத்தத் தொகை ஒரு கூட்டுத்தொடரை அமைக்கும்.
∴ கூட்டுத் தொடரின் கூடுதல் S_n = 3250
⇒ \(\frac{n}{2}\)[2a+(n-1) d] = 3250
⇒ \(\frac{n}{2}\)[40 +(n- 1) 15] = 3250
⇒ n(15n + 25) = 6500
⇒ 15n² + 25n – 6500 = 0
⇒ 3n² + 5n – 1300 = 0
⇒ (3n + 65) (n – 20) = 0
∴ n = \(\frac{-65}{3}\) அல்லது n = 20 = n = 20
∴ மொத்தத் தொகை 20 மாதங்களில் தீர்க்கப்படும்.

கேள்வி 9.
ஒரு பந்தயத்தில் 20 பந்துகள் ஒவ்வொன்றும் 4ம் இடைவெளியில் ஒரே நேர்க்கோட்டில் வைக்கப்படு கின்றன. முதல் பந்திற்கும் தொடக்கப்புள்ளிக்கும் உள்ள இடைவெளி 24ம். ஒரு போட்டியாளர் ஒரு நேரத்தில் ஒரு பந்து வீதம் எல்லா பந்துகளையும் தொடக்கப் புள்ளிக்கு கொண்டு வந்து சேர்க்க எவ்வளவு தூரம் ஓட வேண்டும்.
தீர்வு:
கொடுக்கப்பட்ட தகவலின் படி

முதல் பந்தை எடுக்க பயணித்த தூரம் = 24 + 24 = 48மீ
இரண்டாவது பந்தை எடுக்க பயணித்த துாரம் = 2
2(24 + 4) = 56மீ
மூன்றாவது பந்தை எடுக்க பயணித்த தூரம்
= 2 (24 + 4 + 4) = 64மீ
48, 56, 64, ….. 20
a = 48, d = 56 – 48 = 8 மற்றும் n = 20
எல்லாப் பந்துகளையும் தொடக்கப்புள்ளிக்கு கொண்டு வந்து சேர்க்க போட்டியாளர் ஓடவேண்டிய தூரம் = 20 உறுப்புகளின் கூடுதல்
S_n = \(\frac{n}{2}\)[2a + (n – 1)d] |
∴ S_n = \(\frac{20}{2}\) [2 (48) + 19 (8)]
= 10 [96 + 152] ⇒ S₂₀ = 2480மீ.

கேள்வி 10.
நுண்ணுயிர் வளர்ச்சியில் ஒவ்வொரு மணி நேரத்திற்கும் நுண்ணுயிரிகளின் எண்ணிக்கையானது அதன் முந்தைய மணி நேரத்தில் உள்ளது போல் இரு மடங்காகிறது. ஆரம்பத்தில் 30 நுண்ணுயிர்கள் இருக்குமானால் 2ஆவது 4ஆவது மற்றும் n ஆவது மணிநேர முடிவில் எத்தனை நுண்ணுயிர்கள் இருக்கும்.
தீர்வு:
வெவ்வேறு நேரத்தில் நுண்ணுயிரிகளின் எண்ணிக்கை ஒரு G.P.
a = 30 r = 2
2 ஆவது மணிநேரத்தில் நுண்ணுயிரிகளின் எண்ணிக்கை
t₃ = a. r² = 30 × 2² = 30 × 4 = 120
4 ஆவது மணி நேரத்தில் நுண்ணுயிரிகளின் எண்ணிக்கை
t₃ = a. r⁴ = 30 × 2⁴ = 30 × 16 = 480
n-ஆவது மணி முடிவில் நுண்ணுயிரிகளின் எண்ணிக்கை
t_{n + 1} = a. rⁿ = 30 (2ⁿ)

கேள்வி 11.
ஒரு வங்கியில் செலுத்தப்பட்ட₹ 500 ஆனது, 10% தொடர் வட்டி வீதத்தில், 10 ஆண்டுகளில் எவ்வளவாக மாறும்.
தீர்வு:
P = 1500, R – வட்டி வீதம் = 10%
ஓராண்டு முடிவில் தொகை = \(\left(P+\frac{P R}{100}\right)=P\left(1+\frac{R}{100}\right)\)
இரண்டாம் ஆண்டு முடிவில்

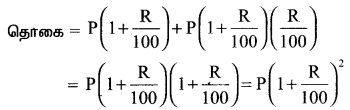
முதல் உறுப்பு மற்றும் பெருக்கு விகிதம் ஒரு G.P.-யை அமைக்கிறது. 10-ஆவது ஆண்டு முடிவில் G.P. யின் தொகை = 11^th உறுப்பு

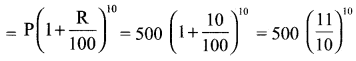
10-ம் ஆண்டு முடிவில் தொகை = 500 (1.1)¹⁰ = 1296.87

கேள்வி 12.
ஒரு நகரத்தில், வைரஸ் நோயினால் ஏற்பட்ட சுகாதார கேட்டினால் மக்களின் இயல்பு வாழ்க்கை பாதிக்கப்பட்டிருந்தது. ஒவ்வொரு நாளும் அந்த நோய் தாக்கும் வைரஸ் கிருமிகள் ஒரு பெருக்குத் தொடர் முறையில் பரவி வருகிறது. இந்த தொற்று கிருமிகள் ஒவ்வொரு நாளும் அதன் முந்தைய நாளைப் போல் இருமடங்காக பெருகுகிறது. முதல் நாளில் அதன் எண்ணிக்கை 5 எனில், அந்த கிருமிகளின் எண்ணிக்கை எந்த நாளில் 1,50,000-க்கு அதிகமாக இருக்கும் எனக் காண்க.
தீர்வு:
a = 5 எனக் கொடுக்கப்பட்டுள்ளது.
தொற்று கிருமிகள் ஒவ்வொரு நாளும் முதல் நாளைப்போல் 2 மடங்கு பெருகுவதால் அது ஒரு G.Pயை அமைக்கிறது. 5, 10, 20, 40, …, 150000

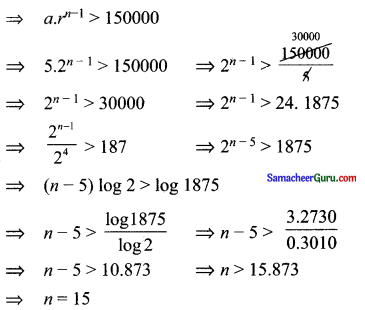
∴ 15-ம் நாள் தொற்றுநோய் கிருமிகள் 1,50;000 க்கு அதிகமாக இருக்கும்.