Samacheer Kalvi 11th Maths Guide Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.4 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 5 சஈருறுப்புத் தேற்றம், தொடர்முறைகள் மற்றும் தொடர்கள் Ex 5.4

கேள்வி 1.
பின்வருவனவற்றை -ன் ஏறுவரிசை அடுக்குகளாக விரிவாக்கம் செய்க. அந்த விரிவு ஏற்புடையதாக இருப்பதற்கான x-ன் நிபந்தனையைக் காண்க.
(i) \(\frac{1}{(5+x)}\)
தீர்வு:

இந்த விரிவு ஏற்புடையதாக இருக்க வேண்டுமெனில்
\(\left|\frac{x}{5}\right|\) < 1 ⇒ |x| < 5 ஆக இருக்க வேண்டும்.

(ii) \(\frac{2}{(3+4 x)^{2}}\)
தீர்வு:

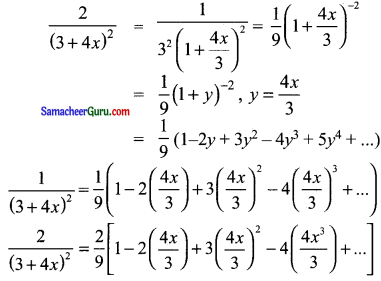
விரிவு ஏற்புடையதாக இருக்க |y | < 1ஆக இருக்க வேண்டும்.
y = \(\frac{4 x}{3}\)
∴ விரிவு ஏற்புடையதாக இருக்க வேண்டுமெனில் \(\left|\frac{4x}{3}\right|\) < 1 ⇒ |x| < \(\frac{3}{4}\) ஆக இருக்க வேண்டும்.

(iii) \(\left(5+x^{2}\right)^{\frac{2}{3}}\)
தீர்வு:

இந்த விரிவு ஏற்புடையதாக இருக்க வேண்டுமெனில் \(\left|\frac{x^{2}}{5}\right|\) < 1 ⇒ x² < 5 இருக்க வேண்டும்.

(iv) \((x+2)^{\frac{-2}{3}}\)
தீர்வு:

கேள்வி 2.
\(\sqrt[3]{1001}\) -ன் மதிப்பைத் தோராயமாக காண்க. (இரு தசமத்திருத்தமாக).
தீர்வு:

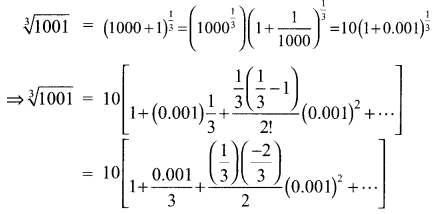
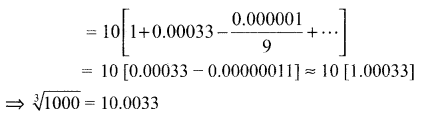
கேள்வி 3.
x ஒரு தேவையான அளவிலான பெரிய எண் எனில், IR +6-3+3 – ன் மதிப்பைத் தோராயமாக என நிறுவுக.
தீர்வு:

கேள்வி 4.
மிகச் சிறியது எனில், \(\sqrt{\frac{1-x}{1+x}}\) என்பது தோராயமாக 1 – x + \(\frac{x^{2}}{2}\) என நிறுவுக.
தீர்வு:

கேள்வி 5.
பின்வரும் அடுக்குக்குறித் தொடரில் முதல் 6. உறுப்புகளைக் காண்க.
(i) e^5x
தீர்வு:

(ii) e^-2x
தீர்வு:

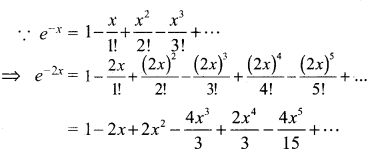
(iii) \(e^{\frac{1}{2} x}\)
தீர்வு:

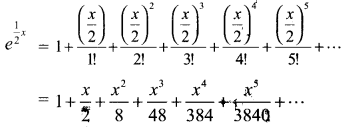
கேள்வி 6.
பின்வரும் மடக்கைத் தொடர்களின் முதல் 4 உறுப்புகளைக் காண்க.
(i) log (1 + 4x)
(ii) log (1 – 2x)
(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)
(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)
இந்த விரிவுகள் ஒவ்வொன்றும் எந்த இடைவெளியில் ஏற்புடையது எனவும் காண்க.
தீர்வு:
(i)

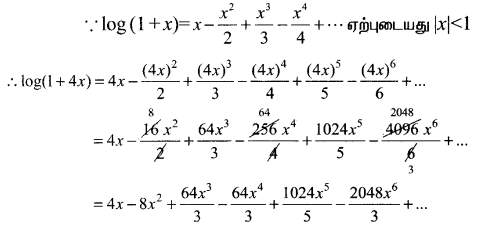
இந்த தொடர் |4x| < 1 ⇒ |x| < \(\frac{1}{4}\) ஆக இருக்கும் போது ஏற்புடையதாக இருக்கும்.
∴ தேவையான இடைவெளி – \(\frac{1}{4}\) < x < \(\frac{1}{4}\)

(ii)


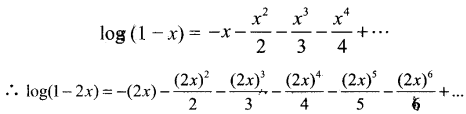
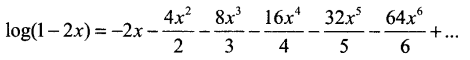
தொடர் |2x| < 1 ⇒ |x| < \(\frac{1}{2}\) ஆக இருக்கும் போது ஏற்புடையதாக இருக்கும்.
∴ ஏற்புடையதான இடைவெளி –\(\frac{1}{2}\) < x < \(\frac{1}{2}\)

(iii)

இந்த தொடர் |3x|< 1 ⇒ |x| < \(\frac{1}{3}\) ஆக இருக்கும் போது
∴ ஏற்புடைய இடைவெளி –\(\frac{1}{3}\) < x < \(\frac{1}{3}\)

(iv)

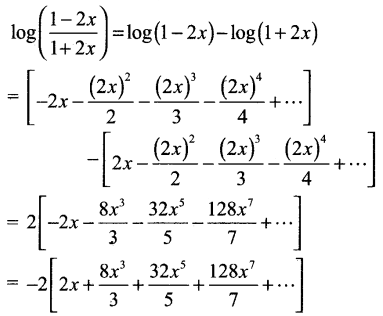
தொடர் ஏற்புடையதாக இருக்க |2x| < 1 ⇒ |x| < \(\frac{1}{2}\) இருக்க வேண்டும்
∴ ஏற்புடையதாக இருக்கும் இடைவெளி –\(\frac{1}{2}\) < x < \(\frac{1}{2}\)

கேள்வி 7.
y = \(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4}+\ldots\) எனில்,
x = \(y-\frac{y^{2}}{2 !}+\frac{y^{3}}{3 !}-\frac{y^{4}}{4 !}+\ldots\) என நிறுவுகள்
தீர்வு:
y = \(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\frac{x^{4}}{4}+\ldots\) என கொடுக்கப்பட்டுள்ளது.
இருபுறமும் (-1) ஆல் பெருக்க

கேள்வி 8.
p மற்றும் ஏ ஐ ஒப்பிடும் போது, p – q சிறியது எனில், \(\sqrt[n]{\underline{p}} \simeq \frac{(n+1) p+(n-1) q}{(n-1) p+(n+1) q}\) என நிறுவுக. இதன் மூலம் \(\sqrt[8]{\frac{15}{16}}\) -ன் மதிப்பினைக் காண்க.
தீர்வு:
p = q + h என்க.
h மிகச் சிறிய மதிப்புடையதால் h², h³ நீக்கப்படலாம்.

கேள்வி 9.
\(\frac{3-4 x+x^{2}}{e^{2 x}}\)-ன் விரிவில் x^4</-ன் கெழுவைக் காண்க.
தீர்வு:

கேள்வி 10.
மதிப்புக் காண்க.

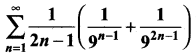
தீர்வு: