Samacheer Kalvi 11th Maths Guide Chapter 6 இருபரிமாண பகுமுறை வடிவியல் Ex 6.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 இருபரிமாண பகுமுறை வடிவியல் Ex 6.2 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 6 இருபரிமாண பகுமுறை வடிவியல் Ex 6.2

கேள்வி 1.
கீழ்க்காணும் விவரங்களுக்கு , (1, 1) என்ற புள்ளி வழியே செல்லக்கூடிய நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.
(i) y-ன் வெட்டுத்துண்டு (4)
(ii) சாய்வு 3
(iii) (-2, 3) என்ற புள்ளி
(iv) ஆதிப்புள்ளியிலிருந்துகோட்டிற்கு வரையப்படும் செங்குத்து கோடு X-அச்சுடன் ஏற்படுத்தும்
கோணம் 60°
தீர்வு:
y வெட்டுத்துண்டு (4)
(i) y வெட்டுத்துண்டும் ஒரு புள்ளியும் கொடுக்கப் பட்டால் கோட்டின் சமன்பாடு y = mx + c
ஒரு புள்ளி (1, 1), y வெட்டுத்துண்டு (-4) அதாவது (0, -4)
∴ சாய்வு = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-4-1}{0-1}=\frac{-5}{-1}=5\)
∴ தேவையான சமன்பாடு y = 5x – 4
(m = 5, c = -4)

(ii) சாய்வு 3
ஒரு புள்ளியும் சாய்வும் கொடுக்கப்பட்டால் சமன்பாடு
y – y₁ = m (x – x₁)
∴ m = 3, (x₁, y₁) = (1, 1)
⇒ சமன்பாடு y – 1 = 3 (x – 1)
y – 1 = 3x – 3
3x – y – 2 = 0

(iii) புள்ளி (-2, 3) வழியாகவும் (1, 1) வழியாகவும் செல்லும் கோட்டின் சமன்பாடு இரு புள்ளிகள் கொடுக்கப்பட்டால் கோட்டின் சமன்பாடு

⇒ -3y + 3 = 2x – 2
⇒ 2x + 3y = 3 + 2
⇒ 2x + 3y = 5

(iv) ஆதிப்புள்ளியிலிருந்து ஒரு புள்ளி P(1, 1)
α = 60° கொடுக்கப்பட்டுள்ளது
செங்குத்துத்தூரம் = OP

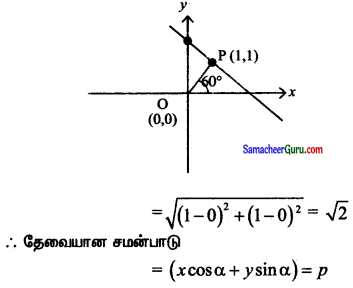
கேள்வி 2.
ஆய அச்சுகளுக்கு இடையே ஒரு கோட்டுத் துண்டின் மையப்புள்ளி P(r, c) எனில் அந்த நேர்க்கோட்டின் \(\frac{x}{r}+\frac{y}{c}\) = 2 எனக் காட்டுக.
தீர்வு:
A, B என்பன இருபள்ளிகள் அவற்றின் அச்சுத் தொலைவுகள்
A(x, 0), B(0, y) எனகொடுக்கப்பட்டுள்ளது.

கேள்வி 3.
(1, 5) என்ற புள்ளி வழியாகவும், ஆய அச்சுகளை 3:10 என்ற விகிதத்தில் பிரிக்கக்கூடிய கோட்டின் சமன்பாட்டைக் காண்க.
தீர்வு:
தேவையான கோட்டின் சமன்பாடு \(\frac{x}{a}+\frac{y}{b}\) = 1 இது
x அச்சை A என்ற புள்ளியிலும் y அச்சை B-யிலும் சந்திக்கிறது.
P(1,5) என்ற புள்ளி AB ஐ 3:10 என்ற விகிதத்தில் பிரிக்கிறது எனில் P-ன் அச்சுத் தொலைவு

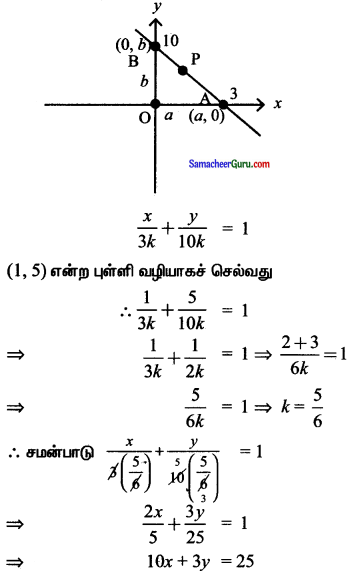
கேள்வி 4.
ஆதியிலிருந்து கோட்டிற்கு இடையே உள்ள செங்குத்து தொலைவு ஆகும். மற்றும் ம் என்பன ஆய அச்சுகளின் வெட்டுத்துண்டின் நீளங்கள் எனில், \(\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\) என நிறுவுக.
தீர்வு:
\(\frac{x}{a}+\frac{y}{b}\) = 1 ⇒ \(\frac{x}{a}+\frac{y}{b}\)– 1 = 0 என்பது வெட்டுத்துண்டு
a b வடிவ சமன்பாடு.
P ஆனது ஆதிப்புள்ளி O(0, 0) விலிருந்து சமன்பாடு (1) ற்கு வரையப்படும் குத்துக்கோடு ஆகும்.

கேள்வி 5.
நீரின் இயல்பான கொதிநிலை 100°C அல்லது 212°F மற்றும் அதன் உறைநிலை 0 C அல்லது 32°F ஆகும்.
(i) வெப்பநிலை C-க்கும் F-க்கும் இடையே உள்ள நேரிய தொடர்பின் சமன்பாட்டைக் காண்க. மேலும்,
(ii) வெப்பநிலை 98.6° F எனில் C-இன் மதிப்பு என்ன ?
(ii) வெப்பநிலை 38 C எனில் F-இன் மதிப்பு என்ன?
தீர்வு:
(i) வெப்பநிலை C-க்கும் F-க்கும் இடையே உள்ள நேரிய தொடர்பின் சமன்பாடு

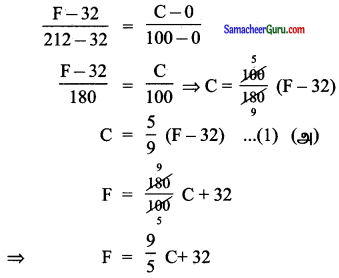
(∴ C செல்சியஸ் வெப்பநிலையையும், F பாரன்ஹீட் வெப்பநிலையையும் குறிக்கிறது.)

(ii) F = 98.6° எனில் C = ?
C-ன் மதிப்பை காண (1) பிரதியிட
⇒ c = \(\frac{5}{9}\)(98 – 6 – 32)
= \(\frac{5}{9}\)(66.6) = \(\frac{333}{9}\) = 37°

(iii) C = 38° எனில் F = ?
F-ன் மதிப்பை காண (1)-ல் பிரதியிட
⇒ 38 = \(\frac{5}{9}\)(F – 32)
⇒ \(\frac{38 \times 9}{5}\) = F – 32 ⇒ \(\frac{342}{5}\) + 32 =F
⇒ F = 68.4 + 32
⇒ F = 100.4° C

கேள்வி 6.
ஒரு பொருளை P என்ற இடத்திலிருந்து ஒரு இலக்கைத் தாக்கச் சீரான வேகத்தில் ஏவப்படுகிறது. அது இலக்கைத தாக்குவதற்கு 15 வினாடிக்கு முன் 1400 மீட்டர் தூரத்திலும் மற்றும் 18ஆவது வினாடியில் 800 மீட்டர் தூரத்திலும் இருக்கிறது எனில்,
(i) இலக்கிற்கும் அந்த இடத்திற்கும் இடைப்பட்ட, தொலைவு என்ன?
(ii) 15ஆவது வினாடியில் எவ்வளவு தொலைவு கடந்திருக்கும்?
(iii) இலக்கைத் தாக்க எடுத்துக் கொள்ளும் நேரம் எவ்வளவு?
தீர்வு:
(i)

d என்பது இலக்கிற்கும் இடத்திற்கும் இடைப்பட்ட தொலைவு என்க.

⇒ 6(d – 1400) = 5 (d – 800)
⇒ 6d – 8400 = 5d – 4000
d = 1400 மீ

(ii) 15 வது வினாடியில் கடந்த தொலைவு:

இருபுள்ளி வடிவம் சூத்திரத்தைப் பயன்படுத்தி

(iii) இலக்கை தாக்க எடுத்துக் கொள்ளும் நேரம்
T₁(15 ஆவது வினாடி) D₁(1400 மீ)
T₂(18 ஆவது வினாடி) D₂(800 மீ)
இரு புள்ளி வடிவம் பயன்படுத்தி

D = 0 என (1)-ல் பிரதியிட.
T = \(\frac{1400-0}{200}\) + 15 = 7 + 15 = 22 வினாடிகள்

கேள்வி 7.
ஒரு நகரத்தில் மக்கள் தொகை 2005 மற்றும் 2010 ஆம் ஆண்டுகளில் முறையே 1,35,000 மற்றும் 1,45,000 எனில், 2015ஆம் ஆண்டு மக்கள் தொகையை தோராயமாகக் காண்க. (மக்கள் தொகையின் வளர்ச்சி ஒரு மாறிலி).
தீர்வு:
x என்பது வருடங்களின் எண்ணிக்கையையும், y என்பது மக்கள் தொகையையும் குறிக்கிறது எனக் கொள்வோம்.
x₁(2005) y₁(1,35,000)
x₂ (2010) y₂(1,45,000)
இரு புள்ளி வடிவம், x.yற்கு இடைப்பட்ட தொடர்பு

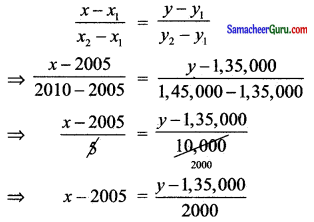
2000 (x – 2005) = y – 1,35,000
∴ y = 2000 (x – 2005) + 1,35,000 …. (1)
2015-ம் ஆண்டு மக்கள் தொகையைக் காண்க.
x = 2015 (1) பிரதியிட
y = 2000 (2015 – 2005) + 1,35,000
= 2000(10) + 1,35,000
= 20000 + 1,35,000
= 1,55,000
2015-ம் ஆண்டு மக்கள் தொகை = 1,55,000

கேள்வி 8.
ஒரு நேர்க்கோட்டிற்கு ஆதியிலிருந்து வரையப்படும் செங்குத்துக் கோட்டின் நீளம் 12 அலகுகள், அச்செங்குத்துக்கோடு – அச்சுடன் ஏற்படுத்தும் கோணம் 30° எனில், அந்த நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்டது α = 30,. P = 12
நேர்கோட்டின் சமன்பாடு = x cos α + y sin α = p

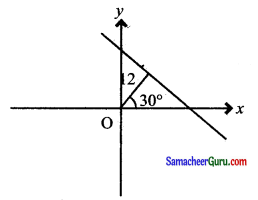
⇒ x cos 30° + y sin 30° = 12
⇒ \(x\left(\frac{\sqrt{3}}{2}\right)+y\left(\frac{1}{2}\right)\) = 12 ⇒ \(\frac{\sqrt{3} x+y}{2}\) = 12
⇒ √3x + y = 24

கேள்வி 9.
(8, 3) என்ற புள்ளி வழியே செல்லக்கூடியதும் ஆய அச்சுகளின் வெட்டுத் துண்டுகளின் கூடுதல் 1 எனில், நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.
தீர்வு:
வெட்டுத்துண்டு வடிவம் \(\frac{x}{a}+\frac{y}{b}\) = 1 ….(1)
கொடுக்கப்பட்டது a + b = 1 ⇒ b = 1 – a
⇒ \(\frac{x}{a}+\frac{y}{1-a}\) = 1
(8, 3) இக்கோட்டின் மீது அமைவதால் நமக்குக் கிடைப்பது.

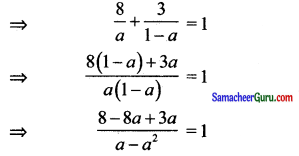
⇒ 8 – 8a + 3a = a – a²
⇒ 8 – 8a + 3a – a + a² = c
a² – 6a + 8 = 0
⇒ (a – 4) (a – 2) = 0 ⇒ a = 4 (அ) 2
a = 4 எனில் b = 1 – 4 = -3
a = 2 எனில் b = 1 – 2 = -1
a = 4, b = -3 எனில் நேர்க்கோட்டின் சமன்பாடு
\(\frac{x}{4}+\frac{y}{-3}=1\) = 1
⇒ -3x + 4y = -12 ((1)ன் மூலம்)
⇒ -3x – 4y = 12
a = 2, b = -1 எனில் \(\frac{x}{2}+\frac{y}{-1}\) = 1
⇒ -x + 2y = -2 ⇒ x – 2y = 2

கேள்வி 10.
(1, 3), (2, 1) மற்றும் \(\left(\frac{1}{2}, 4\right)\) ஆகிய புள்ளிகள் ஒரு கோடமை புள்ளிகள் என,
(i) சாய்வு முறையில்
(ii) நேர்க்கோட்டு முறை மற்றும்
(iii) வேறு ஏதேனும் முறையில் காண்பி.
தீர்வு:
(i) சாய்வு முறை
A(1, 3), 5(2, 1), C\(\left(\frac{1}{2}, 4\right)\) கொடுக்கப்பட்ட புள்ளிகள்
AB -ண் சாய்வு = \(\frac{1-3}{2-1}=\frac{-2}{1}\) (∵ m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\))

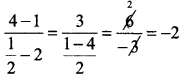
∴ AB-ன் சாய்வு = BC-ன் சாய்வு
∴ AB || BC, B-ன் பொதுப்புள்ளி
∴ A,B,C ஒரே கோட்டில் அமையும்.

(ii) நேர்கோட்டு முறை மற்றும்
AB-ன் சமன்பாடு

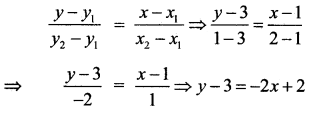
= 2x + y – 5 = 2x + y – 5 = 0
C\(\left(\frac{1}{2}, 4\right)\) ஐ பிரதியிட
2\(\left(\frac{1}{2}\right)\) + 4 – 5 = 1 + 4 – 5 = 0
∴ A, B, C என்பன ஒரே கோட்டில் அமைவன என நிரூபிக்கப்பட்டது.

(iii) வேறு ஏதேனும் முறை

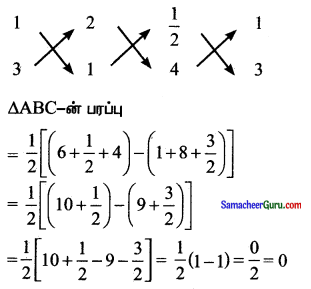
∴ ∆ABC-யின் பரப்பு = 0,
∴ A, B, C ஒரே கோட்டில் அமையும் புள்ளிகள் ஆகும்.

கேள்வி 11.
A (1, 2) என்ற புள்ளி வழியாகவும் \(\frac{5}{12}\) சாய்வைக் கொண்ட நேர்க்கோட்டின் மீது, A என்ற புள்ளியிலிருந்து 13 அலகுகள் தூரத்தில் நேர்க்கோட்டின் மேலுள்ள புள்ளிகளைக் காண்க.
தீர்வு:
நேர்க்கோட்டின் சமன்பாடு y – y₁ = m(x – x₁)
A(1, 2), m = \(\frac{5}{12}\) நேர்க்கோட்டின் சமன்பாடு y – 2 = \(\frac{5}{12}\) (x – 1)
⇒ 12y – 24 = 5x – 5
⇒ 5x – 12y + 24 – 5 = 0
⇒ 5x – 12y + 19 = 0
x = 13 அலகுகள் எனில்
5(13) – 12y + 19 = 0
65 – 12y + 19 = 0
-12y = -65 – 19)
12y = 84
y = 7
∴ (13, 7) தேவையான புள்ளியாகும்.

கேள்வி 12.
150 மீட்டர் நீளமுள்ள தொடர் வண்டி வினாடிக்கு 12.5 மீ நிலையான திசைவேகத்தில் செல்கிறது.
(i) தொடர் வண்டி இயக்கத்தின் சமன்பாடு என்ன?
(ii) ஒரு கம்பத்தைக் கடந்து செல்ல எடுத்துக் கொள்ளும் நேரம் என்ன?
(iii) 850 மீட்டர் நீளம் கொண்ட பாலத்தைக் கடந்து செல்ல எடுத்துக் கொள்ளும் நேரம் என்ன?
தீர்வு:
(i) தொடர்வண்டி இயக்கத்தின் சமன்பாடு X அச்சை நேரத்தை (விநாடிகளில்)யும், y அச்சை தொலைவை (மீட்டரிலும்) குறிப்பதாகக் கொள்வோம்,
தொடர்வண்டி ஆதிப்புள்ளி என்க.
தொடர்வண்டியின் நீளம் =150 மீ. இது ஒரு குறை மதிப்பு
சாய்வு = 12.5 மீ / வினாடி
வண்டியின் நிலையின் திசைவேகம் = 12.5 மீ/ வினாடி
சாய்வும் y வெட்டுத்துண்டும் கொடுக்கப் பட்டுள்ளதால் சமன்பாடு ⇒ y = mx – c
∴ தொடர்வண்டியின் இயக்கச் சமன்பாடு
⇒ y = 12.5x – 150 ….(1)

(ii) ஒரு கம்பத்தைக் கடத்து செல்ல எடுத்துக் ! கொள்ளும் y = 0 நேரம்
⇒ ∴ 12.5x = 150
⇒ x = \(\frac{150}{12 \cdot 5}\) = 12 = 12 வினாடிகள்

(iii) 850 மீ. நீளமுள்ள பாலத்தைக் கடக்க எடுத்துக் கொள்ளும் நேரம்
850 = 12.5x – 150
⇒ 850 + 150 = 12.5x
⇒ x = \(\frac{1000}{12 \cdot 5}\)
⇒ x = 80 வினாடிகள்

கேள்வி 13.
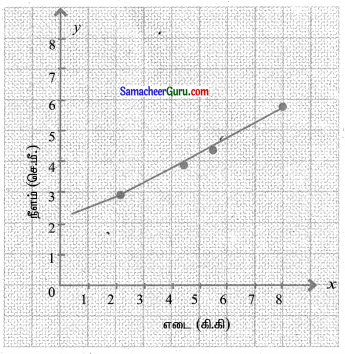
ஒரு அறிவியல் சோதனைக்காக, ஒரு சுருள் வளை கம்பி, (spring) ஒரு கொக்கியில் கட்டித் தொங்கவிடப்பட்டுள்ளது. சுருள் வளை கம்பியின் ! வெவ்வேறு எடைகள் இணைக்க சுருள் வளை கம்பியின் நீளம் அட்டவணையில் உள்ளவாறு நீளுகிறது எனில்,

(i) விளைவுகளை காட்டும் வரைபடம் வரைக.
(ii) சுருள் வளை கம்பியின் நீளம் மற்றும் எடைக்கு உள்ள தொடர்புடைய சமன்பாட்டைக் காண்க.
(iii) சுருள் வளை கம்பியின் உண்மையான நீளத்தைக் காண்க.
(iv) சுருள் வளை கம்பி 9 செ.மீ. நீளம் அடைய வேண்டும் எனில் எவ்வளவு எடை இணைக்க வேண்டும்?
(v) 6 கி.கி. எடையை இணைக்க சுருள்வளைக் கம்பியின் நீளம் என்ன?
தீர்வு:
(i) விளைவுகளை காட்டும் வரைபடம்

(ii) சுருள் வளை கம்பியின் நீளம் மற்றும் எடைக்கு உள்ள தொடர்புடைய சமன்பாடு.

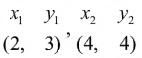
இருபுள்ளிகள் கொடுக்கப்பட்டால் சமன்பாடு

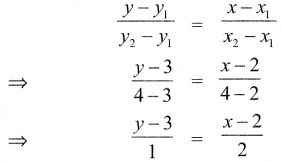
⇒ 2y – 6 = x – 2
⇒ x – 2y + 4 = 0 ….. (1)

(iii) சுருள் வளைக் கம்பியின் உண்மையான நீளம்
x = 0 என்க
⇒ 0 – 2y + 4 = 0
⇒ -2y = -4
⇒ y = 2 செ.மீ.

(iv) சுருள் வளை கம்பி 9 செ.மீ. நீளம் அடைய வேண்டும் எனில் எவ்வளவு எடை இணைக்க வேண்டும்?
y = 9 என (x -2y + 4 = 0)-ல் பிரதியிட
x – 2(9) + 4 = 0
x = 18– 4 = 14 கி.கி.
சுருள் வளை கம்பி 9 செ.மீ. நீளம் அடைய வேண்டும் எனில் 14 கி.கி. எடையை இணைக்க வேண்டும்.

(v) 6 கி.கி. எடையை இணைக்க சுருள்வளைக் கம்பியின் நீளம் என்ன?
x = 6
என (x – 2y + 4 = 0)-ல் பிரதியிட
⇒ 6 – 2y + 4 = 0
-2y = – 10
y = 5 செ.மீ.
6 கி.கி. எடையை இணைக்க சுருள் வளைக் கம்பியின் நீளம் = 5 செ.மீ.

கேள்வி 14.
ஒரு குடும்பம் 14.2 கிகி எடை கொண்ட சமையல் எரிவாயுவினை (LPG) (உருளையின் எடையுடன் 29.5 கிகி) சீரான முறையில் பயன்படுத்தும்போது 24-வது நாளில் சமையல் எரிவாயுத் தீர்ந்து விடுகிறது. உடனடியாக புதிய எரிவாயு உருளை இணைக்கப்படுகிறது.
(i) உருளையிலுள்ள சமையல் எரிவாயுவின் அளவிற்கும் மற்றும் பயன்படுத்தப்பட்ட நாட்களுக்கும் உள்ள தொடர்புடைய சமன்பாட்டைக் காண்க.
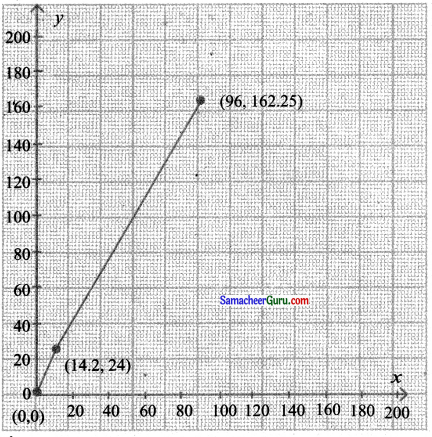
(ii) சமையல் எரிவாயுவினை முதல் 96 நாட்கள் பயன்படுத்துவதற்கான வரைபடம் வரைக.
தீர்வு:
x ஐ சமையல் வாயுவின் எடை எனவும் y ஐ நாட்களின் எண்ணிக்கை எனவும் கொள்க.

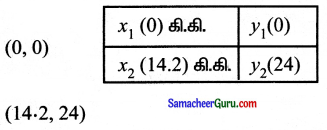
(i) இரு புள்ளி வடிவம் சூத்திரத்தைப் பயன்படுத்தி, சமையல் எரிவாயுவின் அளவிற்கும் பயன்படுத்தப்பட்ட நாட்களுக்கும் உள்ள தொடர்புடைய சமன்பாட்டை அடையலாம்.

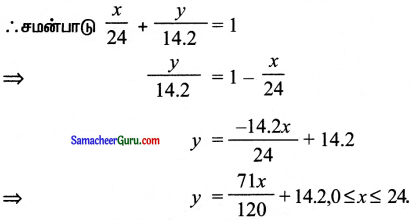
(ii) முதல் 96 நாட்களுக்கான வரைபடம்

x = f(x) என்பது காலத்தைப் பொறுத்தது 24 f(x) = f(x + 24)

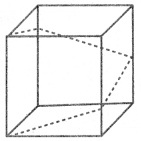
கேள்வி 15.
800 × 800 × 720 அலகுகள் பரிமாணம் கொண்ட கனசெவ்வக வடிவம் கொண்ட ஒரு பேரங்காடியில், படத்தில் கண்டவாறு புள்ளியிட்ட பாதையில் நகரும் படிக்கட்டு (escalator) அமைக்க உத்தேசிக்கப்பட்டுள்ளது எனில்,
(i) நகரும் படிக்கட்டின் மொத்த மீச்சிறு நீளத்தினைக் காண்க.
(ii) எந்தெந்த உயரத்தில் நகரும் படிக்கட்டானது திரும்புகின்றது எனக் காண்க.
(iii) நகரும் படிக்கட்டுகள் திரும்பும் இடங்களில் அதன் சாய்வுகளைக் காண்க.

தீர்வு:
(i) நகரும் படிக்கட்டின் மொத்த மீச்சிறு நீளம் பேரங்காடியின் வடிவம் ஒரு கனச் செவ்வகம். கனச் செவ்வகத்தை பிரித்தால் அதன் தளமானது கீழ்கண்டவாறு அமையும்.

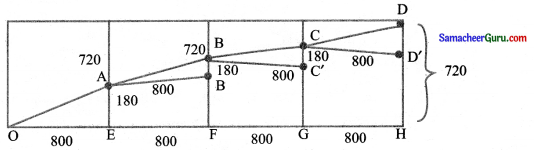
நகரும் படிக்கட்டின் பாதையானது OA விலிருந்து AB, AB யிலிருந்து BC க்கு, BC யிலிருந்து CD க்கும் செல்கிறது எனில் ∆OAE-யில் OA² = AE² + OE²
⇒ OA² = [\(\frac{1}{4}\)(720)]² + OE²
OA² = 180² + 800²
= (20 × 9)² + (20 × 40)²
= 20² (9² + 40²)
= 20²(1681) = 20² (41²)
⇒ OA = 20 × 41 = 820
∴ நகரும் படிக்கட்டின் மொத்த நீளம்
= OA + AB + BC + CD
= 4 × OA = 4 × 820
மீச்சிறு நீளம் = 3280 அலகுகள்

(ii) எந்தெந்த உயரத்தில் நகரும் படிக்கட்டானது திரும்புகின்றது.
நகரும் படிக்கட்டு திரும்புகின்ற உயரம்
AE = \(\frac{1}{4}\)(720) = 180 அலகுகள்
BE = \(\frac{1}{2}\)(720) = 180 அலகுகள்
GE = \(\frac{3}{4}\)(720) = 180 அலகுகள்

(iii) நகரும் படிக்கட்டுகள் திரும்பும் இடங்களில் அதன் சாய்வுகள்.
∠AOE = θ என்க.
∆OAE-ல்

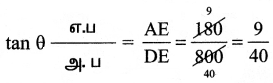
A என்ற புள்ளியின் சாய்வு =\(\frac{9}{40}\)
∆OAE = ∆ABB’ = ∆BCC’ = ∆CDD’
∴ BC என்ற புள்ளிகளில் சாய்வு \(\frac{9}{40}\)