Samacheer Kalvi 11th Maths Guide Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.1 Textbook Questions and Answers, Notes.

TN Board 11th Maths Solutions Chapter 7 கணங்கள், தொடர்புகள் மற்றும் சார்புகள் Ex 7.1

Question 1.

(i) a_ij = \(\frac{(i-2 j)^{2}}{2}\) m = 2, n = 3
(ii) a_ij = \(\frac{|3 i-4 j|}{4}\), m = 3, n = 4 என இருக்குமாறு: உறுப்புகளைக் கொண்ட m x n வரிசை உடைய A = [a_ij] அணிகளை உருவாக்குக.
தீர்வு:
(i) a_ij = \(\frac{(i-2 j)^{2}}{2}\) m = 2, n = 3
A = \(\left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right)\)

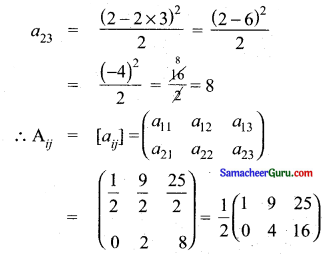
(ii) a_ij = \(\frac{|3 i-4 j|}{4}\), m = 3, n = 4
A = \(\left(\begin{array}{llll}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & b_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34}
\end{array}\right)\)

Question 2.
\(\left[\begin{array}{ccc}
p^{2}-1 & 0 & -31-q^{3} \\
7 & r+1 & 9 \\
-2 & 8 & s-1
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & -4 \\
7 & \frac{3}{2} & 9 \\
-2 & 8 & -\pi
\end{array}\right]\) எனில், p, q, r, s ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு :
p² – 1 = 1
p² = 1 + 1 = 2 ⇒ p = ±√2
– 31 – q³ = -4
⇒ -q³ = -4 + 31 = 27 = 3³
⇒ q = -3
r + 1 = \(\frac{3}{2}\)
⇒ r = \(\frac{3}{2}\) – 1 = \(\frac{3-2}{2}=\frac{1}{2}\)
s – 1 = -π
s = -π + 1 = 1 – π
∴ p = ±√2, q = -3, r = \(\frac{1}{2}\), s = 1 – π.

Question 3.
\(\left[\begin{array}{cc}
2 x+y & 4 x \\
5 x-7 & 4 x
\end{array}\right]=\left[\begin{array}{cc}
7 & 7 y-13 \\
y & x+6
\end{array}\right]\) எனில், x + y ஐ காண்க.
தீர்வு :
2x + y = 7 …… (1)
7y – 13 = 4x
⇒ 4x – 7y = -13 ………… (2)

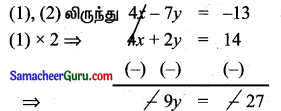
y = \(\frac{27}{9}\) = 3
y = 3 என (1)-ல் பிரதியிட,
2x + 3 = 7 ⇒ 2x = 7 – 3 = 4
x = 2
∴ x + y = 2 + 3 = 5

Question 4.
2A – B = \(\left[\begin{array}{rrr}
6 & -6 & 0 \\
-4 & 2 & 1
\end{array}\right]\) = 0 மற்றும்
A – 2B = \(\left[\begin{array}{rrr}
3 & 2 & 8 \\
-2 & 1 & -7
\end{array}\right]\) என்ற அணிச்சமன்பாடுகளை நிறைவு செய்யும், A, B என்ற அணிகளைக் காண்க.
தீர்வு:
A – 2B = \(\left[\begin{array}{rrr}
3 & 2 & 8 \\
-2 & 1 & -7
\end{array}\right]\) ……(1)

2A – B =\(\left[\begin{array}{rrr}
6 & -6 & 0 \\
-4 & 2 & 1
\end{array}\right]\) ……(2)

Question 5.
A = \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\) எனில், A⁴ -இ காண்க
தீர்வு:
A = \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\)
⇒ A⁴ = AAAA
= \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\)

A² = \(\left(\begin{array}{cc}
1 & a \\
0 & 1
\end{array}\right)\left(\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right)\)
= \(\left[\begin{array}{ll}
(1 \times 1+a \times 0) & (1 \times a+a \times 1) \\
(0 \times 1+1 \times 0) & (0 \times a+1 \times 1)
\end{array}\right]\)
= \(\left[\begin{array}{cc}
(1+0) & (a+a) \\
(0+0) & (0+1)
\end{array}\right]=\left[\begin{array}{cc}
1 & 2 a \\
0 & 1
\end{array}\right]\)

A⁴ = A² A²
= \(\left[\begin{array}{cc}
1 & 2 a \\
0 & 1
\end{array}\right]\left[\begin{array}{cc}
1 & 2 a \\
0 & 1
\end{array}\right]\)
= \(\left[\begin{array}{rr}
((1 \times 1)+(2 a \times 0)) & (2 a+2 a) \\
(0+0) & (0+1)
\end{array}\right]\)
∴ A⁴ = \(\left[\begin{array}{cc}
1 & 4 a \\
0 & 1
\end{array}\right]\)

Question 6.
A_α = \(\left[\begin{array}{ll}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) எனில்,
(i) A_αA_β = A_α+β என நிறுவுக.
(ii) A_α + A_α^T = I என்ற நிபந்தனையை நிறைவு செய்யும் என் அனைத்து மெய் மதிப்புகளையும் காண்க.
தீர்வு:
(i) A_α = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)

A_β = \(\left[\begin{array}{cc}
\cos \beta & -\sin \beta \\
\sin \beta & \cos \beta
\end{array}\right]\)

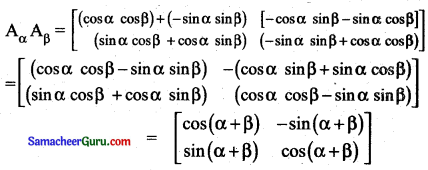
(ii) A_α + A_α^T = I
A_α = \(\left[\begin{array}{ll}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)

A_α^T = \(\left[\begin{array}{rr}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)

A_α + A_α^T = \(\left[\begin{array}{rr}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]+\left[\begin{array}{rr}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)
= \(\left[\begin{array}{cc}
2 \cos \alpha & 0 \\
0 & 2 \cos \alpha
\end{array}\right]=\mathrm{I}=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)

2 cos α = 1
⇒ cos α = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
⇒ α = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z

Question 7.
A = \(\left[\begin{array}{rr}
4 & 2 \\
-1 & x
\end{array}\right]\) மற்றும் (A – 2I) (A – 3I) = 0 எனில், ன் மதிப்பைக் காண்க.
தீர்வு:
(A – 2I) = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & x
\end{array}\right]-2\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]\)
= \(\left(\begin{array}{cc}
4 & 2 \\
-1 & x
\end{array}\right)-\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]=\left[\begin{array}{cc}
2 & 2 \\
-1 & x-2
\end{array}\right]\)

(A – 3I) = \(\left(\begin{array}{cc}
4 & 2 \\
-1 & x
\end{array}\right)-3\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)
= \(\left(\begin{array}{cc}
4 & 2 \\
-1 & x
\end{array}\right)-\left(\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right)=\left(\begin{array}{rr}
1 & 2 \\
-1 & x-3
\end{array}\right)\)
(A – 2I) (A – 3I) = \(\left(\begin{array}{rr}
2 & 2 \\
1 & x-2
\end{array}\right)\left(\begin{array}{cc}
1 & 2 \\
-1 & x-3
\end{array}\right)\) = 0 என தரப்பட்டுள்ளது.

\(\left[\begin{array}{rr}
(2-2) & 4+(2 x-6) \\
1-(x-2) & 2+(x-2)(x-3)
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

4 + 2x – 6 = 0
2x – 2 = 0
x = 1

Question 8.
A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\) எனில், A² என்பது அலகு அணியாகும் என நிறுவுக.
தீர்வு :
A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\)

A² = A.A = \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\) \(\left[\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\)
= \(\left[\begin{array}{ccc}
1+0+0 & 0+0+0 & 0+0+0 \\
0+0+0 & 0+1+0 & 0+0+0 \\
a+0-a & 0+b-b & 0+0+1
\end{array}\right]\)

= \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I எனவே நிருபிக்கப்பட்டது.

Question 9.
A = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\) மற்றும் A³ – 6A² + 7A + kI = 0, எனில், k -ஐ காண்க.
தீர்வு :
A = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\)

A³ = AAA
A² = AA = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\)
= \(\left[\begin{array}{lll}
(1+0+4) & (0+0+0) & (2+0+6) \\
(0+0+2) & (0+4+0) & (0+2+3) \\
(2+0+6) & (0+0+0) & (4+0+9)
\end{array}\right]=\left[\begin{array}{ccc}
5 & 0 & 8 \\
2 & 4 & 5 \\
8 & 0 & 13
\end{array}\right]\)
A³ = A²A = \(\left[\begin{array}{ccc}
5 & 0 & 8 \\
2 & 4 & 5 \\
8 & 0 & 13
\end{array}\right]\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\)

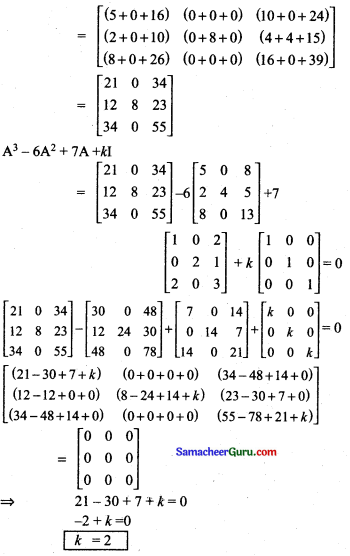
Question 10.
பின்வரும் நிபந்தனைகள் ஒவ்வொன்றையும் நிறைவு செய்யும் அணிகளுக்கான எடுத்துக்காட்டுகளைத் தருக.
(i) AB ≠ BA எனுமாறுள்ள A மற்றும் B அணிகள்.
(ii) AB = 0 = BA, A # 0 மற்றும் B ≠ 0 எனுமாறுள்ள A, B அணிகள்.
(ii) AB = 0 மற்றும் BA ≠ 0 எனுமாறுள்ள A, B அணிகள்
தீர்வு :
AB ≠ BA
(i) A = \(\left[\begin{array}{rr}
1 & 2 \\
0 & -1
\end{array}\right]\), B = \(\left[\begin{array}{rr}
2 & 1 \\
-1 & 0
\end{array}\right]\)
AB = \(\left[\begin{array}{rr}
1 & 2 \\
0 & -1
\end{array}\right]\left[\begin{array}{rr}
2 & 1 \\
-1 & 0
\end{array}\right]=\left[\begin{array}{cc}
(2-2) & (1+0) \\
(0+1) & (0+0)
\end{array}\right]\)
= \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) …………(1)

(iii)

Question 11.
f(x) = \(\left[\begin{array}{rrr}
\cos x & -\sin x & 0 \\
\sin x & \cos x & 0 \\
0 & 0 & 1
\end{array}\right]\), எனில், f(x)f(y) = f(x + y) என நிறுவுக.
தீர்வு :
f(x) . f(y) = \(\left[\begin{array}{rrr}
\cos x & -\sin x & 0 \\
\sin x & \cos x & 0 \\
0 & 0 & 1
\end{array}\right]\) \(\left[\begin{array}{rrr}
\cos y & -\sin y & 0 \\
\sin y & \cos y & 0 \\
0 & 0 & 1
\end{array}\right]\)
= \(\left[\begin{array}{c}
(\cos x \cos y-\sin x \sin y+0) \\
(\sin x \cos y+\cos x \sin y+0) \\
(0+0+0)
\end{array}\right.\)
\( \left.\begin{array}{cc}
(-\cos x \sin y-\sin x \cos y+0) & (0+0+0) \\
(-\sin x \sin y+\cos x \cos y+0) & (0+0+0) \\
(0+0+0) & (0+0+1)
\end{array}\right]\)
= \(\left[\begin{array}{ccc}
\cos (x+y) & -\sin (x+y) & 0 \\
\sin (x+y) & \cos (x+y) & 0 \\
0 & 0 & 1
\end{array}\right]\)
= f(x+y)
எனவே f (x) f (y) = f (x+y) என நிருபிக்கப்பட்டது.

Question 12.
A என்பது A² = A என்றவாறுள்ள ஒரு சதுர அணி எனில், 7A – (I + A)³ -ன் மதிப்புக் காண்க. தீர்வு :
7A – (I + A)³ = 7A [I³ + A³ + 3A (I + A)]
= 7A – [I + A + 3A + 3A]
= 7A – [I + 7A]
=
= -I

Question 13.
A = \(\left[\begin{array}{rrr}
2 & 0 & -3 \\
1 & 4 & 5
\end{array}\right]\), B = \(\left[\begin{array}{rr}
3 & 1 \\
-1 & 0 \\
4 & 2
\end{array}\right]\)எனில், C = \(\left[\begin{array}{rr}
4 & 7 \\
2 & 1 \\
1 & -1
\end{array}\right]\)
[1 -1] எனில், A(B + C) = AB + AC, எனும் பண்பினைச் சரிபார்க்க.
தீர்வு :

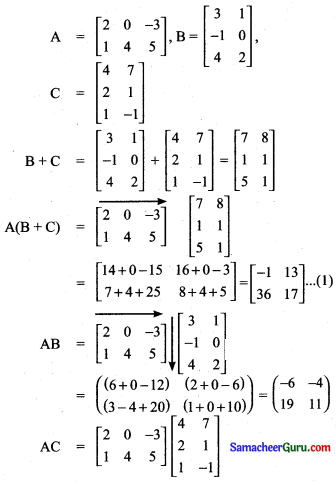
= \(\left(\begin{array}{cc}
(8+0-3) & (14+0+3) \\
(4+8+5) & (7+4-5)
\end{array}\right)=\left[\begin{array}{cc}
5 & 17 \\
17 & 6
\end{array}\right]\)

AB + AC = \(\left(\begin{array}{cc}
-6 & -4 \\
19 & 11
\end{array}\right)+\left[\begin{array}{cc}
5 & 17 \\
17 & 6
\end{array}\right]=\left[\begin{array}{cc}
-1 & 13 \\
36 & 17
\end{array}\right]\) ……..(2)
(1) = (2)
∴ A(B + C) = AB + AC என்பது சரிபார்க்கப்பட்டது.

Question 14.
A\(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]=\left[\begin{array}{rrr}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\) என்ற அணிய சமன்பாட்டினை நிறைவு செய்யும் A என்ற அணியைக் காண்க.
தீர்வு :
A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]\) என்க.

\(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]=\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

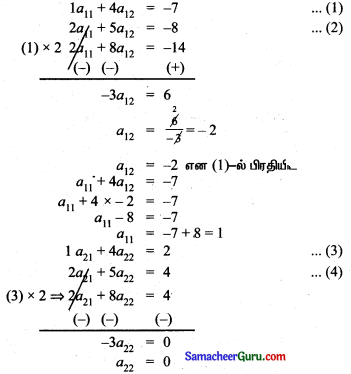
a₂₂ = 0 என (3)ல் பிரதியிட
1a₂₁ + 4 × 0 = 2 ……(3)
a₂₁ = 2 ……(4)
∴ A = \(\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)=\left(\begin{array}{rr}
1 & -2 \\
2 & 0
\end{array}\right)\)

Question 15.
A^T = \(\left[\begin{array}{rr}
4 & 5 \\
-1 & 0 \\
2 & 3
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
7 & 5 & -2
\end{array}\right]\) பின்வருவனவற்றைச் சரிபார்க்க.
(i) (A + B)^T = A^T + B^T = B^T + A^T
(ii) (A – B)^T = A^T – B^T
(iii) (B^T)^T = B.
தீர்வு :
(i) A = \(\left[\begin{array}{ccc}
4 & -1 & 2 \\
5 & 0 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
7 & 5 & -2
\end{array}\right]\)

(A + B) = \(\left[\begin{array}{lll}
(4+2) & (-1-1) & (2+1) \\
(5+7) & (0+5) & (3-2)
\end{array}\right]\) = \(\left[\begin{array}{ccc}
6 & -2 & 3 \\
12 & 5 & 1
\end{array}\right]\)

(A + B)^T = \(\left[\begin{array}{cc}
6 & 12 \\
-2 & 5 \\
3 & 1
\end{array}\right]\) ……….(1)

B^T = \(\left[\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right]\)

A^T + B^T = \(\left[\begin{array}{cc}
4 & 5 \\
-1 & 0 \\
2 & 3
\end{array}\right]+\left[\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right]\)
= \(\left[\begin{array}{cc}
6 & 12 \\
-2 & 5 \\
3 & 1
\end{array}\right]\) ………..(2)

B^T + A^T = \(\left[\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right]+\left[\begin{array}{cc}
4 & 5 \\
-1 & 0 \\
2 & 3
\end{array}\right]\)
= \(\left[\begin{array}{cc}
6 & 12 \\
-2 & 5 \\
3 & 1
\end{array}\right]\) ………(3)
(1) = (2) = (3)
∴ எனவே (A + B)^T = A^T + B^T = B^T + A^T என நிருபிக்கப்பட்டது.

(ii) ( A- B)^T = \(\left[\left(\begin{array}{rrr}
4 & -1 & 2 \\
5 & 0 & 3
\end{array}\right)-\left(\begin{array}{rrr}
2 & -1 & 1 \\
7 & 5 & -2
\end{array}\right)\right]^{\mathrm{T}}\)
= \(\left[\begin{array}{rrr}
(4-2) & -1-(-1) & (2-1) \\
(5-7) & (0-5) & (3-(-2))
\end{array}\right]^{\mathrm{T}}\)
= \(\left(\begin{array}{rrr}
2 & 0 & 1 \\
-2 & -5 & 5
\end{array}\right)^{\mathrm{T}}=\left(\begin{array}{lr}
2 & -2 \\
0 & -5 \\
1 & 5
\end{array}\right)\) ……….(1)

A^T – B^T = \(\left[\begin{array}{cc}
4 & 5 \\
-1 & 0 \\
2 & 3
\end{array}\right]-\left[\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right]\)
= \(\left[\begin{array}{cc}
2 & -2 \\
0 & -5 \\
1 & 5
\end{array}\right]\) ……….(2)
(1) = (2)
∴ (A – B)^T = A^T – B^T என நிருபிக்கப்பட்டது.

(iii) (B^T)^T = B
B^T = \(\left(\begin{array}{rrr}
2 & -1 & 1 \\
7 & 5 & -2
\end{array}\right)^{\mathrm{T}}=\left(\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right)\)
(B^T)^T = \(\left(\begin{array}{cc}
2 & 7 \\
-1 & 5 \\
1 & -2
\end{array}\right)^{\mathrm{T}}=\left(\begin{array}{ccc}
2 & -1 & 1 \\
7 & 5 & -2
\end{array}\right)\) = B எனவே நிருபிக்கப்பட்டது.

Question 16.
3 × 4 வரிசை உடைய ஒரு அணி A மற்றும் B என்ற இரண்டு அணிகளும் A^TB மற்றும் BA^T ஆகிய இரண்டையும் வரையறை செய்யுமாறுள்ள அணிகள் எனில், B அணியின் வரிசையைக் காண்க.
தீர்வு :
A = [a_ij]_{3 × 4}
A^T = [a_ij]_{4 × 3}
B = [b_ij]_{x × y} என்க
A^TB = [a_ij]_{4 × 3} [b_ij]_{x × y}
∴ x = 3
BA^T = [b_ij]_{x × y} [a_ij]_{4 × 3}
∴ y = 4
∴ B-ன் வரிசை x × y = 3 × 4

Question 17.
பின்வரும் அணிகளை சமச்சீர் மற்றும் எதிர் சமச்சீர் ! அணிகளின் கூடுதலாக எழுதுக.
(i) \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\) (ii) \(\left[\begin{array}{rrr}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\).
தீர்வு :
(i) A = \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\) ⇒ A^T = \(\left[\begin{array}{cc}
4 & 3 \\
-2 & -5
\end{array}\right]\)

A + A^T = \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\) + \(\left[\begin{array}{cc}
4 & 3 \\
-2 & -5
\end{array}\right]\) = \(\left[\begin{array}{rr}
8 & 1 \\
1 & -10
\end{array}\right]\)
P = \(\frac{1}{2}\)(A + A^T) = \(\frac{1}{2}\) \(\left[\begin{array}{rr}
8 & 1 \\
1 & -10
\end{array}\right]\) என்க.

இப்பொழுது P^T = \(\frac{1}{2}\) \(\left[\begin{array}{rr}
8 & 1 \\
1 & -10
\end{array}\right]\) = P
ஆகையால் P = \(\frac{1}{2}\) [A + A^T] ஒரு சமச்சீர் அணியாகும்.

Q = \(\frac{1}{2}\) [A – A^T] என்க.
= \(\frac{1}{2}\) \(\left(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]-\left[\begin{array}{cc}
4 & 3 \\
-2 & -5
\end{array}\right]\right)\)
= \(\frac{1}{2}\) \(\left[\begin{array}{cc}
0 & -5 \\
5 & 0
\end{array}\right]\)
Q^T = \(\frac{1}{2}\) \(\left[\begin{array}{cc}
0 & 5 \\
-5 & 0
\end{array}\right]\) = -Q
ஆகையால் Q = \(\frac{1}{2}\) [A – A^T] எதிர் சமச்சீர் அணியாகும்.
A = P + Q
= \(\frac{1}{2}\left[\begin{array}{rr}
8 & 1 \\
1 & -10
\end{array}\right]+\frac{1}{2}\left[\begin{array}{cc}
0 & -5 \\
5 & 0
\end{array}\right]\)
ஆகவே A என்பதை சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளின் கூடுதலாக எழுதலாம்.

(ii) 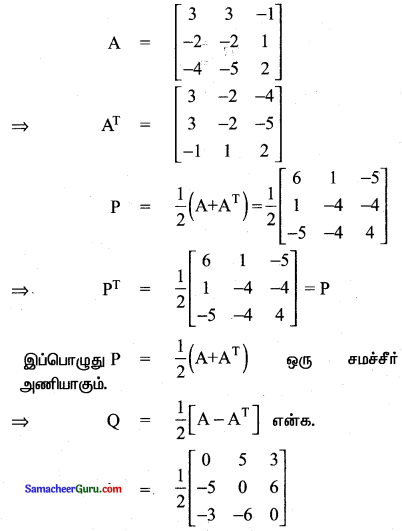ஒரு
Q^T = \(\frac{1}{2}\)\(\left[\begin{array}{ccc}
0 & -5 & -3 \\
5 & 0 & -6 \\
3 & 6 & 0
\end{array}\right]\) = -Q
ஆகையால் Q = \(\frac{1}{2}\) [A – A^T] எதிர் சமச்சீர் அணியாகும்.
⇒ A = P + Q = \(\frac{1}{2}\) \(\left[\begin{array}{ccc}
6 & 1 & -5 \\
1 & -4 & -4 \\
-5 & -4 & 4
\end{array}\right]\) + \(\frac{1}{2}\) \(\left[\begin{array}{ccc}
0 & 5 & 3 \\
-5 & 0 & 6 \\
-3 & -6 & 0
\end{array}\right]\)
ஆகையால் A என்பதை ஒரு சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளின் கூடுதலாக எழுதலாம்.

Question 18.
\(\left[\begin{array}{rr}
2 & -1 \\
1 & 0 \\
-3 & 4
\end{array}\right]\) A^T = \(\left[\begin{array}{rrr}
-1 & -8 & -10 \\
1 & 2 & -5 \\
9 & 22 & 15
\end{array}\right]\) எனுமாறுள்ள A என்ற அணியைக் காண்க.
தீர்வு : \(\left[\begin{array}{rr}
2 & -1 \\
1 & 0 \\
-3 & 4
\end{array}\right]\)_{3 × 2} A^T = \(\left[\begin{array}{rrr}
-1 & -8 & -10 \\
1 & 2 & -5 \\
9 & 22 & 15
\end{array}\right]\)_{3 × 3} எனில்
A^T = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right]_{2 \times 3}\) என்க.
\(\left[\begin{array}{cc}
2 & -1 \\
1 & 0 \\
-3 & 4
\end{array}\right]\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right]=\left[\begin{array}{ccc}
-1 & -8 & -10 \\
1 & 2 & -5 \\
9 & 22 & 15
\end{array}\right]\)

2a₁₁ – 1a₂₁ = -1 ………(1)
1a₁₁ + 0a₂₁ = 1 ……….(2)
1a₁₁ + 0 = 1
a₁₁ = 1
a₁₁ = 1 என (1)-ல் பிரதியிட
2 × 1 – a₂₁ = -1
-a₂₁ = -1 – 2

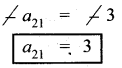
2a₁₂ – 1a₂₂ = -8 ………(3)
1a₁₂ + 0a₂₂ = 2 ………(4)
a₁₂ + 0 = 2
a₁₂ = 2 என (3)-ல் பிரதியிட
2 × 2 – a₂₂ = -8
-a₂₂ = -8 – 4 = -12
a₂₂ = 12
2a₁₃ – 1a₂₃ = -10 ……….(5)
1a₁₃ + 0a₂₃ = -5 ………..(6)
a₁₃ + 0 = -5
a₁₃ = -5 என (5)-ல் பிரதியிட
2 × -5 – a₂₃ = -10
– a₂₃ = -10 + 10 =0
a₂₃ = 0
∴ A^T = \(\left[\begin{array}{rrr}
1 & 2 & -5 \\
3 & 12 & 0
\end{array}\right]\)
∴ A = \(\left[\begin{array}{rr}
1 & 3 \\
2 & 12 \\
-5 & 0
\end{array}\right]\)

Question 19.
A = \(\left[\begin{array}{rrr}
1 & 2 & 2 \\
2 & 1 & -2 \\
x & 2 & y
\end{array}\right]\) மற்றும் AA^T = 9I எனில், x, y -ன் மதிப்புகளைக் காண்க.
தீர்வு :
AA^T = 9I
\(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
x & 2 & y
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & x \\
2 & 1 & 2 \\
2 & -2 & y
\end{array}\right]=9\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
x + 4 + 2y = 0
x + 2y = -4 ………(1)
x + 4 + 2y = 0
x + 2y = -4 ……….(2)
2x + 2 – 2y = 0

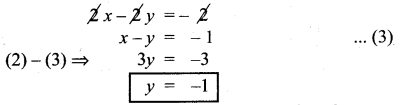
y = -1 என (1)-ல் பிரதியிட
x + 2 × -1 = – 4
x – 2 = -4
x = -4 + 2 ……….(2)
x = -2
தீர்வு : –
x = -2
y = -1

Question 20.
(i) x ன் எம்மதிப்புக்கு , A = \(\left[\begin{array}{rrr}
0 & 1 & -2 \\
-1 & 0 & x^{3} \\
2 & -3 & 0
\end{array}\right]\) யை என்பது எதிர் சமச்சீர் அணியாகும்?
(ii) \(\left[\begin{array}{ccc}
0 & p & 3 \\
2 & q^{2} & -1 \\
r & 1 & 0
\end{array}\right]\) என்பது எதிர் சமச்சீர் அணி எனில், p, q, r-ன் மதிப்புகளைக் காண்க.
தீர்வு :
A = \(\left[\begin{array}{ccc}
0 & 1 & -2 \\
-1 & 0 & x^{3} \\
2 & -3 & 0
\end{array}\right]\)

⇒ A^T = \(\left[\begin{array}{ccc}
0 & -1 & 2 \\
1 & 0 & -3 \\
-2 & x^{3} & 0
\end{array}\right]\)
A^T = -A
⇒ \(\left[\begin{array}{ccc}
0 & -1 & 2 \\
1 & 0 & -3 \\
-2 & x^{3} & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -1 & 2 \\
1 & 0 & -x^{3} \\
-2 & 3 & 0
\end{array}\right]\)
∴ x³ = 3
⇒ x = 3^{\(\frac{1}{3}\)}

(ii) A = \(\left[\begin{array}{ccc}
0 & p & 3 \\
2 & q^{2} & -1 \\
r & 1 & 0
\end{array}\right]\) என்க.
∴ A^T = \(\left[\begin{array}{ccc}
0 & 2 & r \\
p & q^{2} & 1 \\
3 & -1 & 0
\end{array}\right]\)
A^T = -A
⇒ \(\left[\begin{array}{ccc}
0 & 2 & r \\
p & q^{2} & 1 \\
3 & -1 & 0
\end{array}\right]=\left[\begin{array}{rrr}
0 & -p & -3 \\
-2 & -q^{2} & 1 \\
-r & -1 & 0
\end{array}\right]\)
p = -2
q² = -q²
⇒ 2q² = 0
q = 0
r = -3

Question 21.
a_ij = i – j எனில், A =[ a_ij]_{3 × 3}, என்ற அணியை உருவாக்குக. மேலும், A என்பது சமச்சீர் அணியா அல்லது எதிர் சமச்சீர் அணியா எனக் கூறுக.
தீர்வு :
A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
a_ij = i – j
∴ a₁₁ = 1 – 1 = 0
a₁₂ = 1 – 2 = -1
a₁₃ = 1 – 3 = -2
a₂₁ = 2 – 1 = 1
a₂₂ = 2 – 2 = 0
a₂₃ = 2 – 3 = -1
a₃₁ = 3 – 1 = 2
a₃₂ = 3 – 2 = 1
a₃₃ = 3 – 3 = 0
∴ A = \(\left[\begin{array}{ccc}
0 & -1 & -2 \\
1 & 0 & -1 \\
2 & 1 & 0
\end{array}\right]\)

⇒ A^T = \(\left[\begin{array}{ccc}
0 & 1 & 2 \\
-1 & 0 & 1 \\
-2 & -1 & 0
\end{array}\right]\) = -A
∴ A என்பது ஓர் எதிர் சமச்சீர் அணியாகும்.

Question 22.
A, B என்பன இரு சமச்சிர் அணிகள் என்க. AB = BA எனில், AB என்பது சமச்சீர் அணியாகும் என நிறுவுக. மேலும் இதன் மறுதலையும் உண்மை என நிறுவுக.
தீர்வு :
தரவு :
A = A^T, B = B^T,
AB = BA நிருபிக்க வேண்டியது :
(AB)^T = AB
நிருபணம் :
(AB)^T = B^T . A^T
[ ∴ நிரை நிரல் மாற்று விதியின் பின் திருப்புகை விதி]
= B . A [∵ B^T = B, A∵ = A]
= AB [AB = BA தரவு]
∴ (AB)^T = AB
∴ AB என்பது ஓர் சமச்சீர் அணியாகும் என்பது நிருபிக்கப்பட்டது.
மறுதலை :
தரவு :
A = A^T, B = B^T
(AB)^T = AB
நிருபணம் :
(AB)^T = B^T A^T = BA
∴ AB = BA

Question 23.
A, B என்பன சமவரிசையுள்ள இரு சமச்சீர் அணிகள் எனில், பின்வருவனவற்றை நிறுவுக.
(i) AB + BA என்பது சமச்சீர் அணியாகும்
(ii) AB – BA என்பது எதிர் சமச்சீர் அணியாகும்
தீர்வு :
தரவு : A^T = A, B^T = B
(i) (AB + BA)^T = (AB)^T + (BA)^T
= B^TA^T + A^TB^T
= BA + AB
= AB + BA
∴ AB + BA என்பது சமச்சீர் அணியாகும்.

(ii) (AB – BA)^T = (AB)^T – (BA)^T
= B^TA^T – A^TB^T
= BA – AB
= -(AB – BA)
∴ AB – BA என்பது எதிர் சமச்சீர் அணியாகும்.

Question 24.
ஓர் அங்காடியில் முந்திரி, உலர் திராட்சை மற்றும் பாதாம் பர ுப்பு ஆகியவற்றைக் கொண்டு மூன்று விதமான பரிசுப் பைகள் தயார் செய்யப்படுகின்றன. பை -ல் 100 கிராம் முந்திரி, 100 கிராம் உலர் திராட்சை மற்றும் 50 கிராம் பாதாம் பருப்பும், பை II-ல் 200 கிராம் முந்திரி, 100 கிராம் உலர் திராட்சை மற்றும் 100 கிராம் பாதாம் பருப்பும், பை III-ல் 250 கிராம் முந்திரி, 250 கிராம் உலர்திராட்சை மற்றும் 150 கிராம் பாதாம் பருப்பும் உள்ளன. .50 கிராம் முந்திரியின் விலை ₹50/-, 50 கிராம் உலர் திராட்சையின் விலை ₹10/- மற்றும் 50 கிராம் பாதாம் பருப்பின் விலை ₹60/- எனில், ஒவ்வொரு பரிசுப் பையின் விலையைக் காண்க.
தீர்வு :
பரிசுப் பைகளை ஓர் அணி வடிவில் எழுத

A = முந்திரி
உலர்ந்த திராட்சை
பாதாம் பருப்பு \(\left[\begin{array}{ccc}
\mathrm{I} & \mathrm{II} & \mathrm{III} \\
100 & 200 & 250 \\
100 & 100 & 250 \\
50 & 100 & 150
\end{array}\right]\)
k = \(\frac{1}{50}\)
விலை B = [50 10 60]
பரிசுப் பைகளின் விலை = B (kA)

= [50 10 60] \(\left(\frac{1}{50}\left[\begin{array}{ccc}
\mathrm{I} & \mathrm{II} & \mathrm{III} \\
100 & 200 & 250 \\
100 & 100 & 250 \\
50 & 100 & 150
\end{array}\right]\right)\)
BA = [50 10 60 \(\left[\begin{array}{lll}
\mathrm{I} & \mathrm{II} & \mathrm{II} \\
2 & 4 & 5 \\
2 & 2 & 5 \\
1 & 2 & 3
\end{array}\right]\)
= \(\left[\begin{array}{c}
100+20+60 \\
200+20+120 \\
250+50+180
\end{array}\right]=\left[\begin{array}{c}
180 \\
340 \\
480
\end{array}\right]\)
தீர்வு :
பை I = ₹180
பை II = ₹340
பை III = ₹ 480 ஆகும்.